C高级 框架开发中红黑树结构
引言 -- 红黑树历史
红黑树是数据结构学习中一道卡. 底层库容器中必不可少的算法. 历经各种实战运用,性能有保障. 同样红黑树不好理解, 就算理解了, 代码也不好写.
就算写了, 工程库也难构建. 关于红黑树基础讲解推荐看下面博主的红黑树博文系列,感觉不错.
对于红黑树小背景简介摘抄如下:
红黑树(英语:Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的,他称之为"对称二叉B树",它现代的名字是在Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的:它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目。
对于红黑树更加详细的历史参照下面资料.
红黑树 https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91
本文重点介绍工程开发中, 红黑树工程基库的封装.直接用现成的最爽.
前言 -- 红黑树工程库源码
一言不合就上源码!
rbtree.h
#ifndef _H_RBTREE
#define _H_RBTREE struct rbnode {
unsigned long parent_color;
struct rbnode * right;
struct rbnode * left;
}; typedef void * (* new_f)(void *);
typedef int (* cmp_f)(const void *, const void *);
typedef void (* die_f)(void *); typedef struct {
struct rbnode * root;
new_f new;
cmp_f cmp;
die_f die;
} * rbtree_t; /*
* 每个想使用红黑树的结构, 需要在头部插入下面宏.
* 例如 :
struct person {
_HEAD_RBTREE;
... // 自定义信息
};
*/
#define _HEAD_RBTREE struct rbnode __node /*
* 创建一颗红黑树头结点
* new : 注册创建结点的函数
* cmp : 注册比较的函数
* die : 注册程序销毁函数
* : 返回创建好的红黑树结点
*/
extern rbtree_t rb_new(new_f new, cmp_f cmp, die_f die); /*
* 插入一个结点, 会插入 new(pack)
* tree : 红黑树头结点
* pack : 待插入的结点当cmp(x, pack) 右结点
*/
extern void rb_insert(rbtree_t tree, void * pack); /*
* 删除能和pack匹配的结点
* tree : 红黑树结点
* pack : 当cmp(x, pack) 右结点
*/
extern void rb_remove(rbtree_t tree, void * pack); /*
* 得到红黑树中匹配的结点
* tree : 匹配的结点信息
* pack : 当前待匹配结点, cmp(x, pack)当右结点处理
*/
extern void * rb_get(rbtree_t tree, void * pack); /*
* 销毁这颗二叉树
* tree : 当前红黑树结点
*/
extern void rb_die(rbtree_t tree); #endif /* _H_RBTREE */
rbtree.c
#include "rbtree.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h> /*
* 操作辅助宏, 得到红黑树中具体父结点, 颜色. 包括详细设置信息
* r : 头结点
* p : 父结点新值
* c : 当前颜色
*/
#define rb_parent(r) ((struct rbnode *)((r)->parent_color & ~3))
#define rb_color(r) ((r)->parent_color & 1)
#define rb_is_red(r) (!rb_color(r))
#define rb_is_black(r) rb_color(r)
#define rb_set_black(r) (r)->parent_color |= 1
#define rb_set_red(r) (r)->parent_color &= ~1 static inline void rb_set_parent(struct rbnode * r, struct rbnode * p) {
r->parent_color = (r->parent_color & ) | (unsigned long)p;
} static inline void rb_set_color(struct rbnode * r, int color) {
r->parent_color = (r->parent_color & ~) | ( & color);
} static inline int _rb_cmp(const void * ln, const void * rn) {
return (const char *)ln - (const char *)rn;
} /*
* 创建一颗红黑树头结点
* new : 注册创建结点的函数
* cmp : 注册比较的函数
* die : 注册程序销毁函数
* : 返回创建好的红黑树结点
*/
rbtree_t
rb_new(new_f new, cmp_f cmp, die_f die) {
rbtree_t tree = malloc(sizeof(*tree));
if(NULL == tree) {
fprintf(stderr, "rb_new malloc is error!");
return NULL;
} tree->root = NULL;
tree->new = new;
tree->cmp = cmp ? cmp : _rb_cmp;
tree->die = die; return tree;
} static inline struct rbnode * _rb_new(rbtree_t tree, void * pack) {
struct rbnode * node = tree->new ? tree->new(pack) : pack;
memset(node, , sizeof(struct rbnode));
return node;
} /*
* 对红黑树的节点(x)进行左旋转
*
* 左旋示意图(对节点x进行左旋):
* px px
* / /
* x y
* / \ --(左旋)--> / \ #
* lx y x ry
* / \ / \
* ly ry lx ly
*
*/
static void _rbtree_left_rotate(rbtree_t tree, struct rbnode * x) {
// 设置x的右孩子为y
struct rbnode * y = x->right;
struct rbnode * xparent = rb_parent(x); // 将 “y的左孩子” 设为 “x的右孩子”;
x->right = y->left;
// 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲”
if (y->left != NULL)
rb_set_parent(y->left, x); // 将 “x的父亲” 设为 “y的父亲”
rb_set_parent(y, xparent); if (xparent == NULL)
tree->root = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
else {
if (xparent->left == x)
xparent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
else
xparent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
} // 将 “x” 设为 “y的左孩子”
y->left = x;
// 将 “x的父节点” 设为 “y”
rb_set_parent(x, y);
} /*
* 对红黑树的节点(y)进行右旋转
*
* 右旋示意图(对节点y进行左旋):
* py py
* / /
* y x
* / \ --(右旋)--> / \ #
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
static void _rbtree_right_rotate(rbtree_t tree, struct rbnode * y) {
// 设置x是当前节点的左孩子。
struct rbnode * x = y->left;
struct rbnode * yparent = rb_parent(y); // 将 “x的右孩子” 设为 “y的左孩子”;
y->left = x->right;
// 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲”
if (x->right != NULL)
rb_set_parent(x->right, y); // 将 “y的父亲” 设为 “x的父亲”
rb_set_parent(x, yparent);
if (yparent == NULL)
tree->root = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
else {
if (y == yparent->right)
yparent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子”
else
yparent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
} // 将 “y” 设为 “x的右孩子”
x->right = y;
// 将 “y的父节点” 设为 “x”
rb_set_parent(y, x);
} /*
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* tree 红黑树的根
* node 插入的结点 // 对应《算法导论》中的z
*/
static void _rbtree_insert_fixup(rbtree_t tree, struct rbnode * node) {
struct rbnode * parent, * gparent, * uncle; // 若“父节点存在,并且父节点的颜色是红色”
while ((parent = rb_parent(node)) && rb_is_red(parent)) {
gparent = rb_parent(parent); //若“父节点”是“祖父节点的左孩子”
if (parent == gparent->left) {
// Case 1条件:叔叔节点是红色
uncle = gparent->right;
if (uncle && rb_is_red(uncle)) {
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
} // Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent->right == node) {
_rbtree_left_rotate(tree, parent);
uncle = parent;
parent = node;
node = uncle;
} // Case 3条件:叔叔是黑色,且当前节点是左孩子。
rb_set_black(parent);
rb_set_red(gparent);
_rbtree_right_rotate(tree, gparent);
}
else { //若“z的父节点”是“z的祖父节点的右孩子”
// Case 1条件:叔叔节点是红色
uncle = gparent->left;
if (uncle && rb_is_red(uncle)) {
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
} // Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent->left == node) {
_rbtree_right_rotate(tree, parent);
uncle = parent;
parent = node;
node = uncle;
} // Case 3条件:叔叔是黑色,且当前节点是右孩子。
rb_set_black(parent);
rb_set_red(gparent);
_rbtree_left_rotate(tree, gparent);
}
} // 将根节点设为黑色
rb_set_black(tree->root);
} /*
* 插入一个结点, 会插入 new(pack)
* tree : 红黑树头结点
* pack : 待插入的结点当cmp(x, pack) 右结点
*/
void
rb_insert(rbtree_t tree, void * pack) {
cmp_f cmp;
struct rbnode * node, * x, * y;
if((!tree) || (!pack) || !(node = _rb_new(tree, pack))) {
fprintf(stderr, "rb_insert param is empty! tree = %p, pack = %p.\n", tree, pack);
return;
} cmp = tree->cmp;
// 开始走插入工作
y = NULL;
x = tree->root; // 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。从小到大
while (x != NULL) {
y = x;
if (cmp(x, node) > )
x = x->left;
else
x = x->right;
}
rb_set_parent(node, y); if (y != NULL) {
if (cmp(y, node) > )
y->left = node; // 情况2:若“node所包含的值” < “y所包含的值”,则将node设为“y的左孩子”
else
y->right = node; // 情况3:(“node所包含的值” >= “y所包含的值”)将node设为“y的右孩子”
}
else
tree->root = node; // 情况1:若y是空节点,则将node设为根 // 2. 设置节点的颜色为红色
rb_set_red(node); // 3. 将它重新修正为一颗二叉查找树
_rbtree_insert_fixup(tree, node);
} /*
* 红黑树删除修正函数
*
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* tree 红黑树的根
* node 待修正的节点
*/
static void _rbtree_delete_fixup(rbtree_t tree, struct rbnode * node, struct rbnode * parent) {
struct rbnode * other; while ((!node || rb_is_black(node)) && node != tree->root) {
if (parent->left == node) {
other = parent->right;
if (rb_is_red(other)) {
// Case 1: x的兄弟w是红色的
rb_set_black(other);
rb_set_red(parent);
_rbtree_left_rotate(tree, parent);
other = parent->right;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else {
if (!other->right || rb_is_black(other->right)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
rb_set_black(other->left);
rb_set_red(other);
_rbtree_right_rotate(tree, other);
other = parent->right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->right);
_rbtree_left_rotate(tree, parent);
node = tree->root;
break;
}
}
else {
other = parent->left;
if (rb_is_red(other)) {
// Case 1: x的兄弟w是红色的
rb_set_black(other);
rb_set_red(parent);
_rbtree_right_rotate(tree, parent);
other = parent->left;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else {
if (!other->left || rb_is_black(other->left)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
rb_set_black(other->right);
rb_set_red(other);
_rbtree_left_rotate(tree, other);
other = parent->left;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->left);
_rbtree_right_rotate(tree, parent);
node = tree->root;
break;
}
}
}
if (node)
rb_set_black(node);
} /*
* 删除rb_get得到的结点
* root : 红黑树结点
* pack : 当cmp(x, pack) 右结点
*/
void
rb_remove(rbtree_t tree, void * pack) {
struct rbnode * child, * parent, * node = NULL;
int color; if ((!tree) || !(node = (struct rbnode *)pack)) {
fprintf(stderr, "rb_remove check is error, tree = %p, node = %p.", tree, node);
return;
} // 被删除节点的"左右孩子都不为空"的情况。
if (NULL != node->left && node->right != NULL) {
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
struct rbnode * replace = node; // 获取后继节点
replace = replace->right;
while (replace->left != NULL)
replace = replace->left; // "node节点"不是根节点(只有根节点不存在父节点)
if ((parent = rb_parent(node))) {
if (parent->left == node)
parent->left = replace;
else
parent->right = replace;
}
else
// "node节点"是根节点,更新根节点。
tree->root = replace; // child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace->right;
parent = rb_parent(replace);
// 保存"取代节点"的颜色
color = rb_color(replace); // "被删除节点"是"它的后继节点的父节点"
if (parent == node)
parent = replace;
else {
// child不为空
if (child)
rb_set_parent(child, parent);
parent->left = child; replace->right = node->right;
rb_set_parent(node->right, replace);
} rb_set_parent(replace, rb_parent(node));
rb_set_color(replace, rb_color(node));
replace->left = node->left;
rb_set_parent(node->left, replace); if (color) // 黑色结点重新调整关系
_rbtree_delete_fixup(tree, child, parent);
// 结点销毁操作
if(tree->die)
tree->die(node);
return ;
} if (node->left !=NULL)
child = node->left;
else
child = node->right; parent = rb_parent(node);
// 保存"取代节点"的颜色
color = rb_color(node); if (child)
rb_set_parent(child, parent); // "node节点"不是根节点
if (parent) {
if (parent->left == node)
parent->left = child;
else
parent->right = child;
}
else
tree->root = child; if (!color)
_rbtree_delete_fixup(tree, child, parent);
if(tree->die)
tree->die(node);
} /*
* 得到红黑树中匹配的结点
* root : 匹配的结点信息
* pack : 当前待匹配结点, cmp(x, pack)当右结点处理
*/
void *
rb_get(rbtree_t tree, void * pack) {
cmp_f cmp;
struct rbnode * node;
if((!tree) || !pack) {
fprintf(stderr, "rb_get param is empty! tree = %p, pack = %p.\n", tree, pack);
return NULL;
} cmp = tree->cmp;
node = tree->root;
while(node) {
int ct = cmp(node, pack);
if(ct == )
return node;
node = ct > ? node->left : node->right;
} return NULL;
} // 后序遍历删除操作
static void _rb_die(struct rbnode * root, die_f die) {
if(NULL == root)
return;
_rb_die(root->left, die);
_rb_die(root->right, die);
die(root);
} /*
* 销毁这颗二叉树
* root : 当前红黑树结点
*/
void
rb_die(rbtree_t tree) {
if(!tree || !tree->root || !tree->die)
return; // 后续递归删除
_rb_die(tree->root, tree->die); // 销毁树本身内存
tree->root = NULL;
free(tree);
}
上面代码主要基于linux内核中红黑树扒下来构建的工程库. 有些细节我们简单解释一下结构. 例如
/*
* 每个想使用红黑树的结构, 需要在头部插入下面宏.
* 例如 :
struct person {
_HEAD_RBTREE;
... // 自定义信息
};
*/
#define _HEAD_RBTREE struct rbnode __node
等同于'继承'用法, 放在没一个希望用在红黑树结构的头部. 这些都是从linux内核结构中学到的技巧. libuv框架中也常用这种技巧.
也是C开发中通用潜规则! 还有一个技巧, 如下
struct rbnode {
unsigned long parent_color;
struct rbnode * right;
struct rbnode * left;
};
#define rb_parent(r) ((struct rbnode *)((r)->parent_color & ~3))
#define rb_color(r) ((r)->parent_color & 1)
也是在看内核源码中学到的技巧, 将指针的后2位地址, 用于保存结点颜色. 为什么可行呢,
因为 struct rbnode 结构体内存是以 sizeof (unsigned long) 大小对齐. 那么该结构地址也是以 n*sizeof(unsigned long) 递增.
后两位都是0空出来的. 用于保存红黑树结点的颜色信息(RED | BLACK). 不得不佩服linux内核代码的精巧.
后面还有一个自己补充的技巧
typedef void * (* new_f)(void *);
typedef int (* cmp_f)(const void *, const void *);
typedef void (* die_f)(void *); typedef struct {
struct rbnode * root;
new_f new;
cmp_f cmp;
die_f die;
} * rbtree_t;
实现注册, 创建, 比较, 销毁行为函数, 方便使用. 采用匿名结构, 也是一个C中开发一个小技巧, 这个结构只能是堆上创建. 对外可见, 但是不可构建.
后面会基于这个红黑树基础库, 构建一个简繁对照字典. 最后重申一下, 红黑树是软件开发层最后的堡垒. 数据结构算法也就到这了.

正文 -- 简单分析设计和测试
C的设计, 主要看结构. 同样C的难点也是结构. 后面我们做一个简单的简繁转换的字典, 通过C.
需要的资源见这个文件 http://files.cnblogs.com/files/life2refuel/C%E9%AB%98%E7%BA%A7%E5%B7%A5%E7%A8%8B%E4%B8%AD%E4%BD%BF%E7%94%A8%E7%BA%A2%E9%BB%91%E6%A0%91%E5%9F%BA%E5%BA%93.zip
简繁变换的词典,window上截图如下
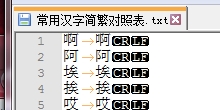
采用的是ascii编码, 这里一个汉字2字节表示. 上传到linux上后, 采用utf-8编码, 一个中文3个字节. 需要小心!
词典主程序 main.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "rbtree.h" #define _STR_PATH "常用汉字简繁对照表.txt" #define _INT_DICT (4) struct dict {
_HEAD_RBTREE; char key[_INT_DICT];
char value[_INT_DICT];
}; // 需要注册的内容
static void * _dict_new(void * arg) {
struct dict * node = malloc(sizeof(struct dict));
if (NULL == node) {
fprintf(stderr, "_dict_new malloc is error!\n");
return NULL;
} *node = *(struct dict *)arg;
return node;
} static inline int _dict_cmp(const void * ln , const void * rn) {
return strcmp(((const struct dict *)ln)->key, ((const struct dict *)rn)->key);
} static inline void _dict_die(void * arg) {
free(arg);
} // 创建内容
void dict_create(rbtree_t tree);
// 得到内容
const char * dict_get(rbtree_t tree, const char * key); /*
* 这里测试字典数据, 通过红黑树库
*/
int main(int argc, char * argv[]) {
// 创建字典树, 再读取内容
rbtree_t tree = rb_new(_dict_new, _dict_cmp, _dict_die);
if (NULL == tree) {
fprintf(stderr, "main rb_new rb is error!\n");
return -;
} // 为tree填充字典数据
dict_create(tree); // 我们输出一下 '你好'
printf("你好吗 -> %s%s%s\n",
dict_get(tree, "你"),
dict_get(tree, "好"),
dict_get(tree, "吗")
); // 字典书删除
rb_die(tree); getchar();
return ;
} // 创建内容
void
dict_create(rbtree_t tree) {
char c;
struct dict kv;
// 打开文件内容
FILE * txt = fopen(_STR_PATH, "rb");
if (NULL == txt) {
fprintf(stderr, "main fopen " _STR_PATH " rb is error!\n");
return;
} while ((c = fgetc(txt))!=EOF) {
memset(&kv, , sizeof kv);
// 读取这一行key, 并设值
kv.key[] = c;
kv.key[] = fgetc(txt); // 去掉\\t
c = fgetc(txt);
if(c < ) {
kv.key[] = c;
fgetc(txt);
} // 再设置value
kv.value[] = fgetc(txt);
kv.value[] = fgetc(txt); c = fgetc(txt);
if (c != '\r') {// 这些SB的代码, 都是解决不同系统版本的编码冲突的
kv.value[2] = c;
fgetc(txt);
} // 去掉\n
fgetc(txt); // 插入数据
rb_insert(tree, &kv);
} // 合法读取内容部分
fclose(txt);
} // 得到内容
const char *
dict_get(rbtree_t tree, const char * key) {
struct dict kv;
strncpy(kv.key, key, sizeof(kv.key) / sizeof(char));
struct dict * pkv = rb_get(tree, &kv);
return pkv ? pkv->value : NULL;
}
先看 window上测试结果
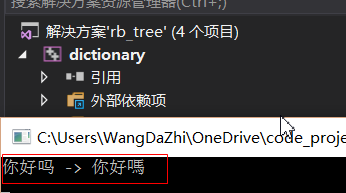
上面关于 dict_create 关于配置文件解析, 采用最原始的编码字符数解析的.
linux上 测试过程如下


linux上测试结果很正常. 到这里, 红黑树基库demo演示完毕. 也许你觉得好复杂, 但是已经很简单了. 因为C程序一个要求就是,
你需要懂得实现. 才能运用流畅. 一切都是钻木取火, 自生自灭.
扯一点, C要是有那种万能数据结构 array 或者 table 那生产率预估会提升10倍. 写代码就和玩似的.
今天完工等价于C基础数据结构已经全线通工了. C的代码写的越多, 越发觉得喜欢就好!
后记 -- 一些客气话
错误是难免的, 欢迎指正交流提高.
回家 http://music.163.com/#/song?id=157336

C高级 框架开发中红黑树结构的更多相关文章
- Vuejs+elementUI框架开发的项目结构及文件关系
项目结构|----- build #webpack编译相关文件目录,一般不用动 |----- config #配置目录| |------ dev.env.js #开发环境变量| |-- ...
- YII框架开发一个项目的通用目录结构
YII框架开发一个项目的通用目录结构: 3 testdrive/ 4 index.php Web 应用入口脚本文件 5 assets/ 包含公开的资源文件 6 css/ 包含 CSS 文件 7 ima ...
- 手写SpringMVC框架(二)-------结构开发设计
续接前文, 手写SpringMVC框架(一)项目搭建 本节我们来开始手写SpringMVC框架的第二阶段:结构开发设计. 新建一个空的springmvc.properties, 里面写我们要扫描的包名 ...
- 基于Typecho CMS框架开发大中型应用
基于Typecho CMS框架开发大中型应用 大中型应用暂且定义为:大于等于3个数据表的应用!汗吧! Typecho原本是一款博客系统,其框架体系有别于市面上一般意义MVC框架,主体代码以自创的Wid ...
- ASP.NET MVC框架开发系列课程 (webcast视频下载)
课程讲师: 赵劼 MSDN特邀讲师 赵劼(网名“老赵”.英文名“Jeffrey Zhao”,技术博客为http://jeffreyzhao.cnblogs.com),微软最有价值专家(ASP.NET ...
- Atitit.软件开发的三层结构isv金字塔模型
Atitit.软件开发的三层结构isv金字塔模型 第一层,Implements 层,着重与功能的实现.. 第二次,spec层,理论层,设计规范,接口,等.流程.方法论 顶层,val层,价值观层,原则, ...
- 微信平台ASPX高级定制开发(一):如何使用C#建立响应微信接入和自动回复的代码
微信平台不解释了,如果不了解的百度一下下,如果不会用微信,请自宫,光盘重启电脑,打开CMD输入Format C:.网上有很多针对企业级的高级定制ASPX开发,写得草草了事,很多男人干事都草草了事,这可 ...
- Yii2.0高级框架数据库增删改查的一些操作(转)
yii2.0框架是PHP开发的一个比较高效率的框架,集合了作者的大量心血,下面通过用户为例给大家详解yii2.0高级框架数据库增删改查的一些操作 --------------------------- ...
- Ruby on Rails框架开发学习
学习地址:http://www.ixueyun.com/lessons/detail-lessonId-685.html 一.课程概述 软件开发在经历了面向过程编程的阶段,现在正大行其道的是敏捷开发, ...
随机推荐
- 【bzoj1634】[Usaco2007 Jan]Protecting the Flowers 护花 贪心
题目描述 Farmer John went to cut some wood and left N (2 <= N <= 100,000) cows eating the grass, a ...
- chrome源码之恢复上次打开的标签页的学习
startup_browser_creator_impl.cc ————————>打开任何页面或浏览器的入口函数bool StartupBrowserCreatorImpl::ProcessSt ...
- 【刷题】BZOJ 2744 [HEOI2012]朋友圈
Description 在很久很久以前,曾经有两个国家和睦相处,无忧无虑的生活着.一年一度的评比大会开始了,作为和平的两国,一个朋友圈数量最多的永远都是最值得他人的尊敬,所以现在就是需要你求朋友圈的最 ...
- Android ListView 显示多种数据类型
ListView往往可能会有不同的数据类型,单类型的数据可能运用会比较少些,这也是最近项目中的一个需求{在发送消息的时候,需要选择联系人,而联系人列表由英文字母索引+联系人组成},上一篇文章只是一个基 ...
- BZOJ3653 & 洛谷3899:谈笑风生——题解
https://www.lydsy.com/JudgeOnline/problem.php?id=3653 https://www.luogu.org/problemnew/show/P3899 设 ...
- LOJ2350:[JOI2017/2018决赛]月票购买——题解
https://loj.ac/problem/2350 比较简单的题,为什么我实现得这么sb? 第一个包其实已经给了提示(第一个包的解法就是在S->T所有最短路径上的所有点到V的最短路的最小值. ...
- HDOJ(HDU).2660 Accepted Necklace (DFS)
HDOJ(HDU).2660 Accepted Necklace (DFS) 点我挑战题目 题意分析 给出一些石头,这些石头都有自身的价值和重量.现在要求从这些石头中选K个石头,求出重量不超过W的这些 ...
- 51nod 1217 Minimum Modular(数论+暴力)
根据抽屉原理显然m>=(n-K) 于是在[n-K,max(a1..an)+1]的范围中枚举m 考虑K=0的做法... 如果a[i]≡a[j](mod m),则有m|(a[i]-a[j]),只要O ...
- 那些常用的JS命令
window.location.reload()刷新当前页面. parent.location.reload()刷新父亲对象(用于框架) opener.location.reload()刷新父窗口对象 ...
- java中静态变量与静态方法的继承(转)
总结: 1.静态变量与静态方法说继承并不确切,静态方法与变量是属于类的方法与变量.而子类也属于超类,比如说Manage extends Employee,则Manage也是一个Employee,所以子 ...
