KMP算法-->深入浅出

说明：

在网上查了各种资料，终于对KMP算法有了透彻的了解，都说KMP特简单，我咋没有察觉呢？难道是智商不在线？或许都是骗纸？

还是进入正题吧，整理整理大佬的blog

KMP算法简介：

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。

我们首先用一个图来描述kmp算法的思想。在字符串S中寻找F，当匹配到位置i时两个字符串不相等，这时我们需要将字符串T向前移动。常规方法是每次向前移动一位，但是它没有考虑前i-1位已经比较过这个事实，所以效率不高。事实上，如果我们提前计算某些信息，就有可能一次前移多位。假设我们根据已经获得的信息知道可以前移k位，我们分析移位前后的T有什么特点。我们可以得到如下的结论：

• • A段字符串是F的一个前缀。
  • B段字符串是F的一个后缀。
  • A段字符串和B段字符串相等。

所以前移k位之后，可以继续比较位置i的前提是f的前i-1个位置满足：长度为i-k-1的前缀A和后缀B相同。只有这样，我们才可以前移k位后从新的位置继续比较。

所以kmp算法的核心即是计算字符串F每一个位置之前的字符串的前缀和后缀公共部分的最大长度（不包括字符串本身，否则最大长度始终是字符串本身）。

获得F每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和字符串S比较。当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将字符串F向前移动(已匹配长度-最大公共长度)位，接着继续比较下一个位置。事实上，字符串F的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较F和S即可达到字符串f前移的目的。

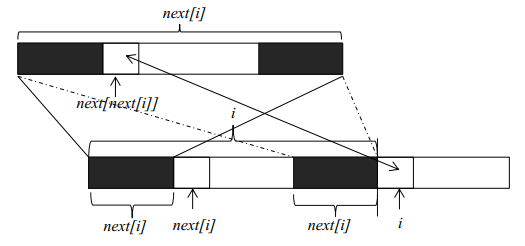
三：next数组计算：

　　理解了kmp算法的基本原理，下一步就是要获得字符串f每一个位置的最大公共长度。这个最大公共长度在算法导论里面被记为next数组。在这里要注意一点，next数组表示的是长度，下标从1开始；但是在遍历原字符串时，下标还是从0开始。假设我们现在已经求得next[1]、next[2]、……next[i]，分别表示长度为1到i的字符串的前缀和后缀最大公共长度，现在要求next[i+1]。由上图我们可以看到，如果位置i和位置next[i]处的两个字符相同（下标从零开始），则next[i+1]等于next[i]加1。如果两个位置的字符不相同，我们可以将长度为next[i]的字符串继续分割，获得其最大公共长度next[next[i]]，然后再和位置i的字符比较。这是因为长度为next[i]前缀和后缀都可以分割成上部的构造，如果位置next[next[i]]和位置i的字符相同，则next[i+1]就等于next[next[i]]加1。如果不相等，就可以继续分割长度为next[next[i]]的字符串，直到字符串长度为0为止。由此我们可以写出求next数组的代码：

void cal_next(char *str, int *next, int len)
{
    next[] = -;//next[0]初始化为-1，-1表示不存在相同的最大前缀和最大后缀
    ;//k初始化为-1
    ; q <= len-; q++)
    {
         && str[k + ] != str[q])//如果下一个不同，那么k就变成next[k]，注意next[k]是小于k的，无论k取任何值。
        {
            k = next[k];//往前回溯
        }
        ] == str[q])//如果相同，k++
        {
            k = k + ;
        }
        next[q] = k;//这个是把算的k的值（就是相同的最大前缀和最大后缀长）赋给next[q]
    }
}

四：字符串匹配

　　计算完成next数组之后，我们就可以利用next数组在字符串S中寻找字符串F的出现位置。匹配的代码和求next数组的代码非常相似，因为匹配的过程和求next数组的过程其实是一样的。假设现在字符串F的前i个位置都和从某个位置开始的字符串S匹配，现在比较第i+1个位置。如果第i+1个位置相同，接着比较第i+2个位置；如果第i+1个位置不同，则出现不匹配，我们依旧要将长度为i的字符串分割，获得其最大公共长度next[i]，然后从next[i]继续比较两个字符串。这个过程和求next数组一致，所以可以匹配代码如下：

int KMP(char *str, int slen, char *ptr, int plen)
{
    int *next = new int[plen];
    cal_next(ptr, next, plen);//计算next数组
    ;
    ; i < slen; i++)
    {
        && ptr[k + ] != str[i])//ptr和str不匹配，且k>-1（表示ptr和str有部分匹配）
            k = next[k];//往前回溯
        ] == str[i])
            k = k + ;
        )//说明k移动到ptr的最末端
        {
            //cout << "在位置" << i-plen+1<< endl;
            //k = -1;//重新初始化，寻找下一个
            //i = i - plen + 1;//i定位到该位置，外层for循环i++可以继续找下一个（这里默认存在两个匹配字符串可以部分重叠），感谢评论中同学指出错误。
            ;//返回相应的位置
        }
    }
    ;
}