codeforces 719E E. Sasha and Array(线段树)

题目链接：

E. Sasha and Array

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Sasha has an array of integers a1, a2, ..., an. You have to perform m queries. There might be queries of two types:

1. 1 l r x — increase all integers on the segment from l to r by values x;
2. 2 l r — find 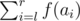, where f(x) is the x-th Fibonacci number. As this number may be large, you only have to find it modulo109 + 7.

In this problem we define Fibonacci numbers as follows: f(1) = 1, f(2) = 1, f(x) = f(x - 1) + f(x - 2) for all x > 2.

Sasha is a very talented boy and he managed to perform all queries in five seconds. Will you be able to write the program that performs as well as Sasha?

Input

The first line of the input contains two integers n and m (1 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of elements in the array and the number of queries respectively.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109).

Then follow m lines with queries descriptions. Each of them contains integers tpi, li, ri and may be xi (1 ≤ tpi ≤ 2, 1 ≤ li ≤ ri ≤ n,1 ≤ xi ≤ 109). Here tpi = 1 corresponds to the queries of the first type and tpi corresponds to the queries of the second type.

It's guaranteed that the input will contains at least one query of the second type.

Output

For each query of the second type print the answer modulo 109 + 7.

Examples

input

5 4
1 1 2 1 1
2 1 5
1 2 4 2
2 2 4
2 1 5

output

5
7
9

题意：

两个操作,1是把这个区间里的数都加x,2是求这个区间的和函数和,函数是斐波那契数列;

思路：

显然是一个线段树的题,不过维护的是矩阵,具体的可以看题解,写的太挫,跑了2000+ms;

AC代码：

#include <bits/stdc++.h>
#define lson o<<1
#define rson o<<1|1
using namespace std;
typedef long long LL;
const int maxn=1e5+10;
const LL mod=1e9+7;
LL a[maxn];
struct matrix
{
    LL a[2][2];
};
matrix add(matrix A,matrix B)
{
    matrix C;
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            C.a[i][j]=A.a[i][j]+B.a[i][j];
            if(C.a[i][j]>=mod)C.a[i][j]-=mod;
        }
    }
    return C;
}
matrix mul(matrix A,matrix B)
{
    matrix C;
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            C.a[i][j]=0;
            for(int k=0;k<2;k++)
            {
                C.a[i][j]+=A.a[i][k]*B.a[k][j];
                C.a[i][j]%=mod;
            }
        }
    }
    return C;
}
matrix pow_mod(LL x)
{
    matrix s,base;
    s.a[0][0]=s.a[1][1]=1;s.a[0][1]=s.a[1][0]=0;
    base.a[0][0]=base.a[0][1]=base.a[1][0]=1;base.a[1][1]=0;
    while(x)
    {
        if(x&1)s=mul(s,base);
        base=mul(base,base);
        x>>=1;
    }
    return s;
}

struct Tree
{
    int l,r,mark;
    matrix sum,fs;
}tr[4*maxn];

inline void pushup(int o)
{
    tr[o].sum=add(tr[lson].sum,tr[rson].sum);
}
inline void pushdown(int o)
{
    if(tr[o].mark)
    {
        tr[o].mark=0;tr[lson].mark=1;tr[rson].mark=1;
        tr[lson].sum=mul(tr[lson].sum,tr[o].fs);tr[rson].sum=mul(tr[rson].sum,tr[o].fs);
        tr[lson].fs=mul(tr[lson].fs,tr[o].fs);tr[rson].fs=mul(tr[rson].fs,tr[o].fs);
        tr[o].fs.a[0][0]=tr[o].fs.a[1][1]=1;tr[o].fs.a[1][0]=tr[o].fs.a[0][1]=0;
    }
}
void build(int o,int L ,int R)
{
    tr[o].l=L;tr[o].r=R;tr[o].mark=0;
    tr[o].fs.a[0][0]=tr[o].fs.a[1][1]=1;tr[o].fs.a[0][1]=tr[o].fs.a[1][0]=0;
    if(L>=R)
    {
        tr[o].sum=pow_mod(a[L]);
        return ;
    }
    int mid=(L+R)>>1;
    build(lson,L,mid);
    build(rson,mid+1,R);
    pushup(o);
}

LL query(int o,int L,int R)
{
    //cout<<o<<" "<<L<<" "<<R<<endl;
    if(L<=tr[o].l&&R>=tr[o].r)return tr[o].sum.a[0][0];
    int mid=(tr[o].l+tr[o].r)>>1;
    pushdown(o);
    LL ans=0;
    if(L<=mid)ans+=query(lson,L,R);
    if(R>mid)ans+=query(rson,L,R);
    pushup(o);
    return ans%mod;
}

void update(int o,int L,int R,matrix num)
{
    if(L<=tr[o].l&&R>=tr[o].r)
    {
        tr[o].fs=mul(tr[o].fs,num);
        tr[o].mark=1;
        tr[o].sum=mul(tr[o].sum,num);
        return ;
    }
    pushdown(o);
    int mid=(tr[o].l+tr[o].r)>>1;
    if(L<=mid)update(lson,L,R,num);
    if(R>mid)update(rson,L,R,num);
    pushup(o);
}
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%I64d",&a[i]),a[i]--;
    build(1,1,n);
    int op,u,v;
    LL temp;
    while(m--)
    {
        scanf("%d",&op);
        if(op==1)
        {
            scanf("%d%d%I64d",&u,&v,&temp);
            matrix num=pow_mod(temp);
            update(1,u,v,num);
        }
        else
        {
            scanf("%d%d",&u,&v);
            printf("%I64d\n",query(1,u,v));
        }
    }
    return 0;
}