『嗨威说』算法设计与分析 - PTA 程序存储问题 / 删数问题 / 最优合并问题（第四章上机实践报告）

本文索引目录：

一、PTA实验报告题1 ： 程序存储问题

　　1.1　　实践题目

　　1.2　　问题描述

　　1.3　　算法描述

　　1.4　　算法时间及空间复杂度分析

二、PTA实验报告题2 ： 删数问题

　　2.1　　实践题目

　　2.2　　问题描述

　　2.3　　算法描述

　　2.4　　算法时间及空间复杂度分析

三、PTA实验报告题3 ： 最优合并问题

　　3.1　　实践题目

　　3.2　　问题描述

　　3.3　　算法描述

　　3.4　　算法时间及空间复杂度分析

四、实验心得体会（实践收获及疑惑）

一、PTA实验报告题1 ： 程序存储问题

　　1.1　　实践题目：

　　1.2　　问题描述：

　　　　　　题意是，题干给定磁盘总容量和各个文件的占用空间，询问该磁盘最多能装几个文件。

　　1.3　　算法描述：

　　　　　　签到题，只需要将各个文件从小到大排序，并拿一个变量存储已占用的容量总和，进行对比即可得到结果。

#include<bits/stdc++.h>
#include<algorithm>
using namespace std;
#define MAXLENGTH 1000
int interger[MAXLENGTH];
int main()
{
    int num,length;
    int sum = ;
    int counter = ;
    int m = ;
    cin>>num>>length;
    for(int i=;i<num;i++){
        cin>>interger[i];
    }
    sort(interger,interger+num);
    while(true){
        if(sum+interger[m]>length||counter==num)
            break;
        sum+=interger[m];
        counter++;
        m++;
    }
    cout<<counter<<endl;
    return ;
 } 

　　1.4　　算法时间及空间复杂度分析：

　　　　　整体算法上看，输入需要O（n）的时间进行输入，最快用O（nlogn）的时间复杂度进行排序，使用O（n）的时间进行结果叠加，总时间复杂度为O（nlogn），时间复杂度花费在排序上。

　　　　空间上，只需要一个临时变量存储当前占用容量总和即可。

二、PTA实验报告题2 ： 删数问题

　　2.1　　实践题目：

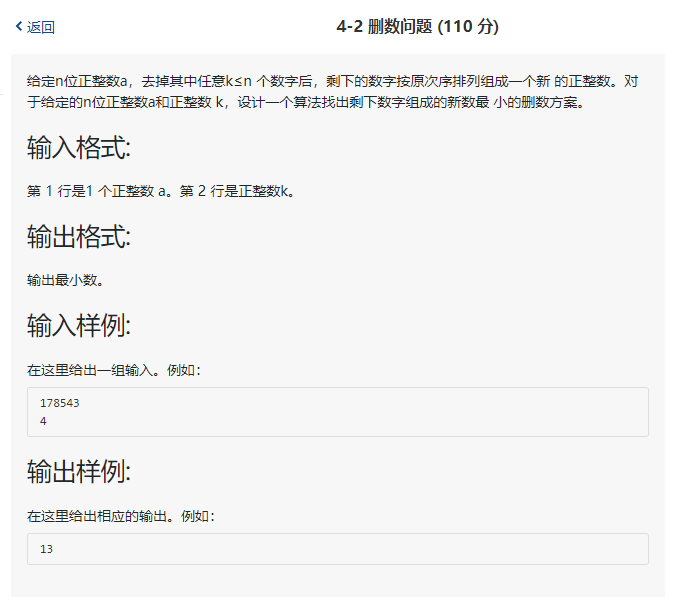
　　2.2　　问题描述：

　　　　第二题题意是指，在给定的数字串以及可删数个数的条件下，删数指定k个数，得到的数是最小的。

　　2.3　　算法描述：

　　　　首先，分析题目，删数问题，可以用一个比较方便的函数，String类的erase函数，这个函数可以删除字符串内的单个或多个字符，可以比较方便的处理删数问题。

　　　　第二，我们注意到这道题有个坑点，那就是前导零，我们需要注意100000，删除1后结果应为0

　　　　第三，确定我们的贪心策略：当当前的数，比后一位数大时，删去当前的数。

　　　　如：样例178543

　　　　用一个index时刻从头往后扫，不满足就后移。

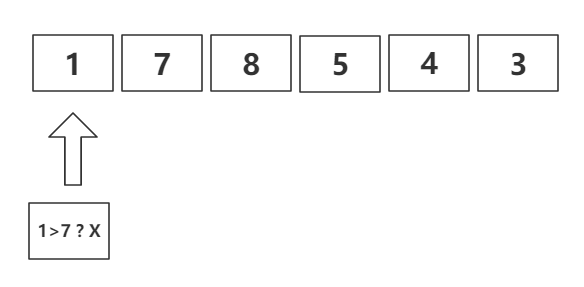
　　　　当满足之后，删除当前的值。

　　　　得到17543，这时将index重新置0，并记录已删数+1，直到满足最大删数。以此类推，直接输出string便是结果。

　　　　AC代码：

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
#define MAXLENGTH 1005
int main(){
    int k;
    string a;
    cin>>a>>k;
    int len = a.size();
    while(k>){
        for(int i = ;(i<a.size()-);i++){
            if(a[i]>a[i+])
            {
                a.erase(i,);
                break;
            }
        }
        k--;
    }
    while(a.size()>&&a[]==''){
        a.erase(,);
    }
    cout<<a<<endl;
    return ;
}

　　2.4　　算法时间及空间复杂度分析：

　　　　时间复杂度为O(n^2)，即开销在不断的删数和回溯到字符串头的过程。

　　　　空间复杂度需要一个String字符串长度，因此空间复杂度是O（n）

三、PTA实验报告题3 ： 最优合并问题

　　3.1　　实践题目：

　　3.2　　问题描述：

　　　　该题目为：题目用 2 路合并算法将这k 个序列合并成一个序列，并且合并 2 个长度分别为m和n的序列需要m+n-1 次比较，输出某段合并的最大比较次数和最小比较次数。

　　3.3　　算法描述：

　　　　这道题算是哈夫曼算法的一道裸题，很容易解决，只需要使用优秀队列不断维护最小值或最大值即可。

　　　　哈夫曼树：是一颗最优二叉树。给定n个权值作为n个叶子的结点，构造一棵二叉树，若树的带权路径长度达到最小，这棵树则被称为哈夫曼树。

　　　　因此本题根据哈夫曼算法，我们以最小比较次数为例：

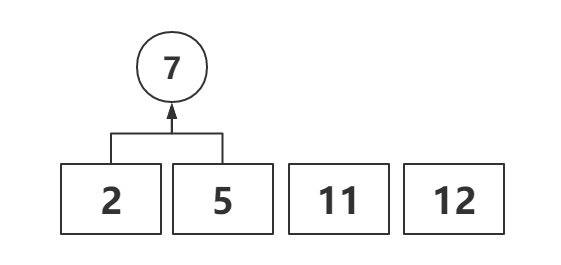
　　　　首先从队列中选出两个最小的数进行合并，并在队列中删除这两个数，并将新合成数加入队列中。

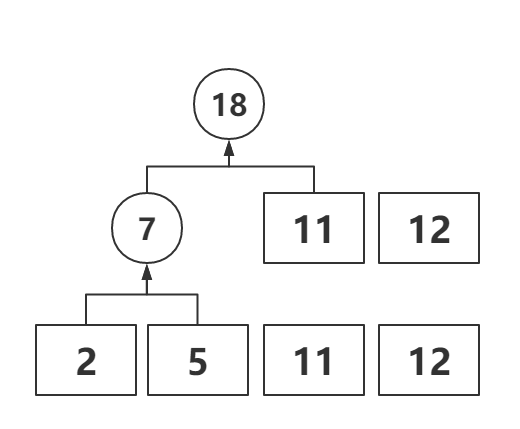
　　　　再取最小的两个数再进行合并，以此类推，得到最终的大数如下

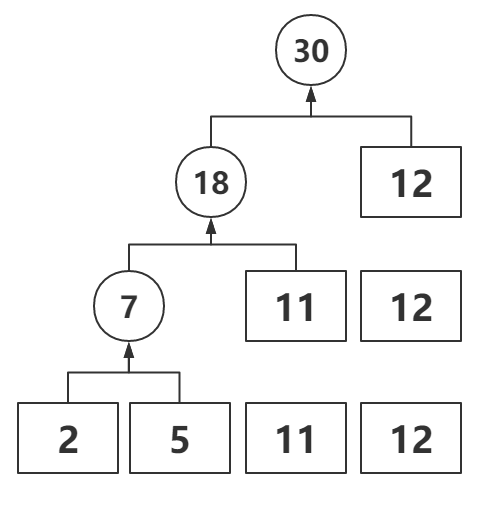
　　　　因此最小比较次数为：（ 7 - 1 ） + （ 18 - 1 ） + （ 30 - 1 ） =  52，即为所得。最大比较次数也是同理。

　　　AC代码如下：

#include<bits/stdc++.h>
using namespace std;
priority_queue<int> Haff;
priority_queue<int, vector<int>, greater<int> > Haff2;
int n,ans1,ans2;

int main()
{
    cin>>n;
    for(int i = ;i<n;i++)
    {
        int temp;
        cin>>temp;
        Haff.push(temp);
        Haff2.push(temp);
    }

    while()
    {
        if(Haff.size() == )
            break;
        int temp1 = Haff.top();
        Haff.pop();
        int temp2 = Haff.top();
        Haff.pop();
        Haff.push(temp1+temp2);
        ans1 += temp1+temp2-;
    }

    while()
    {
        if(Haff2.size() == )
            break;
        int temp1 = Haff2.top();
        Haff2.pop();
        int temp2 = Haff2.top();
        Haff2.pop();
        Haff2.push(temp1+temp2);
        ans2 += temp1+temp2-;
    }
    cout<<ans1<<" "<<ans2;
    return ;
 } 

　　3.4　　算法时间及空间复杂度分析：

　　　　由分析易知，虽然进行了两次优先队列维护，但是总的时间复杂度数量级是不变的，用O（n/2）的时间pop和push合成树。在优先队列里面用红黑树对顺序进行维护，时间复杂度为O（nlogn），最后将统计的结果输出，总的时间复杂度为O（nlogn）。

　　　空间复杂度为两棵红黑树，即T（2n） = O（n）。

四、实验心得体会（实践收获及疑惑）：

　　　　经过动态规划的肆虐之后，贪心算法变得稍微容易很多，和三木小哥哥的合作很愉快，能够很好较快及时的解决三道实践问题，暂无太多的问题，继续加油。

如有错误不当之处，烦请指正。