优先队列与TopK

一、简介

　　前文介绍了《最大堆》的实现，本章节在最大堆的基础上实现一个简单的优先队列。优先队列的实现本身没什么难度，所以本文我们从优先队列的场景出发介绍topK问题。

　　后面会持续更新数据结构相关的博文。

　　数据结构专栏：https://www.cnblogs.com/hello-shf/category/1519192.html

　　git传送门：https://github.com/hello-shf/data-structure.git

二、优先队列

　　普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

　　上面是百度百科给出的优先队列的解释。解释的还是很到位的。具体的优先队列的实现可以采用最小堆或者最大堆。因为在我们前文《最大堆》的实现中，该堆存储的元素是要求实现Comparable接口的。所以优先级是掌握在用户手中的，所以最小堆和最大堆都可以作为优先队列的底层数据结构。

　　普通的队列Queue，我们都知道是先进先出（FIFO）的，所以元素的出队顺序和入队顺序是保持一致的。但是对于我们的优先队列，出队操作，将不保证先进先出的队列特性，而是根据元素的优先级（或者说权重）决定出队的顺序。

　　如果最小元素拥有最高的优先级，那么这种优先队列叫作升序优先队列，即总是优先删除最小的元素。同理，如果最大元素拥有最高的优先级，那么这种优先队列叫作降序优先队列，即总是先删除最大的元素。

　　优先队列的使用场景：

 算法场景：
     最短路径算法：Dijkstra算法
     最小生成树算法：Prim算法
     事件驱动仿真：顾客排队算法
     选择问题：查找第k个最小元素
 实现场景：
     游戏中优先攻击最近单位，优先攻击血量最低等
     售票窗口的老幼病残孕和军人优先购票等

三、优先队列的实现

3.1、队列接口定义

　　同普通的队列，我们先定义队列的接口如下

 /**
  * 描述：队列
  *
  * @Author shf
  * @Date 2019/7/18 15:30
  * @Version V1.0
  **/
 public interface Queue<E> {
     /**
      * 获取当前队列的元素数
      * @return
      */
     int getSize();

     /**
      * 判断当前队列是否为空
      * @return
      */
     boolean isEmpty();

     /**
      * 入队操作
      * @param e
      */
     void enqueue(E e);

     /**
      * 出队操作
      * @return
      */
     E dequeue();

     /**
      * 获取队列头元素
      * @return
      */
     E getFront();
 }

　　

3.2、最大堆实现的优先队列

　　我们使用前文实现的《最大堆》来实现一个优先队列

 /**
  * 描述：优先队列
  *
  * @Author shf
  * @Date 2019/7/18 17:31
  * @Version V1.0
  **/
 public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

     private MaxHeap<E> maxHeap;

     public PriorityQueue(){
         maxHeap = new MaxHeap<>();
     }

     @Override
     public int getSize(){
         return maxHeap.size();
     }

     @Override
     public boolean isEmpty(){
         return maxHeap.isEmpty();
     }

     @Override
     public E getFront(){
         // 获取队列的头元素，在最大堆中就是获取堆顶元素
         return maxHeap.findMax();
     }

     @Override
     public void enqueue(E e){
         // 压栈 直接向最大堆中添加，让最大堆的add方法维护 元素的优先级
         maxHeap.add(e);
     }

     @Override
     public E dequeue(){
         // 出栈 将最大堆的堆顶元素取出
         return maxHeap.extractMax();
     }
 }

　　需要解释的都在代码注释中了。

　　到这里优先队列就实现完了，是不是很简单。

　　在java中也有一个类PriorityQueue，其底层是采用的最小堆实现的优先队列。在java PriorityQueue中关于优先级的定义，优先级队列的元素按照其自然顺序进行排序，或者根据构造队列时提供的 Comparator 进行排序，具体取决于所使用的构造方法。底层数据结构最大堆或者最小堆是没有什么区别的。关键在于我们如何定义优先级。

四、topK问题

　　关于topK问题，leetcode上面有一道典型的题目

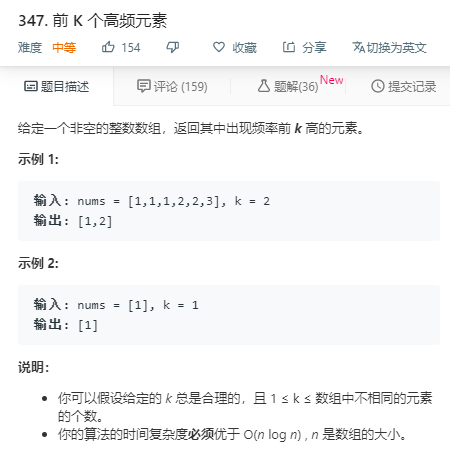
　　题目最终需要返回的是前 k 个频率最大的元素，可以想到借助堆这种数据结构，对于 k 频率之后的元素不用再去处理，进一步优化时间复杂度。

　　具体操作为：

借助 哈希表 来建立数字和其出现次数的映射，遍历一遍数组统计元素的频率
维护一个元素数目为 k 的最小堆
每次都将新的元素与堆顶元素（堆中频率最小的元素）进行比较
如果新的元素的频率比堆顶端的元素大，则弹出堆顶端的元素，将新的元素添加进堆中
最终，堆中的 k 个元素即为前 k 个高频元素

　　具体实现

 class Solution {
     public List<Integer> topKFrequent(int[] nums, int k) {
         // 使用字典，统计每个元素出现的次数，元素为键，元素出现的次数为值
         HashMap<Integer,Integer> map = new HashMap();
         for(int num : nums){
             if (map.containsKey(num)) {
                map.put(num, map.get(num) + 1);
              } else {
                 map.put(num, 1);
              }
         }
         // 遍历map，用最小堆保存频率最大的k个元素
         PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() {
             @Override
             public int compare(Integer a, Integer b) {
                 return map.get(a) - map.get(b);
             }
         });
         for (Integer key : map.keySet()) {
             if (pq.size() < k) {
                 pq.add(key);
             } else if (map.get(key) > map.get(pq.peek())) {
                 pq.remove();
                 pq.add(key);
             }
         }
         // 取出最小堆中的元素
         List<Integer> res = new ArrayList<>();
         while (!pq.isEmpty()) {
             res.add(pq.remove());
         }
         return res;
     }
 }

　　以上是使用java原生的优先队列实现的。接下来我们用我们自己实现的PriorityQueue试验一下。

　　首先因为我们没有提供接收一个Comparator的构造器，所以我们通过定义一个类来完成这个过程比较。

　　因为自己定义的优先队列底层使用的是我们自己实现的最大堆，以及最大堆底层数组也是使用自己定义的，所以我们在leetcode提交验证的时候，需要将这些自定义的类以内部类的方式提交上去。整体代码如下

 /// 347. Top K Frequent Elements
 /// https://leetcode.com/problems/top-k-frequent-elements/description/

 import java.util.LinkedList;
 import java.util.List;
 import java.util.TreeMap;

 class Solution {

     private class Array<E> {

         private E[] data;
         private int size;

         // 构造函数，传入数组的容量capacity构造Array
         public Array(int capacity){
             data = (E[])new Object[capacity];
             size = 0;
         }

         // 无参数的构造函数，默认数组的容量capacity=10
         public Array(){
             this(10);
         }

         public Array(E[] arr){
             data = (E[])new Object[arr.length];
             for(int i = 0 ; i < arr.length ; i ++)
                 data[i] = arr[i];
             size = arr.length;
         }

         // 获取数组的容量
         public int getCapacity(){
             return data.length;
         }

         // 获取数组中的元素个数
         public int getSize(){
             return size;
         }

         // 返回数组是否为空
         public boolean isEmpty(){
             return size == 0;
         }

         // 在index索引的位置插入一个新元素e
         public void add(int index, E e){

             if(index < 0 || index > size)
                 throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");

             if(size == data.length)
                 resize(2 * data.length);

             for(int i = size - 1; i >= index ; i --)
                 data[i + 1] = data[i];

             data[index] = e;

             size ++;
         }

         // 向所有元素后添加一个新元素
         public void addLast(E e){
             add(size, e);
         }

         // 在所有元素前添加一个新元素
         public void addFirst(E e){
             add(0, e);
         }

         // 获取index索引位置的元素
         public E get(int index){
             if(index < 0 || index >= size)
                 throw new IllegalArgumentException("Get failed. Index is illegal.");
             return data[index];
         }

         // 修改index索引位置的元素为e
         public void set(int index, E e){
             if(index < 0 || index >= size)
                 throw new IllegalArgumentException("Set failed. Index is illegal.");
             data[index] = e;
         }

         // 查找数组中是否有元素e
         public boolean contains(E e){
             for(int i = 0 ; i < size ; i ++){
                 if(data[i].equals(e))
                     return true;
             }
             return false;
         }

         // 查找数组中元素e所在的索引，如果不存在元素e，则返回-1
         public int find(E e){
             for(int i = 0 ; i < size ; i ++){
                 if(data[i].equals(e))
                     return i;
             }
             return -1;
         }

         // 从数组中删除index位置的元素, 返回删除的元素
         public E remove(int index){
             if(index < 0 || index >= size)
                 throw new IllegalArgumentException("Remove failed. Index is illegal.");

             E ret = data[index];
             for(int i = index + 1 ; i < size ; i ++)
                 data[i - 1] = data[i];
             size --;
             data[size] = null; // loitering objects != memory leak

             if(size == data.length / 4 && data.length / 2 != 0)
                 resize(data.length / 2);
             return ret;
         }

         // 从数组中删除第一个元素, 返回删除的元素
         public E removeFirst(){
             return remove(0);
         }

         // 从数组中删除最后一个元素, 返回删除的元素
         public E removeLast(){
             return remove(size - 1);
         }

         // 从数组中删除元素e
         public void removeElement(E e){
             int index = find(e);
             if(index != -1)
                 remove(index);
         }

         public void swap(int i, int j){

             if(i < 0 || i >= size || j < 0 || j >= size)
                 throw new IllegalArgumentException("Index is illegal.");

             E t = data[i];
             data[i] = data[j];
             data[j] = t;
         }

         @Override
         public String toString(){

             StringBuilder res = new StringBuilder();
             res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
             res.append('[');
             for(int i = 0 ; i < size ; i ++){
                 res.append(data[i]);
                 if(i != size - 1)
                     res.append(", ");
             }
             res.append(']');
             return res.toString();
         }

         // 将数组空间的容量变成newCapacity大小
         private void resize(int newCapacity){

             E[] newData = (E[])new Object[newCapacity];
             for(int i = 0 ; i < size ; i ++)
                 newData[i] = data[i];
             data = newData;
         }
     }

     private class MaxHeap<E extends Comparable<E>> {

         private Array<E> data;

         public MaxHeap(int capacity){
             data = new Array<>(capacity);
         }

         public MaxHeap(){
             data = new Array<>();
         }

         public MaxHeap(E[] arr){
             data = new Array<>(arr);
             for(int i = parent(arr.length - 1) ; i >= 0 ; i --)
                 siftDown(i);
         }

         // 返回堆中的元素个数
         public int size(){
             return data.getSize();
         }

         // 返回一个布尔值, 表示堆中是否为空
         public boolean isEmpty(){
             return data.isEmpty();
         }

         // 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
         private int parent(int index){
             if(index == 0)
                 throw new IllegalArgumentException("index-0 doesn't have parent.");
             return (index - 1) / 2;
         }

         // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
         private int leftChild(int index){
             return index * 2 + 1;
         }

         // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
         private int rightChild(int index){
             return index * 2 + 2;
         }

         // 向堆中添加元素
         public void add(E e){
             data.addLast(e);
             siftUp(data.getSize() - 1);
         }

         private void siftUp(int k){

             while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
                 data.swap(k, parent(k));
                 k = parent(k);
             }
         }

         // 看堆中的最大元素
         public E findMax(){
             if(data.getSize() == 0)
                 throw new IllegalArgumentException("Can not findMax when heap is empty.");
             return data.get(0);
         }

         // 取出堆中最大元素
         public E extractMax(){

             E ret = findMax();

             data.swap(0, data.getSize() - 1);
             data.removeLast();
             siftDown(0);

             return ret;
         }

         private void siftDown(int k){

             while(leftChild(k) < data.getSize()){
                 int j = leftChild(k); // 在此轮循环中,data[k]和data[j]交换位置
                 if( j + 1 < data.getSize() &&
                         data.get(j + 1).compareTo(data.get(j)) > 0 )
                     j ++;
                 // data[j] 是 leftChild 和 rightChild 中的最大值

                 if(data.get(k).compareTo(data.get(j)) >= 0 )
                     break;

                 data.swap(k, j);
                 k = j;
             }
         }

         // 取出堆中的最大元素，并且替换成元素e
         public E replace(E e){

             E ret = findMax();
             data.set(0, e);
             siftDown(0);
             return ret;
         }
     }

     private interface Queue<E> {

         int getSize();
         boolean isEmpty();
         void enqueue(E e);
         E dequeue();
         E getFront();
     }

     private class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

         private MaxHeap<E> maxHeap;

         public PriorityQueue(){
             maxHeap = new MaxHeap<>();
         }

         @Override
         public int getSize(){
             return maxHeap.size();
         }

         @Override
         public boolean isEmpty(){
             return maxHeap.isEmpty();
         }

         @Override
         public E getFront(){
             return maxHeap.findMax();
         }

         @Override
         public void enqueue(E e){
             maxHeap.add(e);
         }

         @Override
         public E dequeue(){
             return maxHeap.extractMax();
         }
     }

     private class Freq implements Comparable<Freq>{

         public int e, freq;

         public Freq(int e, int freq){
             this.e = e;
             this.freq = freq;
         }

         @Override
         public int compareTo(Freq another){
             if(this.freq < another.freq)
                 return 1;
             else if(this.freq > another.freq)
                 return -1;
             else
                 return 0;
         }
     }

     public List<Integer> topKFrequent(int[] nums, int k) {

         TreeMap<Integer, Integer> map = new TreeMap<>();
         for(int num: nums){
             if(map.containsKey(num))
                 map.put(num, map.get(num) + 1);
             else
                 map.put(num, 1);
         }

         PriorityQueue<Freq> pq = new PriorityQueue<>();
         for(int key: map.keySet()){
             if(pq.getSize() < k)
                 pq.enqueue(new Freq(key, map.get(key)));
             else if(map.get(key) > pq.getFront().freq){
                 pq.dequeue();
                 pq.enqueue(new Freq(key, map.get(key)));
             }
         }

         LinkedList<Integer> res = new LinkedList<>();
         while(!pq.isEmpty())
             res.add(pq.dequeue().e);
         return res;
     }

     private static void printList(List<Integer> nums){
         for(Integer num: nums)
             System.out.print(num + " ");
         System.out.println();
     }

     public static void main(String[] args) {

         int[] nums = {1, 1, 1, 2, 2, 3};
         int k = 2;
         printList((new Solution()).topKFrequent(nums, k));
     }
 }

　　在以上代码中我们需要关心的是如下部分

 　　private class Freq implements Comparable<Freq>{

         public int e, freq;

         public Freq(int e, int freq){
             this.e = e;
             this.freq = freq;
         }

         @Override
         public int compareTo(Freq another){
             if(this.freq < another.freq)
                 return 1;
             else if(this.freq > another.freq)
                 return -1;
             else
                 return 0;
         }
     }

     public List<Integer> topKFrequent(int[] nums, int k) {

         TreeMap<Integer, Integer> map = new TreeMap<>();
         for(int num: nums){
             if(map.containsKey(num))
                 map.put(num, map.get(num) + 1);
             else
                 map.put(num, 1);
         }

         PriorityQueue<Freq> pq = new PriorityQueue<>();
         for(int key: map.keySet()){
             if(pq.getSize() < k)
                 pq.enqueue(new Freq(key, map.get(key)));
             else if(map.get(key) > pq.getFront().freq){
                 pq.dequeue();
                 pq.enqueue(new Freq(key, map.get(key)));
             }
         }

         LinkedList<Integer> res = new LinkedList<>();
         while(!pq.isEmpty())
             res.add(pq.dequeue().e);
         return res;
     }

　　我们将完整代码提交到leetcode

　　得到如下结果，表示我们验证自己实现的优先队列成功了。

　　这盛世，如您所愿。

　　如有错误的地方还请留言指正。

　　原创不易，转载请注明原文地址：https://www.cnblogs.com/hello-shf/p/11397386.html