二叉查找树（查找、插入、删除）——C语言
二叉查找树
二叉查找树（BST：Binary Search Tree）是一种特殊的二叉树，它改善了二叉树节点查找的效率。二叉查找树有以下性质：
二叉查找树节点的定义：
typedef struct BSTreeNode
{
int data;
struct BSTreeNode *left;//左子树
struct BSTreeNode *right;//右子树
}BSTree;
跟普通二叉树的节点定义相同
因为查找节点和插入节点都是在已经构建好二叉查找树的前提下才能进行的，在删除节点的时候才涉及到调整二叉树的操作，所以这里先以前序遍历的顺序直接输入一个二叉查找树，代码如下
/* 创建二叉查找树（数据以前序遍历顺序输入）*/
BSTree *Create_BSTreeNode(BSTree *nod)
{
int num; scanf_s("%d", &num, );
if (num == ) /* 假定输入的数据都为正数，以0作为NULL的标志 */
{
return NULL;
}
else
{
if ((nod = (BSTree *)malloc(sizeof(BSTree))) == NULL)
{
printf("内存空间不足");
exit();
}
nod->data = num;
nod->left = Create_BSTreeNode(nod->left);
nod->right = Create_BSTreeNode(nod->right); return nod;
}
} /* 前序遍历二叉树，并打印 */
void PreOrder_Traverse(BSTree *nod, int level)
{
if (nod == NULL)
{
return ;
} printf("data = %d level = %d\n", nod->data, level);
PreOrder_Traverse(nod->left, level + );
PreOrder_Traverse(nod->right, level + );
}
1、查找节点（递归实现）
若根结点的关键字等于查找的关键字，查找成功，若小于根结点的关键字的值，递归查找左子树，若大于根结点的关键字的值，递归查找右子树，若子树为空，则查找失败，查找的操作较为简单，实现代码如下
/* 查找特定值 */
void SearchData(int targ, BSTree *nod)
{
if (nod != NULL)
{
if (nod->data == targ)
{
printf("查找值存在，值为%d\n", nod->data);
}
else if (nod->data > targ)
{
SearchData(targ, nod->left); //递归查找左子树
}
else if (nod->data < targ)
{
SearchData(targ, nod->right); //递归查找右子树
}
}
else if (nod == NULL)
{
printf("查找值不存在\n");
}
}
通过 BST 查找节点，理想情况下我们需要检查的节点数可以减半。如下图中的 BST 树，包含了 15 个节点。从根节点开始执行查找算法，第一次比较决定我们是移向左子树还是右子树，对于任意一种情况，一旦执行这一步，我们需要访问的节点数就减少了一半，从 15 降到了 7。同样，下一步访问的节点也减少了一半，从 7 降到了 3，以此类推，根据这一特点，查找算法的时间复杂度应该是 O(log2n)
（图片来源：https://www.cnblogs.com/gaochundong/p/binary_search_tree.html）
对于 BST 查找算法来说，其十分依赖于树中节点的拓扑结构，也就是节点间的布局关系，当 BST 树中的节点以扇形结构散开时，对它的插入、删除和查找操作最优的情况下可以达到亚线性的运行时间 O(log2n)，
因为当在 BST 中查找一个节点时，每一步比较操作后都会将节点的数量减少一半。尽管如此，如果拓扑结构像下图中的样子时，运行时间就会退减到线性时间 O(n)。因为每一步比较操作后还是需要逐个比较其余的节点，
也就是说，在这种情况下，在 BST 中查找节点与在数组（Array）中查找就基本类似了。
因此，BST 算法查找时间依赖于树的拓扑结构。最佳情况是 O(log2n)，而最坏情况是 O(n)
测试用例：
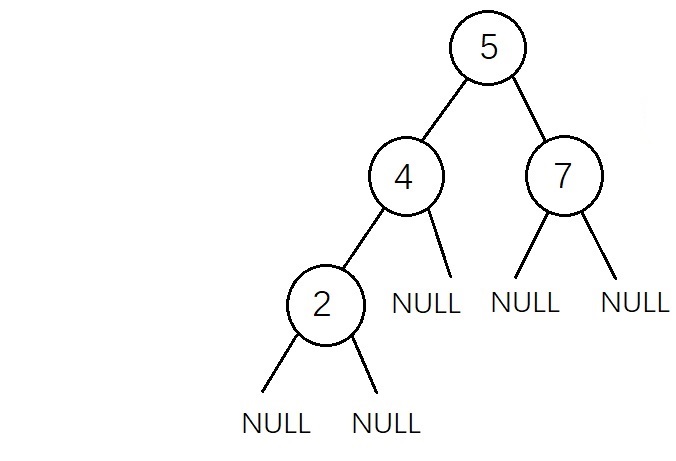
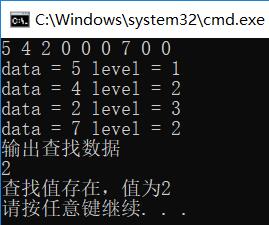
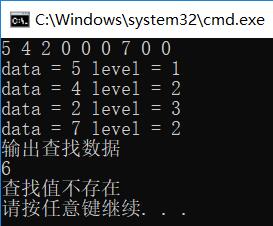
查找：以前序遍历顺序输入一个二叉查找树（0作为NULL标志）
2、插入节点（递归实现）
新插入的结点一定是一个新添加的叶子结点，如下图
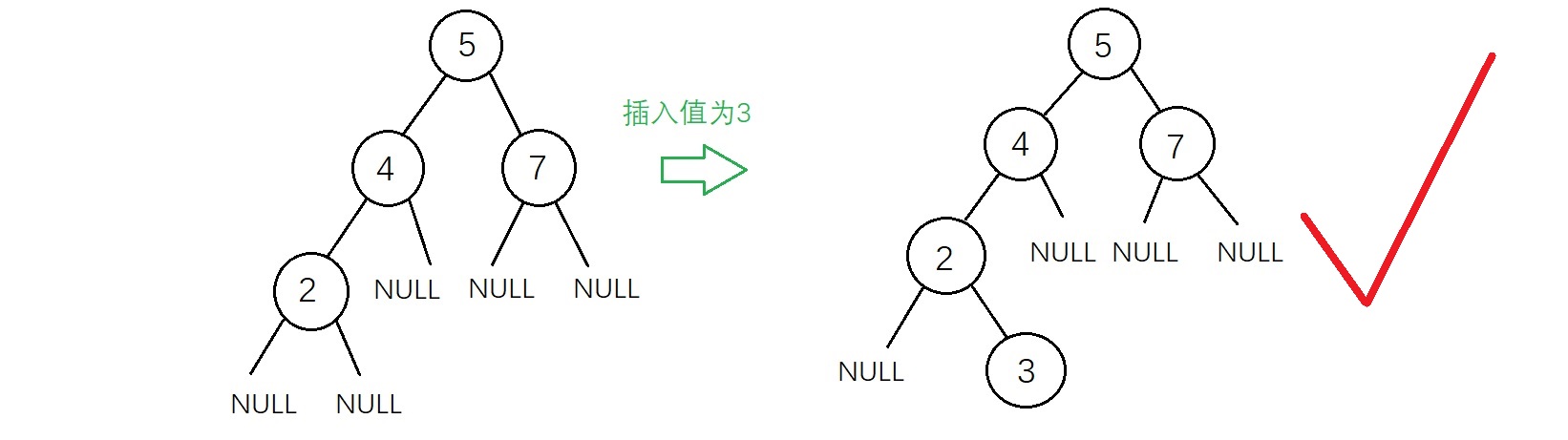
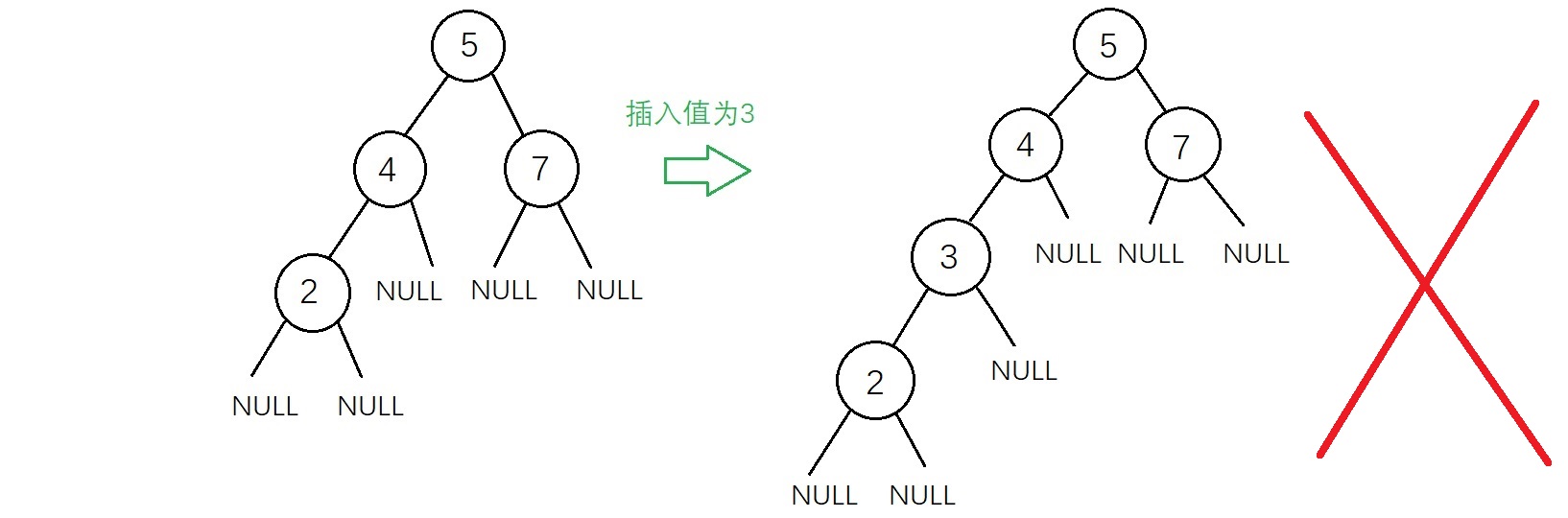
虽然上面两种插入结果得到的二叉树都符合二叉查找树的性质，但是不满足“新插入的结点一定是一个新添加的叶子结点”，因为有了这个特点插入的操作变得相对简单，实现代码如下
/* 添加新节点 */
BSTree *AddNewNode(BSTree *cur, int NewData)
{
if (cur == NULL)
{
if ((cur = (BSTree *)malloc(sizeof(BSTree))) == NULL) //创建新节点
{
printf("内存不足");
exit();
}
cur->data = NewData;
cur->left = NULL;
cur->right = NULL; return cur;
}
if (NewData > cur->data)
{
cur->right = AddNewNode(cur->right, NewData);
}
else if (NewData < cur->data)
{
cur->left = AddNewNode(cur->left, NewData);
}
else if (NewData == cur->data)
{
printf("不允许插入重复值\n");
exit();
} return cur;
}
测试用例：
插入：以前序遍历顺序输入一个二叉查找树
3、删除节点
删除节点的操作相对查找和插入要相对复杂一些，主要考虑以下三种情况（前两种情况操作较为简单，第三种较为复杂）
在删除操作前先用要找到待删除节点的位置（这里使用的递归，也可以改成迭代）
情形一：删除叶子节点
因为删除叶子节点不会破坏BST的结构，删除叶子节点的操作较为简单，步骤如下
1、判断待删除节点的左右子树是否为空，如果都为空那么就是叶子节点
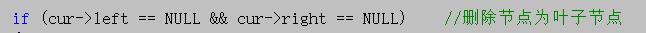
2、判断待删除节点是待删除节点父节点的右子树还是左子树，将对应的指针赋值NULL
3、free待删除节点
实现代码：
/* 删除节点 */
/* cur为待删除节点， parent为待删除节点的父节点 */
void DeletNode(BSTree *parent, BSTree *cur, int DelData)
{
BSTree *SNode = NULL; //后继节点
BSTree *PSNode = NULL; //后继节点的父节点 if (cur == NULL)
{
printf("删除节点不存在\n");
exit();
}
else if (DelData > cur->data)
{
DeletNode(cur, cur->right, DelData);
}
else if (DelData < cur->data)
{
DeletNode(cur, cur->left, DelData);
}
else if(DelData == cur->data)
{
if (cur->left == NULL && cur->right == NULL) //待删除节点为叶子节点
{
if (parent->left == cur) //如果该节点是父节点的左子树
{
parent->left = NULL;
}
else if (parent->right == cur) //如果该节点是父节点的右子树
{
parent->right = NULL;
}
}
因为删除节点这个子函数我是用的不带返回值的递归实现的，导致if else语句很多，后面我把删除节点这个子函数改成带返回值的递归，看起来要舒服不少，代码如下，有兴趣的读者可以看一下
/* 删除节点 */
/* cur为待删除节点， parent为待删除节点的父节点 */
BSTree *DeletNode(BSTree *parent, BSTree *cur, int DelData)
{
BSTree *SNode = NULL; //后继节点
BSTree *PSNode = NULL; //后继节点的父节点
BSTree *temp = NULL; //临时保存待释放节点的子树，避免free后找不到左右子树 if (cur == NULL)
{
printf("删除节点不存在\n");
exit();
}
else if (DelData > cur->data)
{
cur->right = DeletNode(cur, cur->right, DelData);
}
else if (DelData < cur->data)
{
cur->left = DeletNode(cur, cur->left, DelData);
}
else if (DelData == cur->data)
{
if (cur->left == NULL && cur->right == NULL) //待删除节点为叶子节点
{
free(cur);
return NULL;
}
带返回值的递归实现
情形二：删除带有一个子节点的节点
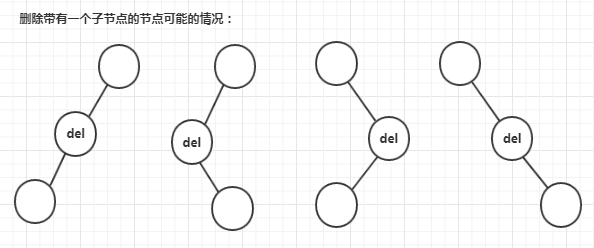
（图片来源：https://www.cnblogs.com/songwenjie/p/8973217.html）
上图写了四种，但对待删除节点来说只有两种，只有左子树，或只有右子树，两种情况的处理方式基本相同，都是将待删除节点的左/右子树 赋值给 待删除节点的父节点的左/右子树
实现代码：
else if(cur->left != NULL && cur->right == NULL) //待删除节点只有左子树
{
if (parent->left == cur)
{
parent->left = cur->left;
}
else if (parent->right == cur)
{
parent->right = cur->left;
}
free(cur); //释放待删除节点
}
else if(cur->left == NULL && cur->right != NULL) //待删除节点只有右子树
{
if (parent->left == cur)
{
parent->left = cur->right;
}
else if (parent->right == cur)
{
parent->right = cur->right;
}
free(cur); //释放待删除节点
}
else if(cur->left != NULL && cur->right == NULL) //待删除节点只有左子树
{
temp = cur->left;
free(cur); return temp;;
}
else if(cur->left == NULL && cur->right != NULL) //待删除节点只有右子树
{
temp = cur->right;
free(cur); return cur->right;
}
带返回值的递归实现
情形三：删除带两个节点的节点
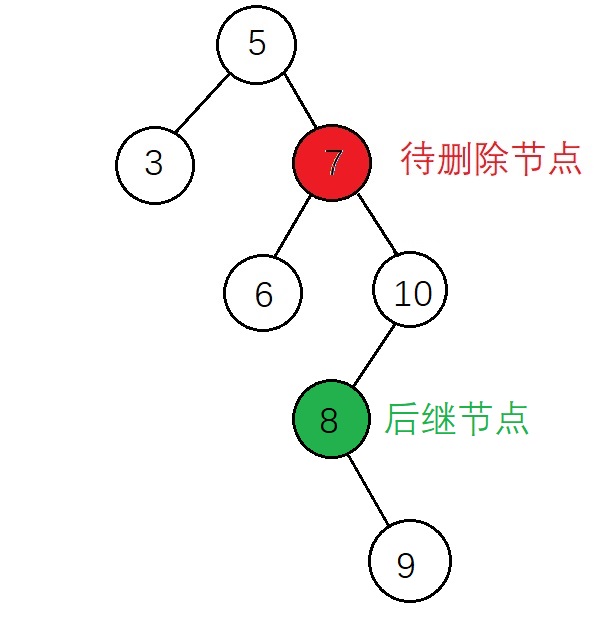
因为删除节点会有破坏 BST 正确结构的风险，删除带两个节点的节点操作显得较为复杂，首先需要找到待删除节点的 后继节点 和 该后继节点的父节点，（一个节点的后继节点是指，这个节点在中序遍历序列中的下一个节点，相应的，前驱节点是指这个节点在中序遍历序列中的上一个节点），删除节点的后继节点一定是删除节点右子树的最左侧节点，这篇随笔采用的方式是后继节点替代待删除节点的方式而不是前驱节点替代删除节点，需要考虑的情况如下
1、后继节点为待删除节点的子节点
在后继节点为待删除节点的子节点的前提下，该后继节点有右子树和没有右子树的操作是相同的，都是将 后继节点 替代 待删除节点，并将待删除节点的左子树 赋值给 后继节点的左子树
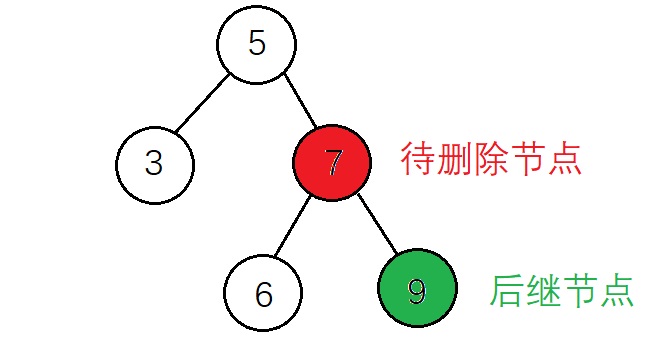
实现代码：
else if(cur->left != NULL && cur->right != NULL) //待删除节点既有左子树也有右子树
{
SNode = SearchSuccessorNode(cur->right); //搜索后继节点
PSNode = SearchParentofSNode(cur->right, cur->right); //搜索后继节点的父节点 if (cur->right == SNode) //后继节点为待删除节点的右子树（后继节点有右子树和没有右子树的操作相同）
{
if (parent->left == cur)
{
parent->left = SNode;
SNode->left = cur->left; free(cur);
}
else if (parent->right == cur)
{
parent->right = SNode;
SNode->left = cur->left; free(cur);
}
}
else if(cur->left != NULL && cur->right != NULL) //待删除节点既有左子树也有右子树
{
SNode = SearchSuccessorNode(cur->right); //搜索后继节点
PSNode = SearchParentofSNode(cur->right, cur->right); //搜索后继节点的父节点 if (cur->right == SNode) //后继节点为待删除节点的右子树（后继节点有右子树和没有右子树的操作相同）
{
SNode->left = cur->left;
free(cur); return SNode;
}
带返回值的递归实现
2、后继节点不为待删除节点的子节点
这里后继节点还要在分为后继节点有子节点和没有子节点的情况
（1）后继节点没有右子节点
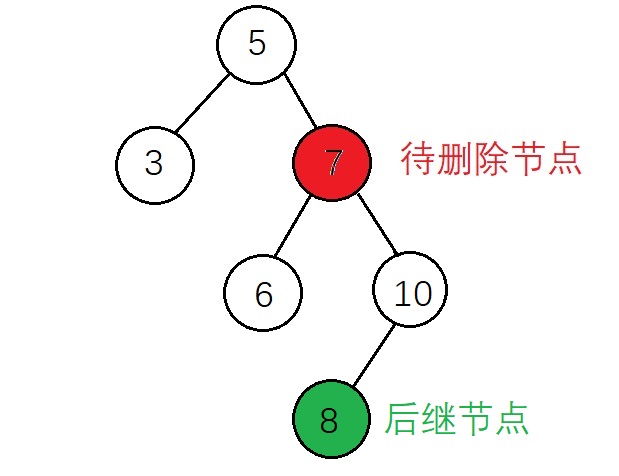
根据实现代码来标注上面的节点
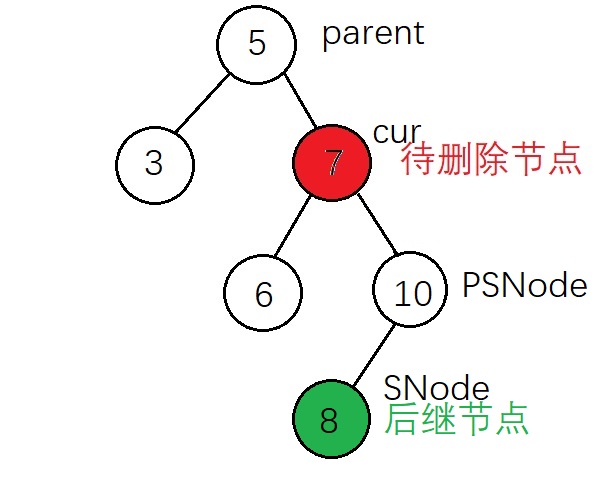
删除后：
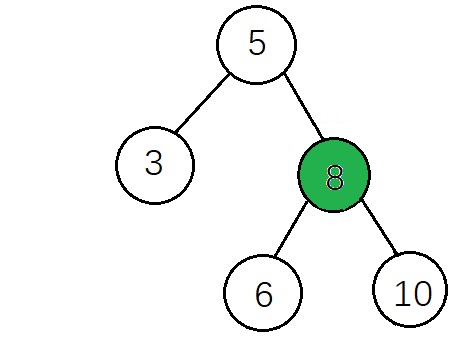
实现代码：
else if (cur->right != SNode && SNode->right == NULL) //后继节点不为待删除节点的右子树，并且该后继节点没有右子树
{
if (parent->left == cur)
{
parent->left = SNode;
SNode->left = cur->left;
SNode->right = cur->right;
PSNode->left = NULL; free(cur);
}
else if (parent->right == cur)
{
parent->right = SNode;
SNode->left = cur->left;
SNode->right = cur->right;
PSNode->left = NULL; free(cur);
}
}
else if (cur->right != SNode && SNode->right == NULL) //后继节点不为待删除节点的右子树，并且该后继节点没有右子树
{
SNode->left = cur->left;
SNode->right = cur->right;
PSNode->left = NULL;
free(cur); return SNode;
}
带返回值的递归实现
（2）后继节点有右子节点
删除后：
与上面的后继节点没有右子节点相比需要增加一个操作，需要将后继节点的右子树 赋值给 后继节点的父节点的左子树
实现代码：
else if (cur->right != SNode && SNode->right != NULL) //后继节点不为待删除节点的右子树，并且该后继节点有右子树
{
if (parent->left == cur)
{
parent->left = SNode;
PSNode->left = SNode->right; //后继节点的右子树作为后继节点父节点的左子树
SNode->left = cur->left;
SNode->right = cur->right; free(cur);
}
else if (parent->right == cur)
{
parent->right = SNode;
PSNode->left = SNode->right; //后继节点的右子树作为后继节点父节点的左子树
SNode->left = cur->left;
SNode->right = cur->right; free(cur);
}
}
else if (cur->right != SNode && SNode->right != NULL) //后继节点不为待删除节点的右子树，并且该后继节点有右子树
{ PSNode->left = SNode->right; //后继节点的右子树作为后继节点父节点的左子树
SNode->left = cur->left;
SNode->right = cur->right;
free(cur); return SNode;
}
带返回值的递归实现
测试数据：
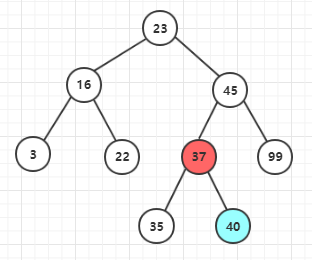
一、“后继节点是删除节点的子节点”（因为后继节点有无子树的操作相同，这里只测试没有子树的情况）
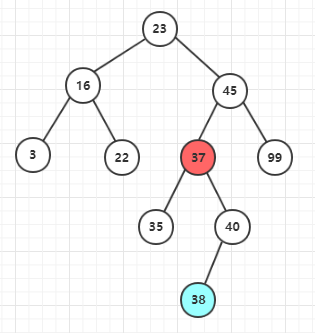
二、“后继节点不是删除节点的子节点，且后继节点没有右子树”
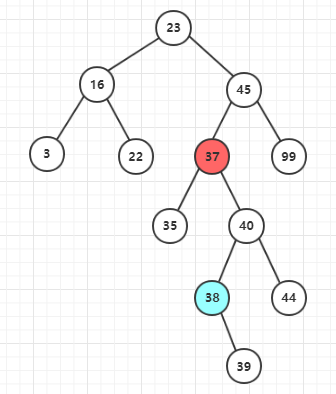
三、“后继节点不是删除节点的子节点，且后继节点有右子树”
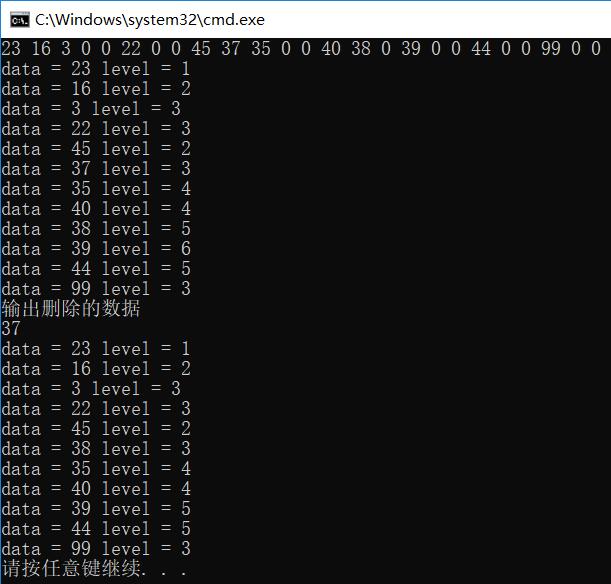
完整代码：（注：对free(cur)的位置进行了调整）
#include <stdio.h>
#include <stdlib.h>
#include <conio.h> #define LEFT 1
#define RIGHT 2 typedef struct BSTreeNode
{
int data;
struct BSTreeNode *left;//左子树
struct BSTreeNode *right;//右子树
}BSTree; BSTree *Create_BSTreeNode(BSTree *nod); //创建二叉查找树
void PreOrder_Traverse(BSTree *nod, int level); //前序遍历二叉树，并打印
void SearchData(int targ, BSTree *nod); //查找特定值
BSTree *AddNewNode(BSTree *cur, int NewData); //添加新的节点
void DeletNode(BSTree *parent, BSTree *cur, int DelData); //删除节点
BSTree *SearchSuccessorNode(BSTree *nod); //搜索后继节点
BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod); //搜索后继节点的父节点 int main()
{
BSTree *nod = NULL;
//int num;
int key;
//int del; nod = Create_BSTreeNode(nod);
PreOrder_Traverse(nod, ); //printf("输出查找数据\n");
//scanf_s("%d", &num, 1);
//SearchData(num, nod); printf("输出新插入数据\n");
scanf_s("%d", &key, );
nod = AddNewNode(nod, key); //printf("输出删除的数据\n");
//scanf_s("%d", &del, 1);
//DeletNode(nod, nod, del); PreOrder_Traverse(nod, ); return ;
} /* 搜索后继节点的父节点 */
BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod)
{
while ()
{
if (nod->left != NULL)
{
Pnod = nod;
nod = nod->left;
}
else
{
break;
}
} return Pnod;
} /* 搜索后继节点 */
BSTree *SearchSuccessorNode(BSTree *nod)
{
while ()
{
if (nod->left != NULL)
{
nod = nod->left;
}
else
{
break;
}
} return nod;
} /* 删除节点 */
/* cur为待删除节点， parent为待删除节点的父节点 */
void DeletNode(BSTree *parent, BSTree *cur, int DelData)
{
BSTree *SNode = NULL; //后继节点
BSTree *PSNode = NULL; //后继节点的父节点 if (DelData > cur->data)
{
DeletNode(cur, cur->right, DelData);
}
else if (DelData < cur->data)
{
DeletNode(cur, cur->left, DelData);
}
else if(DelData == cur->data)
{
if (cur->left == NULL && cur->right == NULL) //待删除节点为叶子节点
{
if (parent->left == cur) //如果该节点是父节点的左子树
{
parent->left = NULL;
}
else if (parent->right == cur) //如果该节点是父节点的右子树
{
parent->right = NULL;
}
}
else if(cur->left != NULL && cur->right == NULL) //待删除节点只有左子树
{
if (parent->left == cur)
{
parent->left = cur->left;
}
else if (parent->right == cur)
{
parent->right = cur->left;
}
}
else if(cur->left == NULL && cur->right != NULL) //待删除节点只有右子树
{
if (parent->left == cur)
{
parent->left = cur->right;
}
else if (parent->right == cur)
{
parent->right = cur->right;
}
}
else if(cur->left != NULL && cur->right != NULL) //待删除节点既有左子树也有右子树
{
SNode = SearchSuccessorNode(cur->right); //搜索后继节点
PSNode = SearchParentofSNode(cur->right, cur->right); //搜索后继节点的父节点 if (cur->right == SNode) //后继节点为待删除节点的右子树（后继节点有右子树和没有右子树的操作相同）
{
if (parent->left == cur)
{
parent->left = SNode;
SNode->left = cur->left;
}
else if (parent->right == cur)
{
parent->right = SNode;
SNode->left = cur->left;
}
}
else if (cur->right != SNode && SNode->right == NULL) //后继节点不为待删除节点的右子树，并且该后继节点没有右子树
{
if (parent->left == cur)
{
parent->left = SNode;
SNode->left = cur->left;
SNode->right = cur->right;
PSNode->left = NULL;
}
else if (parent->right == cur)
{
parent->right = SNode;
SNode->left = cur->left;
SNode->right = cur->right;
PSNode->left = NULL;
}
}
else if (cur->right != SNode && SNode->right != NULL) //后继节点不为待删除节点的右子树，并且该后继节点有右子树
{
if (parent->left == cur)
{
parent->left = SNode;
PSNode->left = SNode->right; //后继节点的右子树作为后继节点父节点的左子树
SNode->left = cur->left;
SNode->right = cur->right;
}
else if (parent->right == cur)
{
parent->right = SNode;
PSNode->left = SNode->right; //后继节点的右子树作为后继节点父节点的左子树
SNode->left = cur->left;
SNode->right = cur->right;
}
}
}
free(cur); //释放待删除节点
}
} /* 添加新节点 */
BSTree *AddNewNode(BSTree *cur, int NewData)
{
if (cur == NULL)
{
if ((cur = (BSTree *)malloc(sizeof(BSTree))) == NULL) //创建新节点
{
printf("内存不足");
exit();
}
cur->data = NewData;
cur->left = NULL;
cur->right = NULL; return cur;
}
if (NewData > cur->data)
{
cur->right = AddNewNode(cur->right, NewData);
}
else if (NewData < cur->data)
{
cur->left = AddNewNode(cur->left, NewData);
}
else if (NewData == cur->data)
{
printf("不允许插入重复值\n");
exit();
} return cur;
} /* 查找特定值 */
void SearchData(int targ, BSTree *nod)
{
if (nod != NULL)
{
if (nod->data == targ)
{
printf("查找值存在，值为%d\n", nod->data);
}
else if (nod->data > targ)
{
SearchData(targ, nod->left); //递归查找左子树
}
else if (nod->data < targ)
{
SearchData(targ, nod->right); //递归查找右子树
}
}
else if (nod == NULL)
{
printf("查找值不存在\n");
}
} /* 创建二叉查找树（数据以前序遍历顺序输入）*/
BSTree *Create_BSTreeNode(BSTree *nod)
{
int num; scanf_s("%d", &num, );
if (num == ) /* 假定输入的数据都为正数，以0作为NULL的标志 */
{
return NULL;
}
else
{
if ((nod = (BSTree *)malloc(sizeof(BSTree))) == NULL)
{
printf("内存空间不足");
exit();
}
nod->data = num;
nod->left = Create_BSTreeNode(nod->left);
nod->right = Create_BSTreeNode(nod->right); return nod;
}
} /* 前序遍历二叉树，并打印 */
void PreOrder_Traverse(BSTree *nod, int level)
{
if (nod == NULL)
{
return ;
} printf("data = %d level = %d\n", nod->data, level);
PreOrder_Traverse(nod->left, level + );
PreOrder_Traverse(nod->right, level + );
}
因为主要是分析二叉查找树的查找、插入、删除操作，没有考虑二叉树为空 或 待删除节点为根节点的情况
补充：（注：删除节点函数修改成了带返回值的递归实现——更新日期2019/8/13）
#include <stdio.h>
#include <stdlib.h>
#include <conio.h> #define LEFT 1
#define RIGHT 2 typedef struct BSTreeNode
{
int data;
struct BSTreeNode *left;//左子树
struct BSTreeNode *right;//右子树
}BSTree; BSTree *Create_BSTreeNode(BSTree *nod); //创建二叉查找树
void PreOrder_Traverse(BSTree *nod, int level); //前序遍历二叉树，并打印
void SearchData(int targ, BSTree *nod); //查找特定值
BSTree *AddNewNode(BSTree *cur, int NewData); //添加新的节点
BSTree *DeletNode(BSTree *parent, BSTree *cur, int DelData); //删除节点
BSTree *SearchSuccessorNode(BSTree *nod); //搜索后继节点
BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod); //搜索后继节点的父节点 int main()
{
BSTree *nod = NULL;
//int num;
//int key;
int del; nod = Create_BSTreeNode(nod);
PreOrder_Traverse(nod, ); /*printf("输出查找数据\n");
scanf_s("%d", &num, 1);
SearchData(num, nod);*/ /*printf("输出新插入数据\n");
scanf_s("%d", &key, 1);
nod = AddNewNode(nod, key);*/ printf("输出删除的数据\n");
scanf_s("%d", &del, );
nod = DeletNode(nod, nod, del); PreOrder_Traverse(nod, ); return ;
} /* 搜索后继节点的父节点 */
BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod)
{
while ()
{
if (nod->left != NULL)
{
Pnod = nod;
nod = nod->left;
}
else
{
break;
}
} return Pnod;
} /* 搜索后继节点 */
BSTree *SearchSuccessorNode(BSTree *nod)
{
while ()
{
if (nod->left != NULL)
{
nod = nod->left;
}
else
{
break;
}
} return nod;
} /* 删除节点 */
/* cur为待删除节点， parent为待删除节点的父节点 */
BSTree *DeletNode(BSTree *parent, BSTree *cur, int DelData)
{
BSTree *SNode = NULL; //后继节点
BSTree *PSNode = NULL; //后继节点的父节点
BSTree *temp = NULL; //临时保存待释放节点的子树，避免free后找不到左右子树 if (cur == NULL)
{
printf("删除节点不存在\n");
exit();
}
else if (DelData > cur->data)
{
cur->right = DeletNode(cur, cur->right, DelData);
}
else if (DelData < cur->data)
{
cur->left = DeletNode(cur, cur->left, DelData);
}
else if (DelData == cur->data)
{
if (cur->left == NULL && cur->right == NULL) //待删除节点为叶子节点
{
free(cur);
return NULL;
}
else if(cur->left != NULL && cur->right == NULL) //待删除节点只有左子树
{
temp = cur->left;
free(cur); return temp;;
}
else if(cur->left == NULL && cur->right != NULL) //待删除节点只有右子树
{
temp = cur->right;
free(cur); return cur->right;
}
else if(cur->left != NULL && cur->right != NULL) //待删除节点既有左子树也有右子树
{
SNode = SearchSuccessorNode(cur->right); //搜索后继节点
PSNode = SearchParentofSNode(cur->right, cur->right); //搜索后继节点的父节点 if (cur->right == SNode) //后继节点为待删除节点的右子树（后继节点有右子树和没有右子树的操作相同）
{
SNode->left = cur->left;
free(cur); return SNode;
}
else if (cur->right != SNode && SNode->right == NULL) //后继节点不为待删除节点的右子树，并且该后继节点没有右子树
{
SNode->left = cur->left;
SNode->right = cur->right;
PSNode->left = NULL;
free(cur); return SNode;
}
else if (cur->right != SNode && SNode->right != NULL) //后继节点不为待删除节点的右子树，并且该后继节点有右子树
{ PSNode->left = SNode->right; //后继节点的右子树作为后继节点父节点的左子树
SNode->left = cur->left;
SNode->right = cur->right;
free(cur); return SNode;
}
}
} return cur;
} /* 添加新节点 */
BSTree *AddNewNode(BSTree *cur, int NewData)
{
if (cur == NULL)
{
if ((cur = (BSTree *)malloc(sizeof(BSTree))) == NULL) //创建新节点
{
printf("内存不足");
exit();
}
cur->data = NewData;
cur->left = NULL;
cur->right = NULL; return cur;
}
if (NewData > cur->data)
{
cur->right = AddNewNode(cur->right, NewData);
}
else if (NewData < cur->data)
{
cur->left = AddNewNode(cur->left, NewData);
}
else if (NewData == cur->data)
{
printf("不允许插入重复值\n");
exit();
} return cur;
} /* 查找特定值 */
void SearchData(int targ, BSTree *nod)
{
if (nod != NULL)
{
if (nod->data == targ)
{
printf("查找值存在，值为%d\n", nod->data);
}
else if (nod->data > targ)
{
SearchData(targ, nod->left); //递归查找左子树
}
else if (nod->data < targ)
{
SearchData(targ, nod->right); //递归查找右子树
}
}
else if (nod == NULL)
{
printf("查找值不存在\n");
}
} /* 创建二叉查找树（数据以前序遍历顺序输入）*/
BSTree *Create_BSTreeNode(BSTree *nod)
{
int num; scanf_s("%d", &num, );
if (num == ) /* 假定输入的数据都为正数，以0作为NULL的标志 */
{
return NULL;
}
else
{
if ((nod = (BSTree *)malloc(sizeof(BSTree))) == NULL)
{
printf("内存空间不足");
exit();
}
nod->data = num;
nod->left = Create_BSTreeNode(nod->left);
nod->right = Create_BSTreeNode(nod->right); return nod;
}
} /* 前序遍历二叉树，并打印 */
void PreOrder_Traverse(BSTree *nod, int level)
{
if (nod == NULL)
{
return ;
} printf("data = %d level = %d\n", nod->data, level);
PreOrder_Traverse(nod->left, level + );
PreOrder_Traverse(nod->right, level + );
}
二叉查找树（查找、插入、删除）——C语言的更多相关文章
- 数据结构与算法->树->2-3-4树的查找,添加,删除(Java)
代码: 兵马未动,粮草先行 作者: 传说中的汽水枪 如有错误,请留言指正,欢迎一起探讨. 转载请注明出处. 目录 一. 2-3-4树的定义 二. 2-3-4树数据结构定义 三. 2-3-4树的可以得到 ...
- 数据结构系列之2-3-4树的插入、查找、删除和遍历完整版源代码实现与分析（dart语言实现）
本文属于原创,转载请注明来源. 在上一篇博文中,详细介绍了2-3树的操作(具体地址:https://www.cnblogs.com/outerspace/p/10861488.html),那么对于更多 ...
- Java实现二叉排序树的插入、查找、删除
import java.util.Random; /** * 二叉排序树(又称二叉查找树) * (1)能够是一颗空树 * (2)若左子树不空,则左子树上全部的结点的值均小于她的根节点的值 * (3)若 ...
- 【数据结构】——搜索二叉树的插入，查找和删除（递归&非递归）
一.搜索二叉树的插入,查找,删除 简单说说搜索二叉树概念: 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右 ...
- DS-二叉排序树的插入、查找和删除
2019-12-02(菜鸡开始学习了...) Data Structure 之 二叉排序树 二叉排序树是给定一个节点后,接下来插入的数如果比它大就会放到它的右孩子那边,比它小就会放到它的左孩子那边. ...
- Splay的基本操作(插入/删除,查询)
Splay的基本操作(插入/删除,查询) 概述 这是一棵二叉查找树 让频繁访问的节点尽量靠近根 将查询,插入等操作的点"旋转"至根 树的高度均摊为$log_n$ 变量 int ro ...
- leveldb源码分析--插入删除流程
由于网络上对leveldb的分析文章都比较丰富,一些基础概念和模型都介绍得比较多,所以本人就不再对这些概念以专门的篇幅进行介绍,本文主要以代码流程注释的方式. 首先我们从db的插入和删除开始以对整个体 ...
- 洛谷 P2042 [NOI2005]维护数列-Splay(插入 删除 修改 翻转 求和 最大的子序列)
因为要讲座,随便写一下,等讲完有时间好好写一篇splay的博客. 先直接上题目然后贴代码,具体讲解都写代码里了. 参考的博客等的链接都贴代码里了,有空再好好写. P2042 [NOI2005]维护数列 ...
- jQery实现插入删除信息
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/ ...
- [LeetCode] Insert Delete GetRandom O(1) - Duplicates allowed 常数时间内插入删除和获得随机数 - 允许重复
Design a data structure that supports all following operations in average O(1) time. Note: Duplicate ...
随机推荐
- redis整合springboot的helloworld
引入依赖 compile 'org.springframework.boot:spring-boot-starter-data-redis' 使用redis有两种方法 1.Jedis Jedis je ...
- Codeforces Gym101246H：``North-East''（LIS+思维）
http://codeforces.com/gym/101246/problem/H 题意:在二维平面上有n个点,从最左下角的点出发,每次走只能走在当前的点的右上角的点(xj > xi, yj ...
- POJ 1986：Distance Queries（倍增求LCA）
http://poj.org/problem?id=1986 题意:给出一棵n个点m条边的树,还有q个询问,求树上两点的距离. 思路:这次学了一下倍增算法求LCA.模板. dp[i][j]代表第i个点 ...
- Java 中的字符串(String)与C# 中字符串(string)的异同
1. C# 中比较两个字符串字面量是否相等,可以使用 “==”比较运算符,是因为string 类型重写(override)了“==” 和 “!=” 运算符,在使用“==” 和 “!=” 进行字符串比较 ...
- C#8.0: 在 LINQ 中支持异步的 IAsyncEnumerable
C# 8.0中,提供了一种新的IAsyncEnumerable<T>接口,在对集合进行迭代时,支持异步操作.比如在读取文本中的多行字符串时,如果读取每行字符串的时候使用同步方法,那么会导致 ...
- java网络爬虫，乱码问题终于完美解决
第一次写爬虫,被乱码问题困扰两天,试了很多方法都不可以,今天随便一试,居然好了. 在获取网页时创建了一个缓冲字节输入流,问题就在这个流上,添加标红代码即可 BufferedReader in = nu ...
- Spring Boot 邮件发送的 5 种姿势！
邮件发送其实是一个非常常见的需求,用户注册,找回密码等地方,都会用到,使用 JavaSE 代码发送邮件,步骤还是挺繁琐的,Spring Boot 中对于邮件发送,提供了相关的自动化配置类,使得邮件发送 ...
- Fiolki题解
问题 B: Fiolki 时间限制: 3 Sec 内存限制: 128 MB 题目描述 化学家吉丽想要配置一种神奇的药水来拯救世界. 吉丽有n种不同的液体物质,和n个药瓶(均从1到n编号).初始时,第 ...
- 1.低权限的程序向高权限的程序发消息 2.慎用setcurrentdirectory
1.低权限的程序向高权限的程序发消息 2.慎用setcurrentdirectory
- Spring 自动生成getter和setter方法 tostring方法
添加maven依赖 <!-- https://mvnrepository.com/artifact/org.projectlombok/lombok --> <dependency& ...