Codeforces Round #324 (Div. 2) D. Dima and Lisa 哥德巴赫猜想

D. Dima and Lisa

Time Limit: 1 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/584/problem/D

Description

Dima loves representing an odd number as the sum of multiple primes, and Lisa loves it when there are at most three primes. Help them to represent the given number as the sum of at most than three primes.

More formally, you are given an odd numer n. Find a set of numbers p_i (1 ≤ i ≤ k), such that

1. 1 ≤ k ≤ 3
2. p_i is a prime
3. 

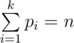
The numbers p_i do not necessarily have to be distinct. It is guaranteed that at least one possible solution exists.

Input

The single line contains an odd number n (3 ≤ n < 10⁹).

Output

In the first line print k (1 ≤ k ≤ 3), showing how many numbers are in the representation you found.

In the second line print numbers p_i in any order. If there are multiple possible solutions, you can print any of them.

Sample Input

27

Sample Output

3

5 11 11

HINT

题意

给你一个奇数n，然后让你找到k（k<=3)个质数，使得这k个质数加起来等于n

题解：

哥德巴赫猜想，任何一个大于2的偶数都可以由俩素数组成

于是我们就让n-3，然后暴力搞就行了……

素数其实是非常密集的，在n->2n之间 一定有一个素数

所以这个复杂度还是比较客观的（雾

代码：

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <bitset>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 110
#define eps 1e-9
int Num;
//const int inf=0x7fffffff;   //§&szlig;§é§à§é¨f§3
const int inf=0x3f3f3f3f;
inline ll read()
{
    ll x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
//**************************************************************************************

//****************************************************************
// Miller_Rabin 算法进行素数测试
//速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=;//随机算法判定次数，S越大，判错概率越小

//计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
//  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=;
    while(b)
    {
        if(b&){ret+=a;ret%=c;}
        a<<=;
        if(a>=c)a%=c;
        b>>=;
    }
    return ret;
}

//计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=;
    while(n)
    {
        if(n&) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=;
    }
    return ret;
}

//以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==&&last!=&&last!=n-) return true;//合数
        last=ret;
    }
    if(ret!=) return true;
    return false;
}

// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数，但概率极小)
//合数返回false;

bool Miller_Rabin(long long n)
{
    if(n<)return false;
    if(n==)return true;
    if((n&)==) return false;//偶数
    long long x=n-;
    long long t=;
    while((x&)==){x>>=;t++;}
    for(int i=;i<S;i++)
    {
        long long a=rand()%(n-)+;//rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}

//************************************************
//pollard_rho 算法进行质因数分解
//************************************************

long long gcd(long long a,long long b)
{
    if(a==)return ;//??????
    if(a<) return gcd(-a,b);
    while(b)
    {
        long long t=a%b;
        a=b;
        b=t;
    }
    return a;
}
//&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
const int MAXN = ;
bool flag[MAXN];
int primes[MAXN], pi;
void GetPrime_1()
{
    int i, j;
    pi = ;
    memset(flag, false, sizeof(flag));
    for (i = ; i < MAXN; i++)
        if (!flag[i])
        {
            primes[i] = ;//素数标识为1
            for (j = i; j < MAXN; j += i)
                flag[j] = true;
        }
}

ll p[maxn];
vector<int> DDD;
int main()
{
    srand(time(NULL));
    GetPrime_1();
    int tot = ;
    for(int i=;;i++)
    {
        if(tot>)break;
        if(primes[i])
        {
            DDD.push_back(i);
            tot++;
        }
    }
    ll n;cin>>n;
    if(Miller_Rabin(n))
    {
        cout<<""<<endl;
        cout<<n<<endl;
        return ;
    }
    if(Miller_Rabin(n-))
    {
        cout<<""<<endl;
        cout<<"2 "<<n-<<endl;
        return ;
    }
    if(n<)
    {
        for(int i=;i<DDD.size();i++)
        {
            for(int j=i;j<=DDD.size();j++)
            {
                if(DDD[j]+DDD[i]>n)break;
                if(Miller_Rabin(n-DDD[i]-DDD[j]))
                {
                    printf("3\n");
                    printf("%d %d %d\n",DDD[i],DDD[j],n-DDD[i]-DDD[j]);
                    return ;
                }
            }
        }
    }
    else
    {
        n-=;
        for(int i=n-;i>=;i--)
        {
            int x = n-i,y = i;
            if(Miller_Rabin(x)&&Miller_Rabin(y))
            {
                printf("3\n");
                cout<<"3 "<<x<<" "<<y<<endl;
                return ;
            }
        }
    }
}