POJ-3131-Cubic Eight-Puzzle(双向BFS+哈希)

Description

Let’s play a puzzle using eight cubes placed on a 3 × 3 board leaving one empty square.

Faces of cubes are painted with three colors. As a puzzle step, you can roll one of the cubes to a adjacent empty square. Your goal is to make the specified color pattern visible from above by a number of such steps.

The rules of this puzzle are as follows.

1. Coloring of Cubes: All the cubes area colored in the same way as shown in Figure 1. The opposite faces have the same color.

   

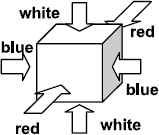
   Figure 1: Coloring of a cube

2. Initial Board State: Eight cubes are placed on the 3 × 3 board leaving one empty square. All the cubes have the same orientation as shown in Figure 2. As shown in the figure, squares on the board are given x and y coordinates,
   (1, 1), (1, 2), …, and (3, 3). The position of the initially empty square may vary.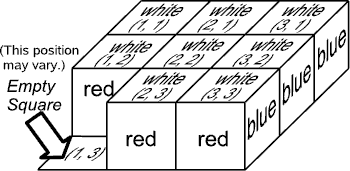

   

   Figure 2: Initial board state

3. Rolling Cubes: At each step, we can choose one of the cubes adjacent to the empty square and roll it into the empty square, leaving the original position empty. Figure 3 shows an example.

   

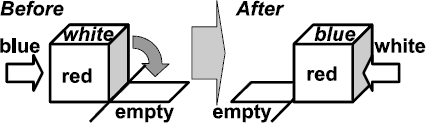
   Figure 3: Rolling a cube

4. Goal: The goal of this puzzle is to arrange the cubes so that their top faces form the specified color pattern by a number of cube rolling steps described above.

Your task is to write a program that finds the minimum number of steps required to make the specified color pattern from the given initial state.

Input

The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets is less than 16. Each dataset is formatted as follows.

x	y
F11	F21	F31
F12	F22	F32
F13	F23	F33

The first line contains two integers x and y separated by a space, indicating the position (x, y) of the initially empty square. The values of x and y are 1, 2, or 3.

The following three lines specify the color pattern to make. Each line contains three characters F_1j, F_2j, and F_3j, separated by a space. Character F_ij indicates
the top color of the cube, if any, at the position (i, j) as follows:

B: Blue,

W: White,

R: Red,

E: the square is Empty.

There is exactly one ‘E’ character in each dataset.

Output

For each dataset, output the minimum number of steps to achieve the goal, when the goal can be reached within 30 steps. Otherwise, output “-1” for the dataset.

Sample Input

1 2
W W W
E W W
W W W
2 1
R B W
R W W
E W W
3 3
W B W
B R E
R B R
3 3
B W R
B W R
B E R
2 1
B B B
B R B
B R E
1 1
R R R
W W W
R R E
2 1
R R R
B W B
R R E
3 2
R R R
W E W
R R R
0 0

Sample Output

0
3
13
23
29
30
-1
-1

Source

Japan 2006

思路：数据太大，先抽象出状态，再哈希一下，然后就是双向BFS。

#include <stdio.h>
#include <string.h>
#include <stack>
using namespace std;
#define INF 99999999

struct{
int step,state;
}t,que1[1000000],que2[1000000];

stack<int>stk;

bool vis1[5000007],vis2[5000007];
int top1,top2,bottom1,bottom2,mp[9],nxt[2][7]={{0,4,6,5,1,3,2},{0,5,3,2,6,1,4}},head[5000007],next[5000007],val[5000007],total;

int hashval(int x)
{
    int t,i;

    t=x%5000007;

    for(i=head[t];i!=-1;i=next[i])
    {
        if(val[i]==x) return i;
    }

    val[total]=x;
    next[total]=head[t];
    head[t]=total;
    total++;

    return total-1;
}

void pushtarget(int cnt,int state)
{
    if(cnt==-1)
    {
        vis2[hashval(state)]=1;
        que2[bottom2].step=0;
        que2[bottom2].state=state;
        bottom2++;

        return;
    }

    if(mp[cnt]%2)
    {
        pushtarget(cnt-1,state*7+mp[cnt]);
        pushtarget(cnt-1,state*7+mp[cnt]+1);
    }
    else pushtarget(cnt-1,state*7);
}

int getstate()
{
    int temp=0;

    for(int i=8;i>=0;i--)
    {
        temp=temp*7+mp[i];
    }

    return temp;
}

void spread(int x)
{
    int i=0,temp,cnt,old;

    while(i<9)
    {
        if(x%7==0) cnt=i;
        mp[i++]=x%7;
        x/=7;
    }

    cnt+=1;
    if(cnt>=0 && cnt<9 && cnt%3>0)
    {

        old=mp[cnt];
        mp[cnt-1]=nxt[0][mp[cnt]];
        mp[cnt]=0;

        stk.push(getstate());

        mp[cnt]=old;
        mp[cnt-1]=0;
    }
    cnt-=1;

    cnt-=1;
    if(cnt>=0 && cnt<9 && cnt%3<2)
    {
        old=mp[cnt];
        mp[cnt+1]=nxt[0][mp[cnt]];
        mp[cnt]=0;

        stk.push(getstate());

        mp[cnt]=old;
        mp[cnt+1]=0;
    }
    cnt+=1;

    cnt-=3;
    if(cnt>=0 && cnt<9)
    {
        old=mp[cnt];
        mp[cnt+3]=nxt[1][mp[cnt]];
        mp[cnt]=0;

        stk.push(getstate());

        mp[cnt]=old;
        mp[cnt+3]=0;
    }
    cnt+=3;

    cnt+=3;
    if(cnt>=0 && cnt<9)
    {
        old=mp[cnt];
        mp[cnt-3]=nxt[1][mp[cnt]];
        mp[cnt]=0;

        stk.push(getstate());

        mp[cnt]=old;
        mp[cnt-3]=0;
    }
    cnt-=3;
}

int bfs()
{
    int step1=0,step2=0,ans=INF,temp;

    for(step1=0;step1<=20;step1++)
    {

        while(top1<bottom1 && que1[top1].step==step1)
        {
            spread(que1[top1].state);

            while(!stk.empty())
            {
                temp=stk.top();
                stk.pop();

                if(vis2[hashval(temp)])
                {
                    return step1+step2+1;
                }

                if(!vis1[hashval(temp)])
                {
                    vis1[hashval(temp)]=1;
                    que1[bottom1].state=temp;
                    que1[bottom1].step=que1[top1].step+1;

                    bottom1++;
                }
            }

            top1++;
        }

        while(top2<bottom2 && que2[top2].step==step2 && step2<9)
        {
            spread(que2[top2].state);

            while(!stk.empty())
            {
                temp=stk.top();
                stk.pop();

                if(vis1[hashval(temp)]) return step1+step2+2;

                if(!vis2[hashval(temp)])
                {
                    vis2[hashval(temp)]=1;
                    que2[bottom2].state=temp;
                    que2[bottom2].step=step2+1;

                    bottom2++;
                }
            }

            top2++;
        }

        if(step2<9) step2++;
    }

    return -1;
}

int main()
{
    int x,y,i,j,temp;
    char ctemp;

    while(~scanf("%d%d",&y,&x) && x)
    {
        x--;
        y--;

        top1=top2=bottom1=bottom2=0;

        memset(vis1,0,sizeof vis1);
        memset(vis2,0,sizeof vis2);
        memset(head,-1,sizeof head);

        total=0;

        while(!stk.empty()) stk.pop();

        for(i=0;i<9;i++)
        {
            ctemp=getchar();

            if(ctemp=='\n' || ctemp==' ')
            {
                i--;
                continue;
            }

            if(ctemp=='W')mp[i]=1;
            else if(ctemp=='B') mp[i]=3;
            else if(ctemp=='R') mp[i]=5;
            else if(ctemp=='E') mp[i]=0;
        }

        pushtarget(8,0);

        temp=0;
        for(i=8;i>=0;i--)
        {
            if(i!=x*3+y) temp=temp*7+1;
            else temp*=7;
        }

        if(vis2[hashval(temp)])
        {
            printf("0\n");
            continue;
        }

        vis1[hashval(temp)]=1;

        que1[bottom1].step=0;
        que1[bottom1].state=temp;
        bottom1++;

        printf("%d\n",bfs());
    }
}