Deep Learning基础--Softmax求导过程

一、softmax函数

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是：

$$  S_i = \frac{e^j }{ \sum\nolimits_{j} e^j}  \tag{1}$$

更形象的如下图表示：

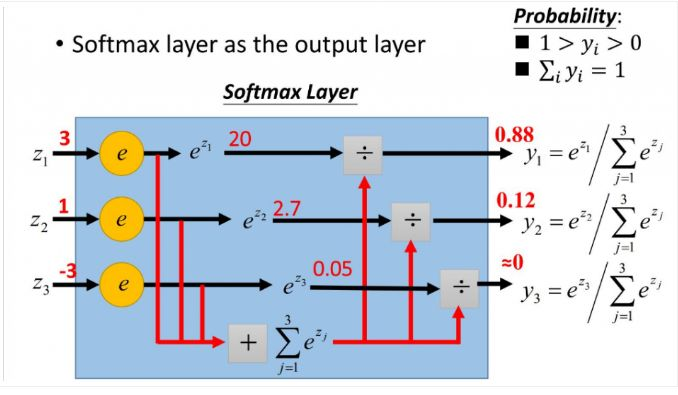
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标。

二、softmax相关求导

当我们对分类的Loss进行改进的时候，我们要通过梯度下降，每次优化一个step大小的梯度，这个时候我们就要求Loss对每个权重矩阵的偏导，然后应用链式法则。那么这个过程的第一步，就是对softmax求导传回去，不用着急，我后面会举例子非常详细的说明。在这个过程中，你会发现用了softmax函数之后，梯度求导过程非常非常方便。

下面我们举出一个简单例子。

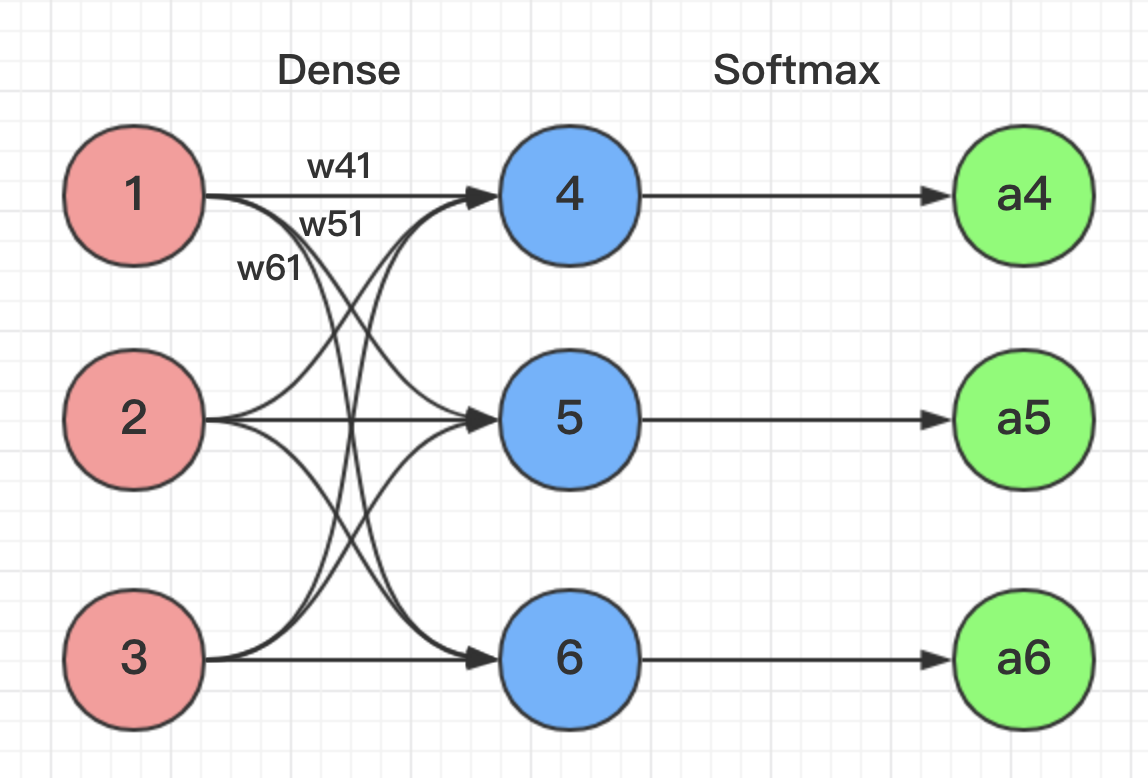
根据图片网络所示，我们能得到下面公式：

z4 = w41*o1+w42*o2+w43*o3

z5 = w51*o1+w52*o2+w53*o3

z6 = w61*o1+w62*o2+w63*o3

z4,z5,z6分别代表结点4,5,6的输出，01,02,03代表是结点1,2,3往后传的输入.

那么我们可以经过softmax函数得到：

$$a_4 = \frac{e^{z_4}}{e^{z_4} + e^{z_5} + e^{z_6}}, a_5 = \frac{e^{z_5}}{e^{z_4} + e^{z_5} + e^{z_6}}, a_6 = \frac{e^{z_6}}{e^{z_4} + e^{z_5} + e^{z_6}}   \tag{2}$$

经过上面的形式化后，接下来我们选用交叉熵作为损失函数来推导Softmax的偏导。交叉熵的形式为：

$$ Loss = -\sum_{i} y_i \cdot \ln a_i    \tag{3}$$

其中$y$代表我们的真实值，$a$代表我们softmax求出的值。$i$代表的是输出结点的标号。

为了形式化说明，我这里认为训练数据的真实输出为第$j$个为1，其它均为0，那么Loss就变成了$Loss = - y_j \cdot \ln a_j = - \ln a_j$，累和已经去掉，现在我们开始求导数。

参数的形式在该例子中，总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些，那么比如我要求出w41,w42,w43的偏导，就需要将Loss函数求偏导传到结点4，然后再利用链式法则继续求导即可。

举个例子此时求w41的偏导为:

$$
\frac{\partial Loss}{\partial w_{41}} = \frac{\partial Loss}{\partial a_{4}} \cdot \frac{\partial a_4}{\partial z_{4}} \cdot \frac{\partial z_4}{\partial w_{41}}
\\= - \frac{1}{a_4} \cdot \frac{\partial a_4}{\partial z_{4}} \cdot 1  \tag{4}
$$

上式中，只要求出$\frac{\partial a_4}{\partial z_{4}}$就可以完成推导。这里分为两种情况：

1. 当$j=i$时：

$$ \frac{\partial a_j}{\partial z_i} = \frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_k e^{z_k}})
\\=\frac{(e^{z_j})' \cdot \sum_k e^{z_k} - e^{z_j} \cdot e^{z_j}}{(\sum_k e^{z_k})^2}
\\=\frac{e^{z_j}}{\sum_k e^{z_k}} - \frac{e^{z_j}}{\sum_k e^{z_k}} \cdot \frac{e^{z_j}}{\sum_k e^{z_k}}
\\=a_j \cdot (1-a_j)
\tag{5} $$

将（5）式带入（4）中，得到$ \frac{\partial Loss}{\partial w_{j}} = -\frac{1}{a_j} \cdot a_j \cdot (1-a_j) = a_j - 1$。

2. 当$j \neq i$时：

$$ \frac{\partial a_j}{\partial z_i} = \frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_k e^{z_k}})
\\=\frac{0 \cdot \sum_k e^{z_k} - e^{z_j} \cdot e^{z_i}}{(\sum_k e^{z_k})^2}
\\=- \frac{e^{z_j}}{\sum_k e^{z_k}} \cdot \frac{e^{z_i}}{\sum_k e^{z_k}}
\\=-a_j \cdot a_i
\tag{6} $$

将（6）式带入（4）中，得到$ \frac{\partial Loss}{\partial w_{j}} = -\frac{1}{a_j} \cdot -a_j \cdot a_i = a_i$。

OK，到此我们已经完全推导完Softmax部分的反向传播。

参考：

1. https://zhuanlan.zhihu.com/p/25723112

2. https://blog.csdn.net/u014313009/article/details/51045303