MT【1】终点在球面上的向量

解答:
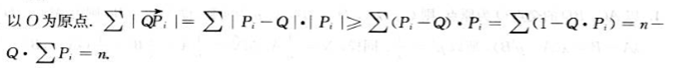
评:最小值在Q为球心时取到,体现数学对称性的美!
MT【1】终点在球面上的向量的更多相关文章
- python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)(向量的第二范数为传统意义上的向量长度),(如何求取向量的单位向量)
求取向量二范数,并求取单位向量(行向量计算) import numpy as np x=np.array([[0, 3, 4], [2, 6, 4]]) y=np.linalg.norm(x, axi ...
- UVA10827球面上的最大和
题意: 最大子矩阵的加强版,就是给你一个n*n的矩阵,每个格子里面都有数字,然后我们在里面选择一个矩阵,使得矩阵中所有数字的和最大,而且这个题目说这个n*n的矩阵的最右边和最左边是相邻的,最 ...
- 【转载】屏幕坐标向3维坐标的转化-DXUT的CD3DArcBall类
原文:http://blog.csdn.net/bluekitty/article/details/6070828 3D应用程序中,我们可以通过鼠标进行空间中物体的旋转和视角的变换等,而鼠标的移动是2 ...
- 3D数学读书笔记——向量运算及在c++上的实现
本系列文章由birdlove1987编写.转载请注明出处. 文章链接: http://blog.csdn.net/zhurui_idea/article/details/24782661 ...
- 线性代数的本质与几何意义 01. 向量是什么?(3blue1brown 咪博士 图文注解版)
向量是线性代数最基础.最基本的概念之一,要深入理解线性代数的本质,首先就要搞清楚向量到底是什么? 向量之所以让人迷糊,是因为我们在物理.数学,以及计算机等许多地方都见过它,但又没有彻底弄懂,以至于似是 ...
- OpenGL 用三角形模拟生成球面
在看OpenGL红皮书,看到生成球体这节,讲了很多,总感觉不如自己动手写一些代码来的实在,用OpenGL中三角形模拟球形生成.主要要点,模型视图变换,多边形表面环绕一致性,矩阵堆栈.先贴上代码. 虽然 ...
- 向量的表示及协方差矩阵 (PCA的理论基础)
原文:http://blog.csdn.net/songzitea/article/details/18219237 引言 当面对的数据被抽象为一组向量,那么有必要研究一些向量的数学性质.而这些数学性 ...
- [BZOJ4311]向量(凸包+三分+线段树分治)
可以发现答案一定在所有向量终点形成的上凸壳上,于是在上凸壳上三分即可. 对于删除操作,相当于每个向量有一个作用区间,线段树分治即可.$O(n\log^2 n)$ 同时可以发现,当询问按斜率排序后,每个 ...
- PCA算法详解——本质上就是投影后使得数据尽可能分散(方差最大),PCA可以被定义为数据在低维线性空间上的正交投影,这个线性空间被称为主⼦空间(principal subspace),使得投影数据的⽅差被最⼤化(Hotelling, 1933),即最大方差理论。
PCA PCA(Principal Component Analysis,主成分分析)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量 ...
随机推荐
- CF1097D Makoto and a Blackboard 积性函数、概率期望、DP
传送门 比赛秒写完ABC结果不会D--最后C还fst了qwq 首先可以想到一个约数个数\(^2\)乘上\(K\)的暴力DP,但是显然会被卡 在\(10^{15}\)范围内因数最多的数是\(978217 ...
- LInq之Take Skip TakeWhile SkipWhile Reverse Union Concat 用法
废话不多说,直接上代码,代码有注释!自行运行测试! class Program { static void Main(string[] args) { string[] names = { " ...
- python 常见矩阵运算
python 的 numpy 库提供矩阵运算的功能,因此我们在需要矩阵运算的时候,需要导入 numpy 的包. 1.numpy 的导入和使用 from numpy import *;#导入numpy的 ...
- centos7 清除系统日志、历史记录(包括history)、登录信息
history: # echo > .bash_history //清除保存的用户操作历史记录 # history -cw //清除所有历史 centos7 清除系统日志.历史记录.登录信息: ...
- VS2010、VS2012、VS2013、VS2015、VS2017各版本产品激活秘钥
Visual Studio 2017(VS2017) 企业版 Enterprise 注册码:NJVYC-BMHX2-G77MM-4XJMR-6Q8QF Visual Studio 2017(VS201 ...
- OpenDaylight(Oxygen)安装feature出现错误的解决方案
在使用OpenDaylight控制器时,初次进入karaf命令行下都需要先进行feature的安装 在使用Nitrogen版本(0.7.x)时,组件的安装可以类似 feature:install od ...
- 分布式监控系统Zabbix-添加windows监控主机
大多数情况下,线上服务器都是linux系统,但是偶尔也会有些windows机器.下面简单介绍下zabbix添加windows监控机的操作:1)下载windows的zabbix_agent下载地址:ht ...
- Python_函数_复习_习题_24
# 函数 # 可读性强 复用性强# def 函数名(): # 函数体 #return 返回值# 所有的函数 只定义不调用就一定不执行 #先定义后调用 #函数名() #不接收返回值#返回值 = 函数名( ...
- 【M2】软件工程终期总结报告——阅读作业
PhylabWeb——阅读作业 问题回顾 提问博客地址:http://www.cnblogs.com/kibbon/p/4831104.html 尚待解决的问题: Alpha/Beta,ZBB/RC阶 ...
- 在Java中执行Tomcat中startup.bat
问题:更改数据库时,需要重启Tomcat服务器,才能把更改后的数据加载到项目中.于是想每次更改数据库时,都调用Java方法,重启Tomcat 代码: Process process = Runtime ...
