N皇后问题（DFS）

题目：在N*N的国际象棋棋盘上放置N个皇后彼此不受攻击（即在棋盘的任一行，任一列和任意对角线上不能放置2个皇后），求解所有摆放方案的总数。

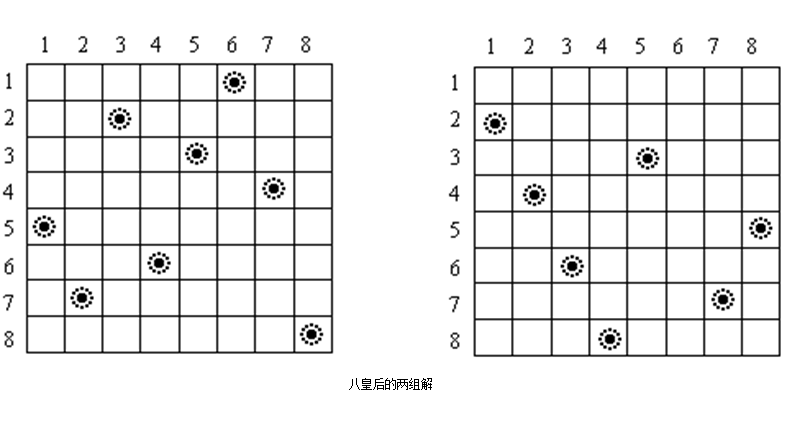
样例输入：

1

8

样例输出：

1

92

解题思路：由于皇后的摆放位置不能通过某种公式确定，因此对于每个皇后的摆放位置都要进行试探和纠正，这就是“回溯”的思想。在N个皇后为放置完成前，摆放第i个皇后和第i+1个皇后的试探方法是相同的，因此完全可以用递归的方法来处理。由于皇后的特殊性质，即一行一列只能有一个皇后，所有我们要做的就是，从第0行开始摆放，一直到摆到第n-1行为止。

关于判断当前皇后可不可以放：

我们是一行一行的放置皇后，所以不需要判断行冲突。判断列冲突很简单，直接和前面的比一下是否一样即可，而对于对角线冲突，就有一个特殊的小技巧：由于每一条主对角线（x-y）是一定的，每一条副对角线（x+y）是一定的。于是，我们通过判断那些定值与前面已经放置的皇后的定值比较即可判断是否冲突。假设我们把第x个皇后放在了第pos（x）列，那么之需要判断前x-1个皇后是否与她冲突即可。

注意：本文仅为学习DFS中一道例题，目的也仅仅是为本人更好学习DFS。但是在题目能不能AC，就不好说了，很有可能是超时的。。。

附上代码：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 int pos[];   //存储放在每行皇后的所在列的位置
 int n,ans=;
 void dfs(int x)
 //x表示放置的是第x行的皇后
 {
     if(x==n) ans++;
     else
     for(int i=;i<n;i++)
     {
         //将第x行的皇后在试着放在每一列
         int ok=;
         pos[x]=i;
         for(int j=;j<x;j++)
         {
             //判断放在第x行第i列的皇后是否和前面已经放置的皇后有冲突
             if(i==pos[j]||i+x==j+pos[j]||i-x==pos[j]-j)
             {
                 ok=;
                 break;
             }
         }
         //未找到冲突ok为1，继续放置下一行的皇后
         if(ok) dfs(x+);
     }
  }

  int main()
  {
      cin>>n;
      dfs();
      cout<<ans<<endl;
      return ;;
   }