2017 SCNUCPC 解题报告

校内赛题目、解题思路、参考代码一览

A. Blackstorm’s Blackstore

Problem Description

Blackstorm is going to open a blackstore. He now need to transport some goods.

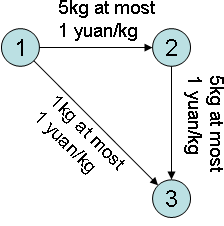
There are $n$ towns, numbered from $1$ to $n$. Goods are now at Town $1$ while the destination is at Town $n$. $m$ directed roads are connecting the towns, the $i$th of which has values $A_i, B_i, P_i, C_i$, meaning that this road connects from $A_i$th town to $B_i$th one, which can transport at most $C_i$ kilogram of goods at $P_i$ yuan per kilo. He wants to know how many goods can reach the destination with $K$ yuan.

Blackstorm is going to sleep. Can you help him solve this problem?

Input

Multiple test cases, process till end of file. For each case:

On the first line there are three numbers, $n, m, K$, described as the description says.

Following are $m$ lines, on the $i$th of which are four numbers $A_i, B_i, P_i, C_i$.

All the numbers except $K$ are integers between $[1, 100]$. $K$ is integer between $[0, 100000]$. It's also guaranteed that $A_i, B_i \leq n$.

Output

For each test case, output "Case #$T$: $ans$" (without quotes), where $T$ is the number of the cases, and $ans$ is the maximum transporting mass with 4 digits after the decimal point.

Sample Input

Sample Output

Case \#1: 3.0000

Hint

One yuan on road 1->3, two on 1->2 and two on 2->3.

解题思路

网络流版题

参考代码

#include <cstring>

#include <queue>

using namespace std;

const int MAXN = 10000;

const int MAXM = 100000;

const int INF = 0x3f3f3f3f;

struct Edge {

    int to,next,cap,flow,cost;

} edge[MAXM];

int head[MAXN],tol;

int pre[MAXN],dis[MAXN];

bool vis[MAXN];

int N;//节点总个数，节点编号从0~N-1

void init(int n) {

    N = n;

    tol = 0;

    memset(head,-1,sizeof(head));

}

void addedge(int u,int v,int cap,int cost) {

    edge[tol].to = v;

    edge[tol].cap = cap;

    edge[tol].cost = cost;

    edge[tol].flow = 0;

    edge[tol].next = head[u];

    head[u] = tol++;

    edge[tol].to = u;

    edge[tol].cap = 0;

    edge[tol].cost = -cost;

    edge[tol].flow = 0;

    edge[tol].next = head[v];

    head[v] = tol++;

}

bool spfa(int s,int t) {

    queue<int>q;

    for(int i = 0; i < N; i++) {

        dis[i] = INF;

        vis[i] = false;

        pre[i] = -1;

    }

    dis[s] = 0;

    vis[s] = true;

    q.push(s);

    while(!q.empty()) {

        int u = q.front();

        q.pop();

        vis[u] = false;

        for(int i = head[u]; i != -1; i = edge[i].next) {

            int v = edge[i].to;

            if(edge[i].cap > edge[i].flow &&

                    dis[v] > dis[u] + edge[i].cost ) {

                dis[v] = dis[u] + edge[i].cost;

                pre[v] = i;

                if(!vis[v]) {

                    vis[v] = true;

                    q.push(v);

                }

            }

        }

    }

    if(pre[t] == -1)return false;

    else return true;

}

int k;

//返回的是最大流，cost存的是最小费用

double minCostMaxflow(int s,int t) {

    int flow = 0;

    int cost = 0;

    while(spfa(s,t)) {

        int Min = INF;

        for(int i = pre[t]; i != -1; i = pre[edge[i^1].to]) {

            if(Min > edge[i].cap - edge[i].flow)

                Min = edge[i].cap - edge[i].flow;

        }

        int costper = 0;

        for(int i = pre[t]; i != -1; i = pre[edge[i^1].to]) {

            edge[i].flow += Min;

            edge[i^1].flow -= Min;

            costper += edge[i].cost;

        }

        int tmpcost = cost + costper * Min;

        if (tmpcost>=k) {

            return flow + (k-cost)/(double)costper;

        }

        cost = tmpcost;

        flow += Min;

    }

    return flow;

}

#include <cstdio>

int main() {

    int n,m,i,T=0;

    while (~scanf("%d%d%d", &n,&m,&k)) {

        init (n+2);

        for (i=0; i<m; i++) {

            int a,b,p,c;

            scanf("%d%d%d%d",&a,&b,&p,&c);

            addedge(a,b,c,p);

        }

        printf ("Case #%d: %.4f\n", ++T, minCostMaxflow(1,n));

    }

}

### B. 龟兔慢跑

Problem Description

乌龟和兔子在绕圈跑，它们同时同地出发，问出发后第一次相遇的用时。圈长$n$米，乌龟速度$w$米/分钟，兔子速度$t$米/分钟，且乌龟和兔子每跑$m$米都会休息$1$分钟再继续跑。

Input

首行一个整数$T$代表$T$组测试数据，接下来$T$行每行4个整数分别是 $n, m, t, w$。其中 $0<n<10^9$, $0<w<t<m<100$

Output

每组测试数据输出一行一个整数，表示相遇时间。测试数据保证使得相遇时间为整数。

Sample Input

1

100 100 25 20

Sample Output

Hint

64位整型long long int请使用%lld输出

解题思路

模拟

参考代码

#include <cstdio>

#include <cmath>

using namespace std;

int n,m,t,w;

void solve()

{

    int cycle=(m+t)*(m+w);

    int ds=m*(t-w);

    int cycle_num=0,dn=0;

    if(n%ds==0)

        dn=ds,cycle_num=n/ds-1;

    else

        dn=n%ds,cycle_num=n/ds;

    long long int i=0,ans=1;

    char stopw=0,stopt=0;

    double dw=0,dt=0,mw=0,mt=0;

    while(true)

    {

        i++;

        if(stopw)

            dw+=mw,stopw=0;

        else if(mw+w>=m)

            dw+=m-mw,mw=mw+w-m,stopw=1;

        else

            dw+=w,mw+=w;

        if(stopt)

            dt+=abs(mt),stopt=0;

        else if(mt+t>=m)

            dt+=m-mt,mt=mt+t-m,stopt=1;

        else

            dt+=t,mt+=t;

        /*

        printf("cycle=%d,cyclenum=%d,dn=%d,i=%I64d,dt=%f,dw=%f\n",cycle,cycle_num,dn,i,dt,dw);

        if(i%10==0){

            char s;

            scanf("%c",&s);

        }

        */

        if(abs(dn+dw-dt)<0.00001 )

        {

            ans=i+(long long int)cycle_num*cycle;

            break;

        }

        if(abs(dw-dt)<0.00001)

        {

            ans=i;

            break;

        }

    }

    printf("%I64d\n",ans);

}

int main()

{

    int T;

    scanf("%d",&T);

    while(T--)

    {

        scanf("%d%d%d%d",&n,&m,&t,&w);

        solve();

    }

    return 0;

}

### C. Snake

解题思路

瞎模拟，原题。

参考代码

无

### D. Zyj pessimistic in competition

Problem Description

There's only 10 minutes left for the ACM competition(yes the contest you're having right now). Others have already packed their pack ready to leave, while Zyj is just opening his eyes. Zyj can see how many problems any one have done, and he decided to have his rank between $(a,b)$. So how many ways are there for him? You can assume that others have penality less than 290min, so the rank of Zyj is totally decided by his answered problem, not his answering time.

Input

The first line contains an integer $T$, representing the number of tests. For each test,

There are 4 numbers $m,n,a,b$ seperated by spaces, meaning that there are $m$ problems in this test($0<m<27$ due to the number of letters) and $n$ participants other than Zyj himself. Zyj's rank should fall in $(a,b)$.

The following line shows how many seconds Zyj needs to solve each problem(for each time $t$, $0 \leq t < 999$, and t have at most 6 digits after the decimal point).

Next are $n$ lines, each contain $m$ numbers, the $j$th number on the $i$th line showing whether the $i$th man have solved the $j$th problem, where 1 means he did and 0 means he didn't.

Output

For each test case, output Case #k: $Ans$, which means that in the $k$th case there are $Ans$ ways.

Sample Input

1

4 1 0 2

300 300 300 300

0 0 0 1

Sample Output

Case \#1: 6

Hint

For a rank in $(0,2)$, or say the first, Zyj needs to solve 2 problems at least. Since he needs 5 minutes (300 s) to solve one, he can only solve 2 in 10 minutes. Thus there are $C_4^2=6$ ways.

解题思路

原题改改又是一年，二分。

参考代码

出题人的代码太丑了，我不敢放上来。

### E. How many LLM

Problem Description

LLM is also known as L2M. Find out how many of them are there.

Input

Multiple test cases, one per line.

On each line is a string. You need to find out how many LLM(L2M) are there. LLM(L2M)s needn't be continious, but any two can't overlap.

Output

One number per test cases, indicating how many LLM(L2M) are there at most.

Sample Input

LLL2MM

2LLLMM

Sample Output

2

1

解题思路

从后往前遍历，为每个M找L。如果先找到2可以当L用，凑够两个就消掉了。

参考代码

#include <stdio.h>

#include <string.h>

char str[10000007];

int main() {

    while (gets(str)) {

        int L=strlen(str), i, m=0, n=0, t=0;

        for (i=L; i--; ) {

            if (str[i] == 'M')

                m++;

            if (str[i] == '2' && m)

                m--, t++;

            if (str[i] == 'L') {

                if (t) {

                    t--;

                    n++;

                } else if (m)

                    t++, m--;

            }

        }

        printf ("%d\n", n);

    }

}

### F. Fabonacci

Problem Description

我们知道Fabonacci数组通项函数定义如下：

$F(1)=1,F(2)=2$

$F(N)=F(N-1)+F(N-2), N>2$

现在给你$M$个各不相同的正整数$A_1,A_2,\cdots,A_M$，问你能不能找到一个正整数$S$使得$F(S)=F(A_1)+F(A_2)+\cdots+F(A_M)$。

Input

第一行输入一个整数$T$，表示有$T$组测试数据。对于每一组测试数据，第一行是一个正整数$M$，第二行是$M$个正整数$A_1,A_2,\cdots,A_M$。

$0<M<10000$

$0<A_i<1000000$

Output

输出有$T$行，每一行对应一组测试数据。

对于每组测试数据，如果能找到满足的$S$,则输出$S$，否则输出$-1$。

Sample Input

Sample Output

6

-1

解题思路

首先注意：$M$个不各不相同的正整数。如果存在相同，或者在模域上求，则是难度更大的解法。
性质：$F(A_M) < F(S) < F(A_M+2)$，即当有解时只可能为$S = A_M + 1$。
证明：
1. 显而易见得，$F(S) > F(A_M)$，且$F(S) = \sum_{i=1}^{M} F(A_i) < \sum_{i=1}^{A_M} F(i)$；
2. $\sum_{i=1}^{N} F(i) = 1+F(1)+F(2)+\cdots+F(N)-1 = F(2)+F(1)+F(2)+\cdots+F(N)-1$；
3. $\sum_{i=1}^{N} F(i) = F(3)+F(2)+F(3)+\cdots+F(N)-1 = \cdots = F(N)+F(N-1)+F(N)-1 = F(N+2) - 1$；
4. 所以$F(A_M) < F(S) < F(A_M+2)-1 < F(A_M+2)$，根据夹逼法则，$S$只可能存在唯一解$S = A_M + 1$。
推理：$F(S)=F(A_M)+F(A_M-1)=F(A_M)+F(A_M-2)+F(A_M-3)=\cdots$，可知若$S$有解，则数列$A$必须满足前两项相差$1$，后面的项与前一项相差$2$。
贪心：由于数列$A$各不相同，设有序，则只有当$A_1+1=A_2$时，$F(A_1)$和$F(A_2)$可加（否则不能解出$S=F^{-1}(F(S))$）；设相加结果为$A_i'(i \geq 2)$，同理只有当$A_i'+1=A_{i+1}$时其在$F$上的像可加。因此每次取最小两个$A_x$相加能得到全局解$S$，若存在一次不可加（即最小两个$A_x$相差大于$1$），则调整前面任何一个都不能与之相加，选取后面不相邻的任何一个都不能与之相加；特殊情况时数列$A$及其子数列可划分为两部分各自可加，由于前部分最大值和后部分最小值相差大于$1$，因此两部分整体不可加，由此得证贪心法正确性。
时间复杂度：$O(MlogM + M)$

出题人提供的题解

不失一般性的，我们可以假设$A_1<A_2<\cdots<A_M\leq S$。
由于$F(S)=F(S-2)+F(S-3)+\cdots+F(2)+F(1)+2$
假设$S>A_M+1$，则明显有$F(S)\neq F(A_1)+F(A_2)+\cdots+F(A_M)$，假设不成立。
假设$S=A_M$，则只有$M=1$时才成立。
假设$S=A_M+1$，使$F(S)=F(A_1)+F(A_2)+\cdots+F(A_M)$满足的充分必要条件是$F(A_M-1)=F(A_1)+F(A_2)+\cdots+F(A_{M-1})$。如此不断归约，问题最终会化为$F(A_3-1)=F(A_1)+F(A_2)$。
综合上面的式子，得到满足条件$F(A_1)=F(A_2)=F(A_3-1),F(A_3-1)+F(A_3)=F(A_4-1)$。即应该满足$A_1=A_2-1,A_2=A_3-2,\cdots,A_{M-1}=A_M-2$。

参考代码

#include <cstdio>

int main() {

    scanf("%d", &t);

    while(t--) {

        scanf("%d", &n);

        for(int i = 0; i < n; ++i) scanf("%d", a + i);

        if(n < 2) printf("%d", a[0]);

        else {

            sort(a, a  + n);

            bool flag = true;

            int ans;

            if(a[0] == a[1] - 1) {

                ans = a[1] + 1;

                for(int i = 2; i < n; ++i)

                    if(ans == a[i] - 1)

                        ans = a[i] + 1;

                    else flag = false;

            } else flag = false;

            if(flag) printf("%d\n", ans);

            else puts("-1");

        }

    }

    return 0;

}

### G. 保龄球

Problem Description

Oyk开了一个保龄球馆，馆中有$N$个保龄球瓶一字排开，每个保球瓶都有一个固定的权值，它们分别是$A_1,A_2,\cdots,A_N$。每次掷出一个保龄球只会打倒一个保龄球瓶，假如打倒的是第$i$个保龄球瓶，则得到的分数为它与相邻两个没有被倒下的保龄球瓶共三个权重的乘积，即$A_{i-1}*A_i*A_{i+1}$，然后第$i-1$与第$i+1$个保龄球瓶就变成相邻的了。(当然，打倒最前或最后的瓶得到的分数只有两个数的乘积，打倒剩下的最后一个瓶得到的分数即为它本身的权重)。现在给你$N$个保龄球瓶的权重，问不同的打倒方案中能达到的最高得分是多少？

Input

输入数据的第一行为一个正整数$T$，代表着测试数据数量。对于每一个测试数据，第一行为一个正整数$N$，代表着保龄球瓶的数量。第二行为$N$个正整数$A_1,A_2,\cdots,A_N$，按顺序表示这$N$个保龄球瓶的权重。

$0<N<100$

$0<A_i<100$

Output

输出数据总共有$T$行，每一行对应一个测试数据。对于每一个测试数据，输出一个正整数，表示能达到的最大总得分。

Sample Input

Sample Output

解题思路

DP。
时间复杂度：$O(N^3)$

参考代码（出题人的代码）

#include <cstdio>

#include <cstring>

#include <iostream>

using namespace std;

int a[200];

int dp[200][200];

int main() {

    int t, n;

    scanf("%d", &t);

    while(t--) {

        scanf("%d", &n);

        memset(dp, 0, sizeof(dp));

        a[0] = a[n + 1] = 1;

        for(int i = 1; i <= n; ++i) scanf("%d", a + i);

        for(int k = 0; k < n; ++k)

            for(int l = 1; l + k <= n; ++l) {

                int r = l + k;

                for(int mid = l; mid <= r; ++mid)

                    dp[l][r] = max(dp[l][r], dp[l][mid - 1] + a[l - 1] * a[mid] * a[r + 1] + dp[mid + 1][r]);

            }

        printf("%d\n", dp[1][n]);

    }

    return 0;

}

### H. 淹水

Problem Description

某地区有两个山峰。某年由于洪水，高的山峰被淹了两次，而低的山峰只被淹了一次。有可能吗？

答：有可能。在一次洪水淹了高的山峰，退去时低的山峰尚未露出水面，水位就又上升淹了高处山峰。

现在给出若干个山峰的高度和淹没次数，问这个次数可能出现吗？

Input

输入有多组数据，处理到文件尾。每组数据中，第一行为$N$，山峰数量，下面$N$行分别有两个数字$A, B$，表示一座高度为$A$的山峰被淹了$B$次。

$0 \leq A, B, N < 10000$

Output

如果可能，输出YES；否则输出NO。

Sample Input

Sample Output

YES

解题思路

水题。原定是签到题。
先从小到大排个序，1. 如果前面的山峰没被淹过，后面高的山峰就不可能被淹；2. 如果相同高度的山峰被淹次数不等，则不可能。

参考代码

#include <stdio.h>

#include <algorithm>

using std::sort;

int N;

struct Mountain {

    int height, count;

    bool operator<(const Mountain&c)const {

        return height < c.height;

    }

}mountain[10010];

void read() {

    for (int i = 0; i < N; ++i)

        scanf("%d%d", &mountain[i].height, &mountain[i].count);

}

int judgeEqual(int idx) {

    return mountain[idx].height != mountain[idx-1].height

        || mountain[idx].count == mountain[idx-1].count;

}

int judgeImpossible(int idx) {

    return mountain[idx-1].count == 0 && mountain[idx].count > 0;

}

int work() {

    sort(mountain, mountain+N);

    int eqFlag = 1, impFlag = 0;

    for (int i = 1; i < N; ++i) {

        eqFlag = judgeEqual(i);

        if (!eqFlag) return 0;

        impFlag = judgeImpossible(i);

        if (impFlag) return 0;

    }

    return 1;

}

int main() {

    while (~scanf("%d", &N)) {

        read();

        puts(work()? "YES": "NO");

    }

    return 0;

}

出题及解题总结

复盘

我没参与出题，因为我太蠢了。
想要复盘整个过程，也有很多话想说，最终还是按下了无数次退格。
嗨呀，大家都辛苦了啊！

建议、意见、吐槽

欢迎在下方评论区提出问题，4月内我都会回复and更新。

本文基于知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议发布，欢迎引用、转载或演绎，但是必须保留本文的署名BlackStorm以及本文链接http://www.cnblogs.com/BlackStorm/p/SCNUCPC_2017_Solution.html，且未经许可不能用于商业目的。如有疑问或授权协商请与我联系。