逻辑回归LR

逻辑回归算法相信很多人都很熟悉，也算是我比较熟悉的算法之一了，毕业论文当时的项目就是用的这个算法。这个算法可能不想随机森林、SVM、神经网络、GBDT等分类算法那么复杂那么高深的样子，可是绝对不能小看这个算法，因为它有几个优点是那几个算法无法达到的，一是逻辑回归的算法已经比较成熟，预测较为准确；二是模型求出的系数易于理解，便于解释，不属于黑盒模型，尤其在银行业，80%的预测是使用逻辑回归；三是结果是概率值，可以做ranking model；四是训练快。当然它也有缺点，分类较多的y都不是很适用。下面我先具体介绍下这个模型。

一、逻辑回归LR介绍

首先要搞清楚当你的目标变量是分类变量时，才会考虑逻辑回归，并且主要用于两分类问题。举例来说医生希望通过肿瘤的大小x1、长度x2、种类x3等等特征来判断病人的这个肿瘤是恶性肿瘤还是良性肿瘤，这时目标变量y就是分类变量（0良性肿瘤，1恶性肿瘤）。显然我们希望像保留像线性回归一样可以通过一些列x与y之间的线性关系来进行预测，但是此时由于Y是分类变量，它的取值只能是0,1,或者0,1,2等等，不可能是负无穷到正无穷，这个问题怎么解决呢？此时引入了一个sigmoid函数，这个函数的性质，非常好的满足了，x的输入可以是负无穷到正无穷，而输出y总是[0,1]，并且当x=0时，y的值为0.5，以一种概率的形式表示. x=0的时候y=0.5 这是决策边界。当你要确定肿瘤是良性还是恶性时，其实我们是要找出能够分开这两类样本的边界，叫决策边界。

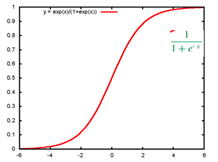
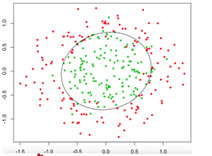
而通过sigmoid函数，可以将我们喜欢的线性表示的函数嵌入其中，当theta*x得到的值大于0，则h(x)得到的概率值大于0.5时，表明属于该分类；当theta*x得到的值小于0，则h(x)小于0.5时表示不属于该分类。这样也就形成了我们看到的逻辑回归，具体如下：

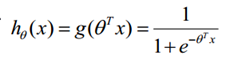
其中theta是向量，

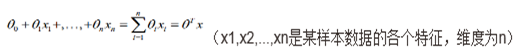
二、逻辑回归估计（最小化损失函数loss function）

损失函数是在机器学习中最常出现的概念，用于衡量均方误差[（模型估计值－模型实际值）^2／ n]最小，即预测的准确性，因而需要损失函数最小，得到的参数才最优。（线性回归中的最小二乘估计也是由此而来）但因为逻辑回归的这种损失函数非凸，不能找到全局最低点。因此，需要采用另一种方式，将其转化为求最大似然，如下，具体的推导求解过程可参见博客http://blog.csdn.net/suipingsp/article/details/41822313 另一种较为好理解的方式是，如果Y=1，你胆敢给出一个h(x)很小的概率比如0.01，那么损失函数就会变得很大：

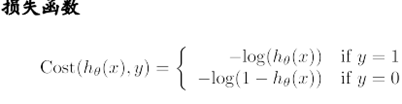
此时的损失函数变成了凸函数，Theta的求解，就是梯度下降法求最小值，此时加入的正则化项，是解决过拟合问题。（过拟合问题：如果我们的模型有非常多的特征，模型很复杂，模型对原始数据的拟合效果很好，但是丧失一般性，对新的待预测变量预测效果很差。（听过寒小阳老师举过一个很好理解的例子，就是这个学生只是强硬的记住题目，并没有掌握规律，高考不一定考的好）怎么解决呢？限制参数寺塔，损失函数加上关于theta的限制，即如果theta太多太大，则就给予惩罚。L2正则化。）

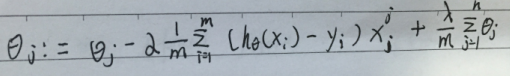
该公式将一直被迭代执行，直至达到收敛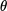（（）在每一步迭代中都减小，如果某一步减少的值少于某个很小的值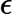（）（小于0.001）, 则其判定收敛）或某个停止条件为止（比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围）。 转换为向量的处理方法同样可参见上文博客：http://blog.csdn.net/suipingsp/article/details/41822313

三、LR应用经验

如果连续变量，注意做SCALING，缩放单位即标准化。LR对样本分布敏感，所以要注意样本的平衡性（y=1不能太少）样本量足的情况下采用下采样，不足的情况用上采样。

LR对于特征处理非常重要，常用处理手段包括，通过组合特征引入个性化因素(FM,FFM)；注意特征的频度；聚类、HASH。但LR不怕特征大，GBDT比较怕。对于连续变量的离散化，可以用CART查看离散的结果，生成新的特征，再用LR。

LR和FM对于稀疏高维特征处理是无压力的，GBDT对于连续值自己会找到合适的切分点，xgboost也可以处理category类型的feature，无需one-hot，平展开的高维稀疏特征对它没好处。

算法调优方面，选择合适的正则化，正则化系数，收敛阈值e，迭代轮数，调整loss function给定不同权重；bagging或其他方式的模型融合；最优算法选择（‘newton-cg’,’lbfgs’, ‘liblinear’）；bagging或其他模型融合。Sklearn中的LR实际上是liblinear的封装。

LR和SVM对于线性切分都有着比较好的表现，对于非线性切分，必须在原始数据上做一些非线性变换。LR必须做feature mapping，比如把X做个平方项，X1*X2等；SVM则需要利用核函数

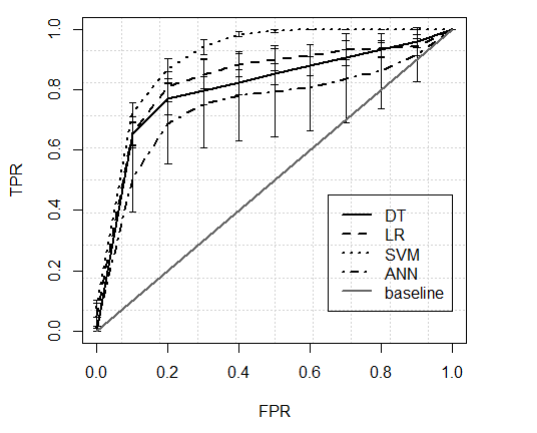
模型的评价主要用ROC曲线。ROC（接受者操作特征）曲线实际上是对概率输出设置了一个门槛D，当P(C|x)>D时，事件C为真，  而ROC曲线反映了，在一系列可能门槛值下，真正率（ TPR）和假正率(FPR)的值，一个好的模型必须在一个高的真正率（ TPR）和一个低的假正率(FPR)中取得一个折衷水平，ROC曲线下的面积越大越好，最大为1.