NOIP2016 T4 魔法阵 暴力枚举+前缀和后缀和优化

想把最近几年的NOIP T4都先干掉，就大概差16年的，所以来做一做。

然后这题就浪费了我一整天QAQ...果然还是自己太弱了QAQ

点我看题

还是pa洛谷的...

题意：给m个物品，每个物品有一个不超过n的数xi。

如果存在四元组 (a,b,c,d)满足

①        x_a<x_b<x_c<x_d

　　②　　 x_b-x_a=2(x_d-x_c)

③       x_b-x_a<(x_c-x_b)/3

辣么这个四元组是有效的，问每个物品分别作为有效四元组中 a，b，c，d 几次

思路：16年是第一次参加的noip啊...结果炸的挺惨的，比赛的时候这题没多少时间打了，就草草打了一个暴力优化，结果细节没考虑挂掉了。

今天再来写的时候先敲了暴力，一个简单的暴力优化可以水到85分，所以真的是暴力出奇迹啊=v=

辣正解捏，不得不说这题的数学成分实在太高，我想了整整一个下午都没搞懂，但其实真的不是很难吧...

我们可以这样去想，把每一个物品的数字都抽象为一个数轴上的点的坐标。

然后画图。

可以这样考虑，设x_d-x_c=i 则 x_b-x_a=2*(x_d-x_c)=2*i

把化简的二式带入三式 得：  6*i<x_c-x_b  设6*i+k=x_c-x_{b   ( 就是把差的部分补上去，这个姿势貌似还挺有用)}

这样的话就可以画图了，由一式条件和化简后的式子可以得到这样的图

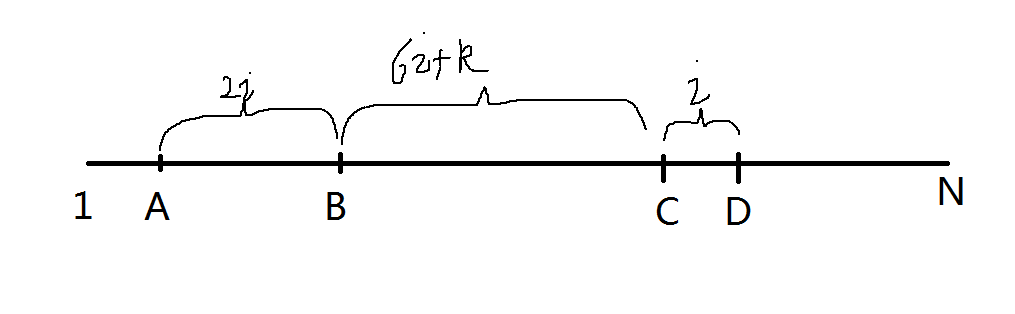
图丑就别喷了...  所以 AD=9i+k 所以 i 的取值范围也可以得到 1≤i≤n/9 (准确来说 i 要比n更小，不过没什么影响)

画完图是不是清晰了一点(其实并没有啊)

然后我萌就可以这样想了，如果知道了 i  和 A 就可以得到 B    如果知道  i  和 C 就可以得到 D  但是如果仅知道某两项是得不到其他的。

我萌把A和B看成一个整体，把C和D看成一个整体，并分别求答案。

我萌枚举 i ，然后枚举 A  这样可以算出 B， 同时 我萌可以知道 C 和 D的最小位置 即当 k=1 时 C=A+8i+1，D=A+9i+1, 知道这个最小位置有什么用？

因为知道A的答案=数字为B的物品个数*数字为C的物品个数*数字为D的物品个数

而对于任意k，如果存在数字C的位置有物品且D的位置有物品，辣么很显然 数字为C的物品个数*数字为D的物品个数 可以通过枚举A的过程中利用后缀和进行累积，然后又因为要后缀和，所以A就得从后往前枚举。

B的答案类似，在A进行求答的时候可以一起求了。

B的答案=数字为A的物品个数*数字为C的物品个数*数字为D的物品个数

辣CD为一个整体的时候捏，类比啊，一样的，但是发现数字为A的物品个数*数字为B的物品个数 累积的时候是前缀和了，所以C的枚举就是从前往后。

一道很棒的题，很棒的数学题...(困惑了我好久，看题解还看不懂！！)

 var n,m:longint;
     a,id,num:array[..]of longint;
     l:array[..]of longint;
     i,j,k,d:longint;
     z:longint;
     numab,numcd:longint;
     sum:array[..,..]of longint;
 begin
   read(n,m);
   for i:= to m do
   begin
     read(a[i]);
     inc(num[a[i]])
   end;
   for i:= to (n div ) do
   begin
     numcd:=;
     for j:=n-(*i+) downto  do
     begin
       numcd:=numcd+num[j+*i+]*num[j+*i+];
       inc(sum[j,],num[j+*i]*numcd);
       inc(sum[j+*i,],num[j]*numcd);
     end;
     numab:=;
     for j:=*i+ to n-i do
     begin
       numab:=numab+num[j-*i-]*num[j-*i-];
       inc(sum[j,],num[j+i]*numab);
       inc(sum[j+i,],num[j]*numab);
     end;
   end;
   for i:= to m do
   begin
     for j:= to  do
     write(sum[a[i],j],' ');
     writeln;
   end;
 end.

NOIP2016 T4

转c++后重新写了一遍这题，有了更好的理解代码一起pia上来

 #include<cstdio>
 #define ll long long
 using namespace std;
 ll ans[][];
 int a[],num[];
 int main(){
     int n,m;
     scanf("%d%d",&n,&m);
     for (int i=;i<=m;i++){
         scanf("%d",&a[i]);
         num[a[i]]++;
     }
     for (int t=;t<=n/;t++){
         ll sum=;
         for (int i=*t+;i<=n-t;i++){
             sum+=1ll*num[i-*t-]*num[i-*t-];
             ans[i][]+=sum*num[i]*num[i+t];
             ans[i+t][]+=sum*num[i]*num[i+t];
         }
         sum=;
         for (int i=n-*t-;i>*t;i--){
             sum+=1ll*num[i+*t+]*num[i+*t+];
             ans[i][]+=sum*num[i]*num[i-*t];
             ans[i-*t][]+=sum*num[i]*num[i-*t];
         }
     }
     for (int i=;i<=m;i++){
         for (int j=;j<=;j++)
         printf("%lld ",ans[a[i]][j]/num[a[i]]);
         printf("\n");
     }
     return ;
 }
 /*
 条件① Xa<Xb<Xc<Xd
     ② Xb-Xa=2(Xd-Xc)
     ③ Xb-Xa<(Xc-Xb)/3
     可以发现Xd-Xc是一个最小单位
     设 t=Xd-Xc;
     ②得Xb-Xa=2t
     ③得2t<(Xc-Xb)/3 即6t<Xc-Xb
     粗略的画图
     --------------------
      A B------C  D
      --- >6t  ----
       t        2t
     D最大是n A最小是1
     所以t的取值就是
     1<=t<=(n-1)/t
     粗略的
     1<=t<=n/t 因为数组开大后溢出没有任何影响
     于是枚举t 再枚举C
     D的位置就得到了
     而因为BC之间只要大于6t就行。
     所以设C1<C2 D1<D2
     C1 D1所能匹配的A B C2 D2 也可以
     于是满足了前缀和
     只要往后枚举C的时候把上一个C的A B组数保存着累加就好了
     A B同理，枚举 B，A确定 C D变成了后缀和。
     画图把B C的取值范围算一下即可
 */ 

NOIP2016 T4

果然自己真的要多做题啊QAQ