洛谷 2633 BZOJ 2588 Spoj 10628. Count on a tree

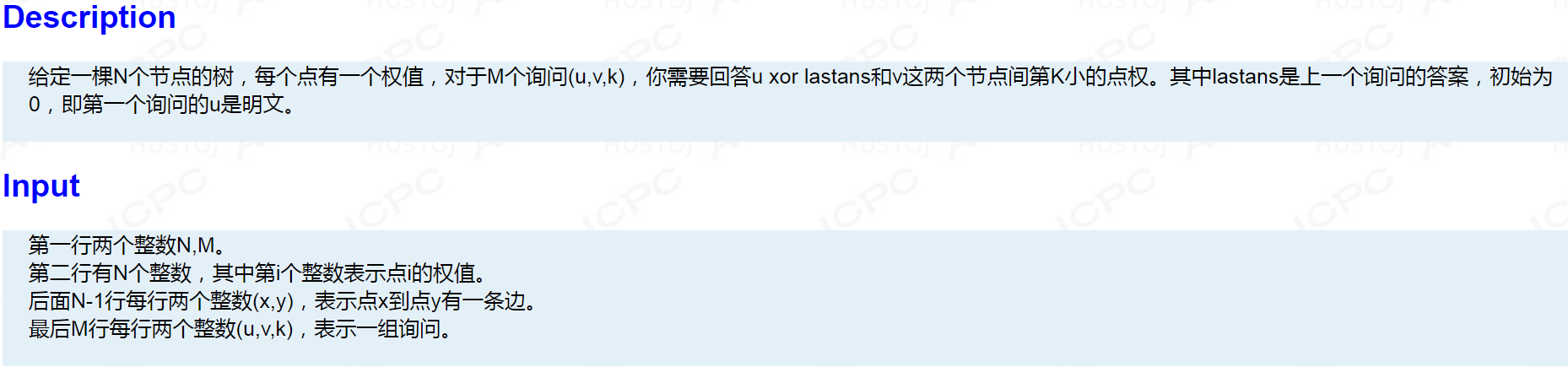
【题解】

　　蜜汁强制在线。。。

　　每个点开一个从它到根的可持久化权值线段树。查询的时候利用差分的思想在树上左右横跳就好了。

　　

 #include<cstdio>
 #include<algorithm>
 #define N 100010
 #define rg register
 #define ls (a[u].l)
 #define rs (a[u].r)
 using namespace std;
 int n,n2,m,tot,root[N],last[N],dep[N],top[N],hvy[N],fa[N],size[N],val[N],b[N];
 struct tree{
     int sum,l,r;
 }a[N*];
 struct edge{
     int to,pre;
 }e[N<<];
 inline int read(){
     int k=,f=; char c=getchar();
     while(c<''||c>'')c=='-'&&(f=-),c=getchar();
     while(''<=c&&c<='')k=k*+c-'',c=getchar();
     return k*f;
 }
 inline int qlca(int x,int y){
     int f1=top[x],f2=top[y];
     while(f1!=f2){
         if(dep[f1]<dep[f2]) swap(x,y),swap(f1,f2);
         x=fa[f1]; f1=top[x];
     }
     return dep[x]<dep[y]?x:y;
 }
 void update(int &u,int l,int r,int pos){
     a[++tot]=a[u]; a[u=tot].sum++;
     if(l==r) return;
     int mid=(l+r)>>;
     if(pos<=mid) update(ls,l,mid,pos);
     else update(rs,mid+,r,pos);
 }
 int query(int u,int v,int lca,int f,int l,int r,int k){
     if(l==r) return l;
     int tmp=a[ls].sum+a[a[v].l].sum-a[a[lca].l].sum-a[a[f].l].sum,mid=(l+r)>>;
     return k<=tmp?query(ls,a[v].l,a[lca].l,a[f].l,l,mid,k):query(rs,a[v].r,a[lca].r,a[f].r,mid+,r,k-tmp);
 }
 void dfs1(int x){
     size[x]=; dep[x]=dep[fa[x]]+;
     root[x]=root[fa[x]]; update(root[x],,n2,val[x]);
     for(rg int i=last[x],to;i;i=e[i].pre)if((to=e[i].to)!=fa[x]){
         fa[to]=x; dfs1(to);
         size[x]+=size[to];
         if(size[to]>size[hvy[x]]) hvy[x]=to;
     }
 }
 void dfs2(int x,int tp){
     top[x]=tp;
     if(hvy[x]) dfs2(hvy[x],tp);
     for(rg int i=last[x],to;i;i=e[i].pre)
         if((to=e[i].to)!=fa[x]&&to!=hvy[x]) dfs2(to,to);
 }
 int main(){
     n=read(); m=read();
     for(rg int i=;i<=n;i++) val[i]=b[i]=read();
     sort(b+,b++n); n2=unique(b+,b++n)-b-;
     for(rg int i=;i<=n;i++) val[i]=lower_bound(b+,b++n2,val[i])-b;
     for(rg int i=;i<n;i++){
         int u=read(),v=read();
         e[++tot]=(edge){v,last[u]}; last[u]=tot;
         e[++tot]=(edge){u,last[v]}; last[v]=tot;
     }
     tot=; dfs1(); dfs2(,);
     int last=;
     while(m--){
         int u=read()^last,v=read(),k=read(),l=qlca(u,v),f=fa[l];
         printf("%d\n",last=b[query(root[u],root[v],root[l],root[f],,n2,k)]);
     }
     return ;
 }