前缀和小结 By cellur925

这篇主要是来介绍前缀和的QAQ。

前缀和有一维的和二维的，一维的很容易理解，高中数学必修5第二章数列给出了前n项和的概念，就是前缀和。一维的我们在这里简单说一句。

一维前缀和

预处理：在输入一个数列的时候累加

查询区间和：查询[i,j]区间全部元素的和--sum[j]-sum[i-1]

二维前缀和

预处理：用到了容斥原理的知识。即求矩阵左上角的顶点与当前点所围成的矩形所覆盖的权值。

设f[][]为前缀和数组，则f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j]

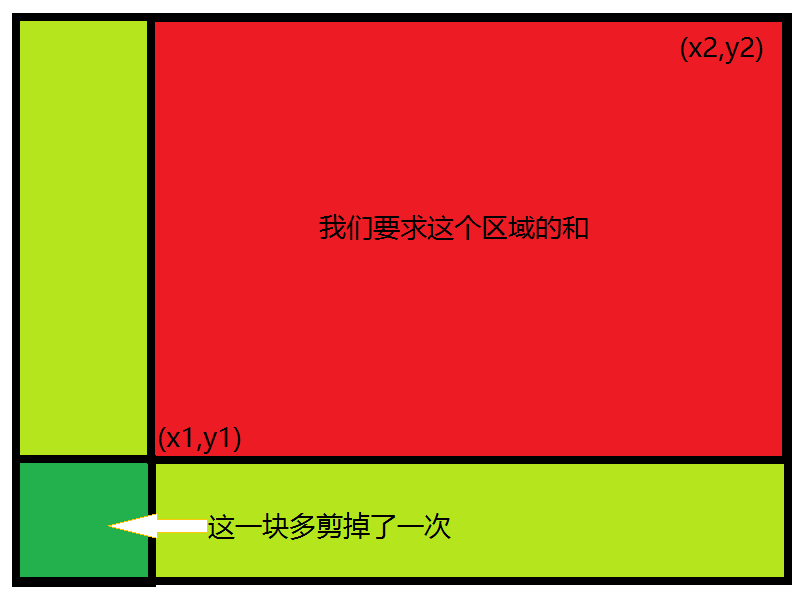
（注：图片来源@ShawnZhou 神犇，原文地址，感谢，侵删。）

查询区间和：

　　对于一个边长为R的正方形，以(i,j)作为右下角的，那它矩阵中的和为

　　s[i][j]-s[i-R,j]-s[i,j-R]+s[i-R,j-R]

放两道例题跑（

例题1 [HNOI2003]激光炸弹

前缀和+枚举边长

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 int n,R,ans;
 int f[][];
 int main()
 {
     scanf("%d%d",&n,&R);
     for(int i=;i<=n;i++)
     {
         int x=,y=,z=;
         scanf("%d%d%d",&x,&y,&z);
         f[x+][y+]=z;
     }
     for(int i=;i<=;i++)
      for(int j=;j<=;j++)
      {
          f[i][j]+=f[i-][j]+f[i][j-]-f[i-][j-];
      }
     for(int i=;i<=-R;i++)
      for(int j=;j<=-R;j++)
      {
          int tmp=f[i+R][j+R]-f[i+R][j]-f[i][j+R]+f[i][j];
          ans=max(tmp,ans);
      }
     printf("%d",ans);
     return ;
 } 

例题2 最大正方形

可能是隐藏在dp标签下的一个叛徒这题我觉得用前缀和最简单，而且还是01矩阵，只要预处理出前缀和然后枚举最大正方形的边长大小，再看矩阵中权值和是否等于边长*边长即可。以及注意边界问题。

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int n,m,ans;
 int f[][];

 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
         {
             scanf("%d",&f[i][j]);
             f[i][j]+=f[i-][j]+f[i][j-]-f[i-][j-];
         }
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             for(int k=;k<=max(n,m);k++)
             {
                 if(i-k<) continue;
                 if(j-k<) continue;
                 int qwq=f[i][j]-f[i-k][j]-f[i][j-k]+f[i-k][j-k];
                 if(qwq==k*k) ans=max(ans,k);
             }
     printf("%d",ans);
     return ;
 }

---

*update on 10-18

noip2014无线网络发射器选址

二维前缀和裸题，当然也可直接枚举中心统计。

但是发现自己前缀和这理解可能有点问题hhh。

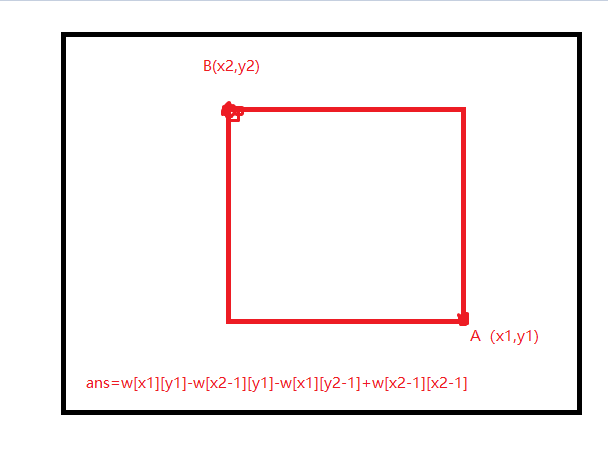
其实是这样的qwq。（当然变量名不能用x1y1之类的啦）

 #include<cstdio>
 #include<algorithm>
 #include<iostream> 

 using namespace std;
 typedef long long ll;

 int d,n;
 ll tot,ans;
 ll w[][];

 int main()
 {
 //    freopen("1.out","w",stdout);
     scanf("%d%d",&d,&n);
     for(int i=;i<=n;i++)
     {
         int x=,y=,z=;
         scanf("%d%d%d",&x,&y,&z);
         w[x][y]=z;
     }
     for(int i=;i<=;i++)
         for(int j=;j<=;j++)
             w[i][j]+=w[i-][j]+w[i][j-]-w[i-][j-];
     for(int i=;i<=;i++)
         for(int j=;j<=;j++)
         {
             //if(i-d<0||i+d>128||j-d<0||j+d>128) continue;
             int tx=(i+d<=) ? (i+d) : ;
             int ty=(j+d<=) ? (j+d) : ;
             int lx=(i-d>=) ? (i-d) : ;
             int ly=(j-d>=) ? (j-d) : ;
             ll tmp=w[tx][ty]-w[tx][ly-]-w[lx-][ty]+w[lx-][ly-];
             //if(i==120&&j==120) cout<<tx<<" "<<ty<<" "<<lx<<" "<<ly;
             //if(i==120&&j==120) cout<<tmp;
             if(tmp>ans) ans=tmp,tot=;
             else if(tmp==ans) tot++;
         }
     printf("%lld %lld",tot,ans);
     return ;
 }