校内测之zay与银临 (day2)（只有T1）

一些与题目无关的碎碎念

推出式子来一定要化简!!!freopen不要写错!!!特判不要瞎搞!!!!

据说fropen没写（注释掉）可以卡zay的评测机1min

做到以上三点能高35分qwq

一篇我也不知道说了些什么的题解总之锅很大

T1 江城唱晚

zayの题解

你看数据那么大，显然又是一道数学题。

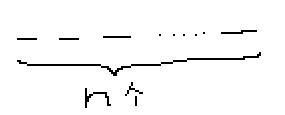
这里有n个种海棠的坑，我们要种m个（还不能挨着种，虽然不知道是什么原理）

那我们不妨先把不种海棠的坑那出来，最后再差回去

如果拿出来的坑的数量还不够m,最后肯定无法保证每两棵海棠之间至少隔1个空，这就是无解情况。然而数据保证有解，就不特判了（只是因为懒）。

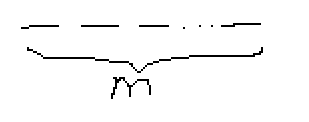
现在只有m个坑了。因为编号不同的花种在同一位置也是一种新的方案，所以这m棵花的所有排列方式是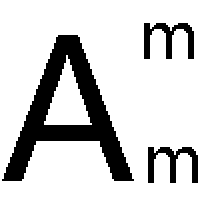种，由公式得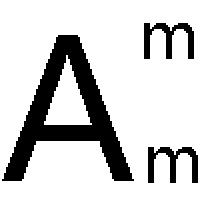=m!

我们再把拿出来的n-m个坑差回去。因为n-m>=m,所以我们倒着来，把m个有花的坑插在n-m+1个地方。

解释一下为什么是n-m+1

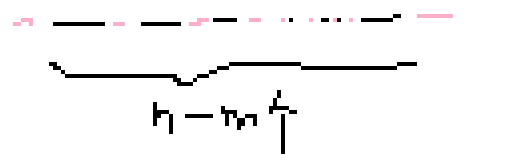
其中，黑色的是不种花的坑，粉色的是种花的坑可以放的地方

在n-m+1个空中任选m个的方案数是什么呢？

zhx的小学老师说是个

综上，方案数：

 

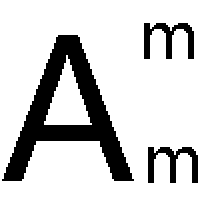
也就是  (n-m+1)!/(m!*(n-2m+1)!*m!

化简一下:(n-m+1)!/(n-2m+1)!=(n-2m+2)*(n-2m+3)*.....*(n-m+1)

似乎没法再化简了，那就暴力乘起来呗

就有了代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
long long m,mod,n,type,ans=;
inline long long read()
{
    char ch=getchar();
    long long x=;bool flag=;
    while(ch<''||ch>'')
    {
        if(ch=='-')flag=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    if(flag)x=-x;
    return x;
}
int main()
{
    freopen("ilove.in","r",stdin);//别写错了
    freopen("ilove.out","w",stdout);
    type=read();n=read();m=read();mod=read();//既然type自己觉得没有什么用就不要乱特判了
     for(int i=n-*m+;i<=n-m+;i++)
      ans=ans*i%mod;
    printf("%lld",ans);
    return ;
}

T2:不老梦

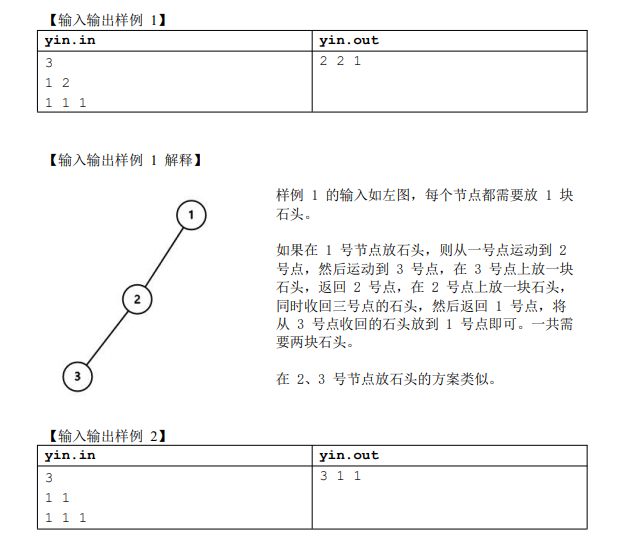
zayの题解：

（有关爆搜的代码并不会写）

我们还是从特殊情况开始看

n=1，只要写freopen就有5分（连freopen都没有写的人不想说话）

n=8，zay曾经说过小数据就是用来搜索的。我们搜索出来所有合法的放石子的顺序就ok了

搜索小技巧：在搜索过程中，如果可以判定无解，就不要搜索了，即在搜索树上有儿子的节点一定可以搜到答案

n再大一点，我们看到了二叉树

对于二叉树，只要把走两个儿子产生的结果比较一下，选取最小的即可（蒟蒻不会写代码）

孩子节点不超过5的子任务和二叉树做法差不多（反正我也不会）

我们迎来了最后一个特殊性质：树高不超过3

这个性质有什么用吗？没有卵用

肯定是有用的。废话。我们来看一棵树

对于叶子节点，ansi=wi.我们再截取一部分

设1的每个孩子都有一个ans值，ansi代表i点需要的石头，wi代表i的权值

设走完所有儿子的需要的石子为x,w2+w3+w4+w5=y,x-y=rest

若rest>=w1,则ans1=x,因为rest即为收回2,3,4,5的孩子的石子的数量

若rest<w1,那么ans1=x+w1-rest=x+w1-(x-y)=x+w1-x+y=w1+y,也就是1的权值加上它孩子的权值

我们要让ans1尽可能的小，所以就要让x尽可能的小（当rest<w1的时候，ans1就是定值了）

因为子节点遍历的顺序是任意的，所以先走哪个节点都是合法的。这时候问题就转化成了上面zay题解的形式，即有x个物品，每个物品花wi元，但购买时要求持有ansi元，求一个顺序，使最终花费最小（在购买过程中如果出现持有的现金不够ansi元的情况，则要增加最终花费）

那怎么选呢？显然zay告诉你了对不对，就是按照ansi-wi进行不升序排序，然后选。

证明：我们设ai=ansi-wi,aj=ansj-wj.且ai>aj

先买i的消费：max(ansi,ansj+wi)。若买完i剩下的钱（ai）足够买j,就用剩下的钱买j，此时总的花费是ansi,若ai不够买j,就需要再补上ansj-ai元，那么总数就是ansi+ansj-ai=ansj+wi元

我们对这个式子进行化简：max(ansi,ansj+wi)=wi+max(ai,aj+wj)①

再来看先买j再买i的消费：max(ansj,ansi+wj)（同理可得）

化简一下：max(ansj,ansi+wj)=wj+max(aj,ai+wi)②

将①和②比较一下，如果①式取的是ai,则先买i的花费是ansi,此时先买j的代价是ansi+wj(ai>aj+wj,则ai+wi一定大于aj),若①式取的是aj+wj,则先买i的代价是wi+wj+aj,此时先买j的花i只可能是wj+ai+wi,（ai>aj,∴ai+wi>aj）,此时①一定小于②，所以无论怎样都是先买i更优

蒟蒻不会写代码只好用zay的了

#include <cstdio>
#include <vector>
#include <algorithm>

const int maxn = ;

int n;
int MU[maxn], ans[maxn];//MU就是点的权值
std::vector<int>son[maxn];//动态数组（省空间） 

void dfs(const int u);
bool cmp(const int &_a, const int &_b);

int main() {
  freopen("yin.in", "r", stdin);
  freopen("yin.out", "w", stdout);//这里写错了会被zay严厉批评的
  scanf("%d", &n);
  for (int i = , x; i <= n; ++i) {
    scanf("%d", &x);
    son[x].push_back(i);
  }
  for (int i = ; i <= n; ++i) {
    scanf("%d", MU + i);//这里是指针的表示方式，相当于scanf("%d",MU[i]);
  }
  dfs();
  for (int i = ; i < n; ++i) {
    printf("%d ", ans[i]);
  }
  printf("%d\n", ans[n]);
  return ;
}

void dfs(const int u) {
  for (auto v : son[u]) {//相当于遍历son[u]的所有子节点
    dfs(v);
  }
  std::sort(son[u].begin(), son[u].end(), cmp);//按照zay的式子进行排序
  int _ret = ;
  for (auto v : son[u]) {
    if (_ret >= ans[v]) {
      _ret -= ans[v]; // 更新之前的ret=ans[上一个v]-MU[上一个v],意思是如果上一个点的孩子节点收回的石头足够摆当前节点，就摆
    }
    else {
      ans[u] += ans[v] - _ret;//ans[上一个v]-ret=MU[上一个v]
      _ret = ans[v] - MU[v];
    }
  }
  ans[u] += std::max(, MU[u] - _ret);//由于是深搜，所以会先dfs到所有的叶节点，并且所有叶节点的ans=w叶节点
}

inline bool cmp(const int &_a, const int &_b) {
  return (ans[_a] - MU[_a]) > (ans[_b] - MU[_b]);//排序
}

T3:棠梨煎雪

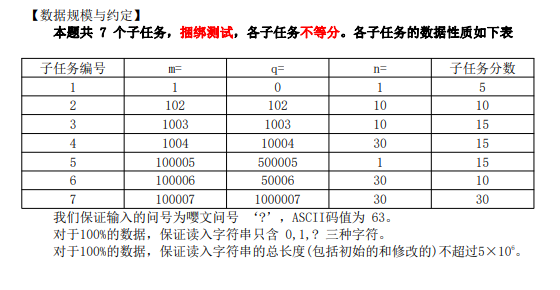
zayの题解：

数据小了依旧爆搜

我们来推理胡扯一下正解

状态压缩：

1.两个int状压

对于每个字符串第一个int f1（以下按照二进制记录），记录每一位是否必须是一个字符，第二个int记录必须是某个字符的位置的字符（0或1）

for example    01??00001?

f1=1100111110

f2=0100000010(在f1为0的对应位置f2可以是任意值，统一就好)

对于每一个字符串都如此记录，若判定两个字符串是否可以相同，我们就把记录下来的必须是0或1的部分摘出来，查看是否相同

a1:字符串a的f1,b1:字符串b1的f1,a2:字符串a的f2,b2:字符串b的f2

确定必须为某个字符的位置：a1&b1（为了和下一步的比较对应位置服务（zay题解写错了））

必须为0或1的位置的字符是否相同的判定：a2^b2（相同为0，不同为1）

两个合并 一下：(a1&b1)&(a2^b2)  为什么中间是& ?（zay的代码充满了指针和茫然）（请务必配合zay十分难懂的代码食用）

因为在必须是0或1的位置，字符相同，才可以判定是相同。

2.开个long long

一个long long 是64位，以每两位为一组，记录所比较的字符串该位置的情况

00:无解  ,  01：该位是0 , 10：该位是1 , 11：该位都是"?"

每进来一个新的字符串，进行&操作

看到这种有q次询问的，一般都是要用数据结构。

看到区间询问，单个字符串修改，我们可以想到一些和树有关的东西，例如线段树和树状数组

但这里我们用线段树

zay的代码太难懂了所以我也不知道他写了啥也不知道我自己加了啥注释

zay的标程

#include <cstdio>

template <typename T>
inline void qr(T &x) {//数字快读
  char ch = getchar(), lst = ' ';
  while ((ch > '') || (ch < '')) lst = ch, ch=getchar();
  while ((ch >= '') && (ch <= '')) x = (x << ) + (x << ) + (ch ^ ), ch = getchar();
  if (lst == '-') x = -x;
}

const int maxn = ;

int n, m, q;
char s[maxn][];

#ifdef ONLINE_JUDGE
int Ans;
#endif

struct Tree {
  Tree *ls, *rs;
  int l, r, x, y;
  bool leg;//是否合法 

  Tree() {
    ls = rs = NULL;
    l = r = x = y = ;
    leg = true;//我们先假设它是合法的
  }

  void pushup() {//目测是用来制造a1,a2,b1,b2用的
    if (!(this->ls->leg && this->rs->leg)) {
      this->leg = false;
    } else {
      if ((this->ls->x & this->rs->x) & (this->ls->y ^ this->rs->y)) {
        this->leg = false;
      } else {
        this->leg = true;
        this->x = this->ls->x | this->rs->x;
        this->y = this->ls->y | this->rs->y;
      }
    }
  }
};
Tree *rot;//线段树的根 

void ReadStr(char *p);//指针快读
void Update(const int x); //似乎没有用
void Query(const int l, const int r);
void update(Tree *const u, const int p);//修改
Tree query(Tree *u, const int l, const int r);//查询
void build(Tree *const u, const int l, const int r);//建树 

int main() {
  freopen("lin.in", "r", stdin);
  freopen("lin.out", "w", stdout);
  qr(n); qr(m); qr(q);
  for (int i = ; i <= m; ++i) {
    ReadStr(s[i] + );
  }
  build(rot = new Tree, , m);//建树
  int opt, l, r;
  while (q--) {
    opt = ; qr(opt);
    if (opt == ) {//查询
      l = r = ; qr(l); qr(r);
      Query(l, r);
    } else {
      l = ; qr(l);
      ReadStr(s[] + );
      Update(l);//修改第l个
    }
  }
#ifdef ONLINE_JUDGE//zay说这个没有什么用，可以去掉，但是这之间的东西都要删掉（删着删着就ce了）
  printf("%d\n", Ans);
#endif
  return ;
}

void ReadStr(char *p) {
  do *p = getchar(); while ((*p != '') && (*p != '') && (*p != '?'));
  do *(++p) = getchar(); while ((*p == '') || (*p == '') || (*p == '?'));
  *p = ;
}

void build(Tree *const u, const int l, const int r) {
  if ((u->l = l) == (u->r = r)) {
    for (int i = ; i <= n; ++i) {
      if (s[l][i] != '?') {
        u->x |=  << i;
        if (s[l][i] == '') {
          u->y |=  << i;
        }
      }
    }
  } else {
    int mid = (l + r) >> ;
    build(u->ls = new Tree, l, mid);
    build(u->rs = new Tree, mid + , r);
    u->pushup();
  }
}

Tree query(Tree *u, const int l, const int r) {
  if ((u->l > r) || (u->r < l)) return Tree();//如果当前区间完全不在查询区间内，就结束
  if ((u->l >= l) && (u->r <= r)) return *u;//完全在，就直接返回
  Tree _ret;
  auto ll = query(u->ls, l, r), rr = query(u->rs, l, r);//不然就递归来求
  _ret.ls = &ll; _ret.rs = &rr;
  _ret.pushup();
  return _ret;
}

void Query(const int l, const int r) {
  auto _ret = query(rot, l, r);
  if (!_ret.leg) {//如果不合法，就输出0
#ifndef ONLINE_JUDGE
    puts("");
#endif
  } else {
    int ans = ;
    for (int i = ; i <= n; ++i) if (!(_ret.x & ( << i))) {
      ans <<= ;
    }
#ifdef ONLINE_JUDGE
    Ans ^= ans;
#else
    printf("%d\n", ans);
#endif
  }
}

void update(Tree *u, const int p) {//修改第p个
  if (u->ls) {//找p在哪
    if (u->ls->r >= p) {//左子树的右端点如果比p大
      update(u->ls, p);
    } else {
      update(u->rs, p);
    }
    u->pushup();//把子节点的信息合并到父节点
  } else {
    *u = Tree();
    u->l = u->r = p;
    for (int i = ; i <= n; ++i) {
      if (s[][i] != '?') {
        u->x |=  << i;
        if (s[][i] == '') {
          u->y |=  << i;
        }
      }
    }
  }
}

void Update(const int x) {
  update(rot, x);//修改
}

接下来是water_lift很神奇但是似乎好懂那么一点的代码

#include <bits/stdc++.h>
using namespace std;
template <class T>
inline void read(T &num)
{
    bool flag = ;
    num = ;
    char c = getchar();
    while ((c < '' || c > '') && c != '-')
        c = getchar();
    if (c == '-')
    {
        flag = ;
        c = getchar();
    }
    num = c - '';
    c = getchar();
    while (c >= '' && c <= '')
        num = (num << ) + (num << ) + c - '', c = getchar();
    if (flag)
        num *= -;
}
template <class T>
inline void output(T num)
{
    if (num < )
    {
        putchar('-');
        num = -num;
    }
    if (num >= )
        output(num / );
    putchar(num %  + '');
}
template <class T>
inline void outln(T num)
{
    output(num);
    putchar('\n');
}
template <class T>
inline void outps(T num)
{
    output(num);
    putchar(' ');
}
const int N = , M = ;
int n, m, q;
struct segment
{
    char val[M];
    bool all1[M * ];
    bool all0[M * ];
    void init(int node, int nl, int nr)//这是个正常的线段树的板子（虽然位置好像不大正常）
    {
        if (nl < nr)
        {
            int mid = (nl + nr) >> ;
            init(node * , nl, mid);
            init(node *  + , mid + , nr);
            all1[node] = all1[node * ] & all1[node *  + ];
            all0[node] = all0[node * ] & all0[node *  + ];
        }
        else
        {
            if (val[nl] == '?')
                all1[node] = all0[node] = ;
            else
            {
                all1[node] = val[nl] == '';
                all0[node] = val[nl] == '';
            }
        }
    }
    void modify(int node, int nl, int nr, int x, char va)
    {
        if (val[x] == va)
            return;
        if (nl < nr)
        {
            int mid = (nl + nr) >> ;
            if (x <= mid)
            {
                modify(node * , nl, mid, x, va);
            }
            else
            {
                modify(node *  + , mid + , nr, x, va);
            }
            all1[node] = all1[node * ] & all1[node *  + ];
            all0[node] = all0[node * ] & all0[node *  + ];
        }
        else
        {
            if (va == '?')
                all1[node] = all0[node] = ;
            else
            {
                all1[node] = va == '';
                all0[node] = va == '';
            }
            val[x] = va;
        }
    }
    pair<bool, bool> query(int node, int nl, int nr, int l, int r)
    {
        if (l <= nl && r >= nr)
        {
            return make_pair(all1[node], all0[node]);
        }
        int mid = (nl + nr) >> ;
        bool a1 = true, a0 = true;
        if (l <= mid)
        {
            auto lo = query(node * , nl, mid, l, r);
            a1 &= lo.first;
            a0 &= lo.second;
        }
        if (r >= mid + )
        {
            auto lo = query(node *  + , mid + , nr, l, r);
            a1 &= lo.first;
            a0 &= lo.second;
        }
        return make_pair(a1, a0);
    }
    void dfs(int node, int nl, int nr)
    {
        if (nl < nr)
        {
            int mid = (nl + nr) >> ;
            dfs(node * , nl, mid);
            dfs(node *  + , mid + , nr);
        }
        outps(nl);
        outps(nr);
        outps(all1[node]);
        outln(all0[node]);
    }
} segs[N];
int main()
{
    freopen("lin.in", "r", stdin);
    freopen("lin.out", "w", stdout);
    read(n);
    read(m);
    read(q);
    char ch;
    for (int i = ; i <= m; i++)
    {
        for (int j = ; j <= n; j++)
        {
            do
            {
                ch = getchar();
            } while (ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t' || ch == '\0');
            segs[j].val[i] = ch;
        }
    }
    for (int i = ; i <= n; i++)
    {
        segs[i].init(, , m);
    }
    while (q--)
    {
        bool opt;
        read(opt);
        if (opt == )
        {
            int l, r;
            read(l);
            read(r);
            int ans = ;
            for (int i = ; i <= n; i++)
            {
                auto lo = segs[i].query(, , m, l, r);
                ans *= (lo.first + lo.second);
            }
            outln(ans);
        }
        else
        {
            int pos;
            read(pos);
            for (int i = ; i <= n; i++)
            {
                do
                {
                    ch = getchar();
                } while (ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t' || ch == '\0');
                segs[i].modify(, , m, pos, ch);
            }
        }
    }
}