C 数据结构堆

引言 - 数据结构堆

　　堆结构都多数人很耳熟, 从堆排序到优先级队列, 我们总会看见它的身影. 相关的资料太多了,

堆 - https://zh.wikipedia.org/wiki/%E5%A0%86%E7%A9%8D

无数的漂亮图片接二连三, 但目前没搜到一个工程中可以舒服用的代码库. 本文由此痛点而来. 写

一篇奇妙数据结构堆的工程代码. 追求愣头青的手热 ->---

对于 heap 接口思考, 我是这样设计

#ifndef _H_HEAP
#define _H_HEAP

//
// cmp_f - 比较行为 > 0 or = 0  or < 0
// : int add_cmp(const void * now, const void * node)
//
typedef int (* cmp_f)();

//
// node_f - 销毁行为
// : void list_die(void * node)
//
typedef void (* node_f)(void * node);

//
// head_t 堆的类型结构
//
typedef struct heap * heap_t;

//
// heap_create - 创建符合规则的堆
// fcmp     : 比较行为, 规则 fcmp() <= 0
// return   : 返回创建好的堆对象
//
extern heap_t heap_create(cmp_f fcmp);

//
// heap_delete - 销毁堆
// h        : 堆对象
// fdie     : 销毁行为, 默认 NULL
// return   : void
//
extern void heap_delete(heap_t h, node_f fdie);

//
// heap_insert - 堆插入数据
// h        : 堆对象
// node     : 操作对象
// return   : void
//
extern void heap_insert(heap_t h, void * node);

//
// heap_remove - 堆删除数据
// h        : 堆对象
// arg      : 操作参数
// fcmp     : 比较行为, 规则 fcmp() == 0
// return   : 找到的堆节点
//
extern void * heap_remove(heap_t h, void * arg, cmp_f fcmp);

//
// heap_top - 查看堆顶结点数据
// h        : 堆对象
// return   : 堆顶节点
//
extern void * heap_top(heap_t h);

//
// heap_top - 摘掉堆顶结点数据
// h        : 堆对象
// return   : 返回堆顶节点
//
extern void * heap_pop(heap_t h);

#endif//_H_HEAP

heap_t 是不完全类型实体指针, 其中 struct heap 是这样设计

#include "heap.h"
#include <stdlib.h>
#include <assert.h>

#define UINT_HEAP       (1<<5u)

struct heap {
    cmp_f   fcmp;       // 比较行为
    unsigned len;       // heap 长度
    unsigned cap;       // heap 容量
    void ** data;       // 数据节点数组
};

// heap_expand - 添加节点扩容
inline void heap_expand(struct heap * h) {
    if (h->len >= h->cap) {
        h->data = realloc(h->data, h->cap<<=);
        assert(h->data);
    }
}

从中可以看出当前堆结构是可以保存 void * 数据. 其中通过 heap::fcmp 比较行为来调整关系.

有了堆的数据结构定义, 那么堆的创建和销毁业务代码就被无脑的确定了 ~

//
// heap_create - 创建符合规则的堆
// fcmp     : 比较行为, 规则 fcmp() <= 0
// return   : 返回创建好的堆对象
//
inline heap_t
heap_create(cmp_f fcmp) {
    struct heap * h = malloc(sizeof(struct heap));
    assert(h && fcmp);
    h->fcmp = fcmp;
    h->len = ;
    h->cap = UINT_HEAP;
    h->data = malloc(sizeof(void *) * UINT_HEAP);
    assert(h->data && UINT_HEAP > );
    return h;
}

//
// heap_delete - 销毁堆
// h        : 堆对象
// fdie     : 销毁行为, 默认 NULL
// return   : void
//
void
heap_delete(heap_t h, node_f fdie) {
    if (NULL == h || h->data == NULL) return;
    if (fdie && h->len > )
        for (unsigned i = ; i < h->len; ++i)
            fdie(h->data[i]);
    free(h->data);
    h->data = NULL;
    h->len = ;
    free(h);
}

随后将迎接这个终结者堆的全貌. 此刻读者可以先喝口水 : )

前言 - 写一段终结代码

　　堆结构中最核心两处就是向下调整和向上调整过程代码

// down - 堆节点下沉, 从上到下沉一遍
static void down(cmp_f fcmp, void * data[], unsigned len, unsigned x) {
    void * m = data[x];
    for (unsigned i = x *  + ; i < len; i = x *  + ) {
        if (i +  < len && fcmp(data[i+], data[i]) < )
            ++i;
        if (fcmp(m, data[i]) <= )
            break;
        data[x] = data[i];
        x = i;
    }
    data[x] = m;
}

// up - 堆节点上浮, 从下到上浮一遍
static void up(cmp_f fcmp, void * node, void * data[], unsigned x) {
    while (x > ) {
        void * m = data[(x-)>>];
         if (fcmp(m, node) <= )
            break;
        data[x] = m;
        x = (x-)>>;
    }
    data[x] = node;
}

如何理解其中奥妙呢. 可以这么看, 索引 i 节点的左子树索引为 2i+1, 右子树树索引为 2i+2 = (2i+1)+1.

相反的索引为 i 节点的父亲节点就是 (i-1)/2 = (i-1)>>1. 这就是堆节点调整的无上奥妙.  随后的代码就

很轻松出手了

//
// heap_insert - 堆插入数据
// h        : 堆对象
// node     : 操作对象
// return   : void
//
inline void
heap_insert(heap_t h, void * node) {
    heap_expand(h);
    up(h->fcmp, node, h->data, h->len++);
}

//
// heap_top - 查看堆顶结点数据
// h        : 堆对象
// return   : 堆顶节点
//
inline void *
heap_top(heap_t h) {
    return h->len <=  ? NULL : *h->data;
}

//
// heap_top - 摘掉堆顶结点数据
// h        : 堆对象
// return   : 返回堆顶节点
//
inline void *
heap_pop(heap_t h) {
    void * node = heap_top(h);
    if (node && --h->len > ) {
        // 尾巴节点一定比小堆顶节点大, 那么要下沉
        h->data[] = h->data[h->len];
        down(h->fcmp, h->data, h->len, );
    }
    return node;
}

看完上面代码可以再回看下 down 和 up 代码布局. 是不是堆节点调整全部技巧已经了然于胸 ~

随后我们介绍堆删除任意节点大致算法思路

　　1' 循环遍历, 找到要删除节点

　　2' 如果删除后堆空, 或者删除的是最后节点, 那直接搞定

　　3' 最后节点复制到待删除节点位置处

　　4' 最后节点和待删除节点权值相等, 不调整节点关系

　　5' 最后节点比待删除节点权值大, 向下调整节点关系(基于小顶堆设计)

　　6' 最后节点比待删除节点权值小, 向上调整节点关系

从上可以看出堆删除节点算法复杂度是 O(n) + O(logn) = O(n). 请欣赏具体代码

//
// heap_remove - 堆删除数据
// h        : 堆对象
// arg      : 操作参数
// fcmp     : 比较行为, 规则 fcmp() == 0
// return   : 找到的堆节点
//
void *
heap_remove(heap_t h, void * arg, cmp_f fcmp) {
    if (h == NULL || h->len <= )
        return NULL;

    // 开始查找这个节点
    unsigned i = ;
    fcmp = fcmp ? fcmp : h->fcmp;
    do {
        void * node = h->data[i];
        if (fcmp(arg, node) == ) {
            if (--h->len >  && h->len != i) {
                // 尾巴节点和待删除节点比较
                int ret = h->fcmp(h->data[h->len], node);

                // 小顶堆, 新的值比老的值小, 那么上浮
                if (ret < )
                    up(h->fcmp, h->data[h->len], h->data, i);
                else if (ret > ) {
                    // 小顶堆, 新的值比老的值大, 那么下沉
                    h->data[i] = h->data[h->len];
                    down(h->fcmp, h->data, h->len, i);
                }
            }

            return node;
        }
    } while (++i < h->len);

    return NULL;
}

到这堆数据结构基本代码都已经搞定. 开始写写测试用例跑跑

#include "heap.h"
#include <stdio.h>

struct node {
    int value;
};

static inline int node_cmp(const struct node * l, const struct node * r) {
    return l->value - r->value;
}

static void heap_print(heap_t h) {
    struct heap {
        cmp_f   fcmp;       // 比较行为
        unsigned len;       // heap 长度
        unsigned cap;       // heap 容量
        void ** data;       // 数据节点数组
    } * x = (struct heap *)h;

    // 数据打印for (unsigned i = ; i < x->len; ++i) {
        struct node * node = x->data[i];
        printf("%d ", node->value);
    }
    putchar('\n');
}

int main() {
    heap_t h = heap_create(node_cmp);
    struct node a[] = { {  }, {  }, {  }, {  }, {  }, {  }, {  }, { } };
    for (int i = ; i < sizeof a / sizeof *a; ++i)
        heap_insert(h, a + i);

    heap_print(h);

    // 数据打印
    struct node * node;
    while ((node = heap_pop(h))) {
        printf("%d ", node->value);
    }
    putchar('\n');

    // 重新插入数据
    for (int i = ; i < sizeof a / sizeof *a; ++i)
        heap_insert(h, a + i);

    // 删除操作 - 下沉
    heap_remove(h, &(struct node){  }, NULL);
    heap_print(h);

    // 插入操作
    heap_insert(h, &(struct node){  });
    heap_print(h);

    // 删除操作 - 上浮
    heap_remove(h, &(struct node){  }, NULL);
    heap_print(h);

    heap_delete(h, NULL);
    return ;
}

最终运行结果如下

　

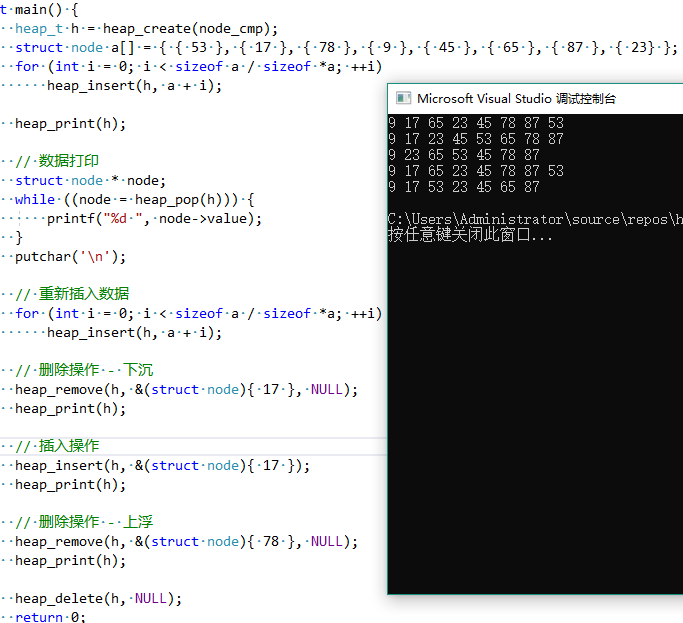
后续堆相关代码变化, 可以参照  heap - https://github.com/wangzhione/structc/blob/master/structc/struct/heap.c

说到引用 github 想起一个 git 好用配置安利给大家 ~ 从此 git ll 就活了.

git config --global color.diff auto
git config --global color.status auto
git config --global color.branch auto
git config --global color.interactive auto
git config --global alias.ll "log --graph --all --pretty=format:'%Cred%h %Creset -%C(yellow)%d%Creset %s %Cgreen(%cr) %C(bold blue)<%an>%Creset' --abbrev-commit --date=relative"

奇妙数据结构堆, 终结在这里, 后面内容可以忽略. 期待下次再扯了 ~

正文 - 顺带赠送个点心

　　其实到这本不该再说什么. 单纯看上面就足够了. 但不知道有没有朋友觉得你总是说 C 数据结构. 效

果好吗? 对技术提升效果明显吗? 这里不妨利用我们对 C 理解, 来分析一个业务代码. 感受下一通百通.

我试着用 Go 中数据结构源码举例子. 重点看下 Go 源码包中 "container/list" 链表用法(比较简单)

package main

import (
	"container/list"
	"fmt"
)

func main() {
	// 构造链表对象
	pers := list.New()

	// Persion 普通人对象
	type Persion struct {
		Name string
		Age  int
	}

	// 链表对象数据填充
	pers.PushBack(&Persion{"wang", 27})
	pers.PushFront(&Persion{"zhi", 27})

	// 开始遍历处理
	for e := pers.Front(); e != nil; e = e.Next() {
		per, ok := e.Value.(*Persion)
		if !ok {
			panic(fmt.Sprint("Persion List faild", e.Value))
		}
		fmt.Println(per)
	}

	for e := pers.Front(); e != nil; {
		next := e.Next()
		pers.Remove(e)
		e = next
	}
	fmt.Println(pers.Len())
}

运行结果是

$ go run list-demo.go
&{zhi }
&{wang }

通过上面演示 Demo, 大致知道了 list 包用法. 随后开始着手解析 "container/list" 源码

// Copyright 2009 The Go Authors. All rights reserved.
// Use of this source code is governed by a BSD-style
// license that can be found in the LICENSE file.

// Package list implements a doubly linked list.
//
// To iterate over a list (where l is a *List):
//	for e := l.Front(); e != nil; e = e.Next() {
//		// do something with e.Value
//	}
//
package list

// Element is an element of a linked list.
type Element struct {
	// Next and previous pointers in the doubly-linked list of elements.
	// To simplify the implementation, internally a list l is implemented
	// as a ring, such that &l.root is both the next element of the last
	// list element (l.Back()) and the previous element of the first list
	// element (l.Front()).
	next, prev *Element

	// The list to which this element belongs.
	list *List

	// The value stored with this element.
	Value interface{}
}

// Next returns the next list element or nil.
func (e *Element) Next() *Element {
	if p := e.next; e.list != nil && p != &e.list.root {
		return p
	}
	return nil
}

// Prev returns the previous list element or nil.
func (e *Element) Prev() *Element {
	if p := e.prev; e.list != nil && p != &e.list.root {
		return p
	}
	return nil
}

// List represents a doubly linked list.
// The zero value for List is an empty list ready to use.
type List struct {
	root Element // sentinel list element, only &root, root.prev, and root.next are used
	len  int     // current list length excluding (this) sentinel element
}

// Init initializes or clears list l.
func (l *List) Init() *List {
	l.root.next = &l.root
	l.root.prev = &l.root
	l.len = 0
	return l
}

// New returns an initialized list.
func New() *List { return new(List).Init() }

// Len returns the number of elements of list l.
// The complexity is O(1).
func (l *List) Len() int { return l.len }

// Front returns the first element of list l or nil if the list is empty.
func (l *List) Front() *Element {
	if l.len == 0 {
		return nil
	}
	return l.root.next
}

// Back returns the last element of list l or nil if the list is empty.
func (l *List) Back() *Element {
	if l.len == 0 {
		return nil
	}
	return l.root.prev
}

// lazyInit lazily initializes a zero List value.
func (l *List) lazyInit() {
	if l.root.next == nil {
		l.Init()
	}
}

// insert inserts e after at, increments l.len, and returns e.
func (l *List) insert(e, at *Element) *Element {
	n := at.next
	at.next = e
	e.prev = at
	e.next = n
	n.prev = e
	e.list = l
	l.len++
	return e
}

// insertValue is a convenience wrapper for insert(&Element{Value: v}, at).
func (l *List) insertValue(v interface{}, at *Element) *Element {
	return l.insert(&Element{Value: v}, at)
}

// remove removes e from its list, decrements l.len, and returns e.
func (l *List) remove(e *Element) *Element {
	e.prev.next = e.next
	e.next.prev = e.prev
	e.next = nil // avoid memory leaks
	e.prev = nil // avoid memory leaks
	e.list = nil
	l.len--
	return e
}

// Remove removes e from l if e is an element of list l.
// It returns the element value e.Value.
// The element must not be nil.
func (l *List) Remove(e *Element) interface{} {
	if e.list == l {
		// if e.list == l, l must have been initialized when e was inserted
		// in l or l == nil (e is a zero Element) and l.remove will crash
		l.remove(e)
	}
	return e.Value
}

// PushFront inserts a new element e with value v at the front of list l and returns e.
func (l *List) PushFront(v interface{}) *Element {
	l.lazyInit()
	return l.insertValue(v, &l.root)
}

// PushBack inserts a new element e with value v at the back of list l and returns e.
func (l *List) PushBack(v interface{}) *Element {
	l.lazyInit()
	return l.insertValue(v, l.root.prev)
}

// InsertBefore inserts a new element e with value v immediately before mark and returns e.
// If mark is not an element of l, the list is not modified.
// The mark must not be nil.
func (l *List) InsertBefore(v interface{}, mark *Element) *Element {
	if mark.list != l {
		return nil
	}
	// see comment in List.Remove about initialization of l
	return l.insertValue(v, mark.prev)
}

// InsertAfter inserts a new element e with value v immediately after mark and returns e.
// If mark is not an element of l, the list is not modified.
// The mark must not be nil.
func (l *List) InsertAfter(v interface{}, mark *Element) *Element {
	if mark.list != l {
		return nil
	}
	// see comment in List.Remove about initialization of l
	return l.insertValue(v, mark)
}

// MoveToFront moves element e to the front of list l.
// If e is not an element of l, the list is not modified.
// The element must not be nil.
func (l *List) MoveToFront(e *Element) {
	if e.list != l || l.root.next == e {
		return
	}
	// see comment in List.Remove about initialization of l
	l.insert(l.remove(e), &l.root)
}

// MoveToBack moves element e to the back of list l.
// If e is not an element of l, the list is not modified.
// The element must not be nil.
func (l *List) MoveToBack(e *Element) {
	if e.list != l || l.root.prev == e {
		return
	}
	// see comment in List.Remove about initialization of l
	l.insert(l.remove(e), l.root.prev)
}

// MoveBefore moves element e to its new position before mark.
// If e or mark is not an element of l, or e == mark, the list is not modified.
// The element and mark must not be nil.
func (l *List) MoveBefore(e, mark *Element) {
	if e.list != l || e == mark || mark.list != l {
		return
	}
	l.insert(l.remove(e), mark.prev)
}

// MoveAfter moves element e to its new position after mark.
// If e or mark is not an element of l, or e == mark, the list is not modified.
// The element and mark must not be nil.
func (l *List) MoveAfter(e, mark *Element) {
	if e.list != l || e == mark || mark.list != l {
		return
	}
	l.insert(l.remove(e), mark)
}

// PushBackList inserts a copy of an other list at the back of list l.
// The lists l and other may be the same. They must not be nil.
func (l *List) PushBackList(other *List) {
	l.lazyInit()
	for i, e := other.Len(), other.Front(); i > 0; i, e = i-1, e.Next() {
		l.insertValue(e.Value, l.root.prev)
	}
}

// PushFrontList inserts a copy of an other list at the front of list l.
// The lists l and other may be the same. They must not be nil.
func (l *List) PushFrontList(other *List) {
	l.lazyInit()
	for i, e := other.Len(), other.Back(); i > 0; i, e = i-1, e.Prev() {
		l.insertValue(e.Value, &l.root)
	}
}

list 包中最核心的数据结构无外乎 Element 和 List 互相引用的结构

// Element is an element of a linked list.
type Element struct {
	// Next and previous pointers in the doubly-linked list of elements.
	// To simplify the implementation, internally a list l is implemented
	// as a ring, such that &l.root is both the next element of the last
	// list element (l.Back()) and the previous element of the first list
	// element (l.Front()).
	next, prev *Element

	// The list to which this element belongs.
	list *List

	// The value stored with this element.
	Value interface{}
}

// Next returns the next list element or nil.
func (e *Element) Next() *Element {
	if p := e.next; e.list != nil && p != &e.list.root {
		return p
	}
	return nil
}

// Prev returns the previous list element or nil.
func (e *Element) Prev() *Element {
	if p := e.prev; e.list != nil && p != &e.list.root {
		return p
	}
	return nil
}

// List represents a doubly linked list.
// The zero value for List is an empty list ready to use.
type List struct {
	root Element // sentinel list element, only &root, root.prev, and root.next are used
	len  int     // current list length excluding (this) sentinel element
}

它是一个特殊循环双向链表. 特殊在 Element::list 指向头节点.

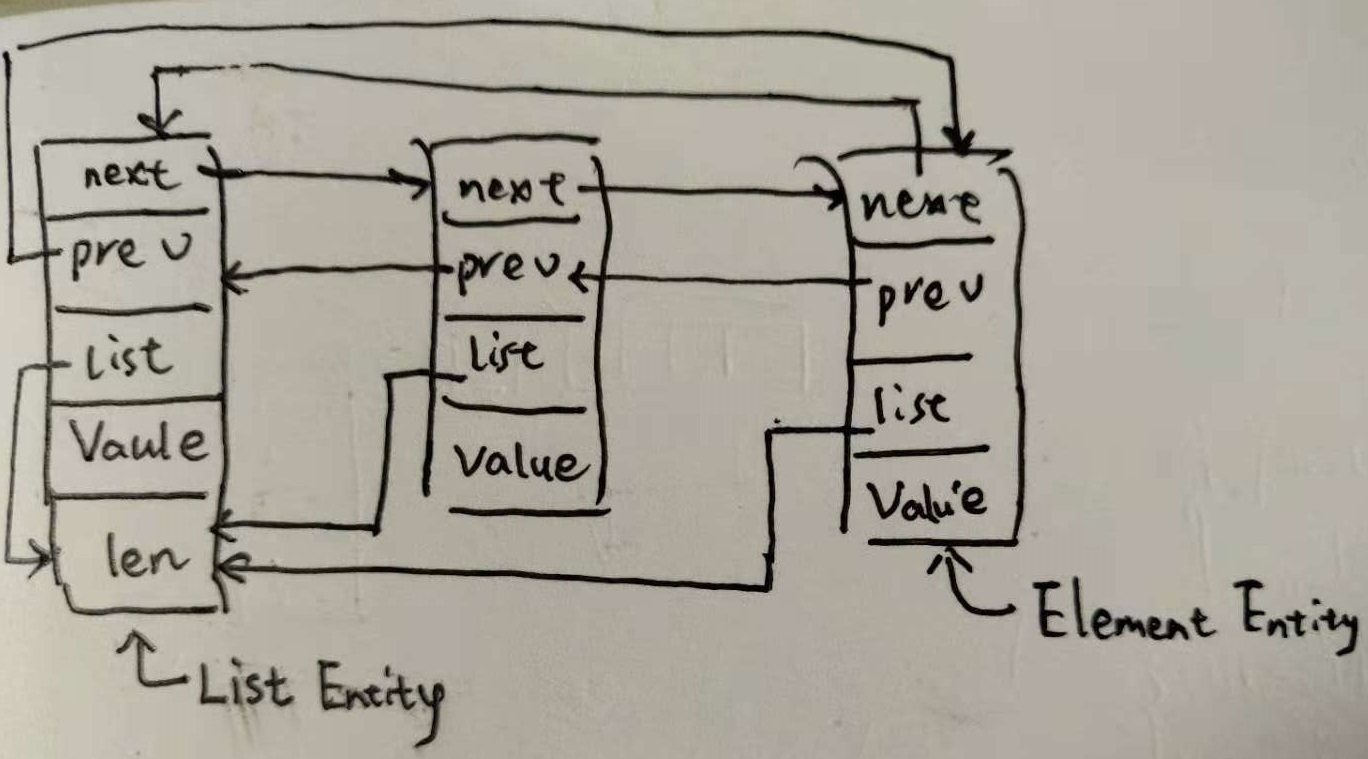
随着我们对 list 内存布局理解后, 后面的业务代码实现起来就很一般了. 例如这里

// PushBackList inserts a copy of an other list at the back of list l.
// The lists l and other may be the same. They must not be nil.
func (l *List) PushBackList(other *List) {
	l.lazyInit()
	for i, e := other.Len(), other.Front(); i > 0; i, e = i-1, e.Next() {
		l.insertValue(e.Value, l.root.prev)
	}
}

其实可以实现的更贴合 list 库总体的风格, 性能还更好

// PushBackList inserts a copy of an other list at the back of list l.
// The lists l and other may be the same. They must not be nil.
func (l *List) PushBackList(other *List) {
	l.lazyInit()
	for e := other.Front(); e != nil; e = e.Next() {
		l.insertValue(e.Value, l.root.prev)
	}
}

是不是发现上层代码理解起来心智负担不大. 不过 go 中 slice list map 都不是线程安全的.

特殊场景需要自行加锁. 这里不过多扯. 以后有机会会详细分析 Go 中锁源码实现. 最后通过

上面 list 包真实现一个 LRU Cache

package cache

import (
    "container/list"
    "sync"
)

// entry 存储的实体
type entry struct {
    key, val interface{}
}

// Cache 缓存结构
type Cache struct {
    // m 保证 LRU Cache 访问线程安全
    m sync.Mutex

    // max 标识缓存容量的最大值, 0 标识无限缓存
    max uint

    // list 是 entry 循环双向链表
    list *list.List

    // pond entry 缓存池子 key -> entry
    pond map[interface{}]*list.Element
}

// New 构建 LRU Cache 缓存结构
func New(max uint) *Cache {
    return &Cache{
        max:  max,
        list: list.New(),
        pond: make(map[interface{}]*list.Element),
    }
}

// Set 设置缓存
func (c *Cache) Set(key, val interface{}) {
    c.m.Lock()
    defer c.m.Unlock()

    element, ok := c.pond[key]
    if ok {
        // set key nil 进入删除逻辑
        if val == nil {
            delete(c.pond, key)
            c.list.Remove(element)
            return
        }

        // 重新设置 value 数据
        (element.Value.(*entry)).val = val
        // set key nil exists 进入 update 逻辑
        c.list.MoveToFront(element)
        return
    }

    if val == nil {
        return
    }

    // 首次添加
    c.pond[key] = c.list.PushFront(&entry{key, val})

    // 数据过多, 删除尾巴数据
    if uint(c.list.Len()) > c.max && c.max !=  {
        delete(c.pond, (c.list.Remove(c.list.Back()).(*entry)).key)
    }
}

// Get 获取缓存
func (c *Cache) Get(key interface{}) (val interface{}, ok bool) {
    c.m.Lock()
    defer c.m.Unlock()

    if element, ok := c.pond[key]; ok {
        // 获取指定缓存值
        val, ok = (element.Value.(*entry)).val, true
        // 调整缓存热点
        c.list.MoveToFront(element)
    }
    return
}

用起来很容易

	c := cache.New(1)
	c.Set("123", "123")
	c.Set("234", "234")
	fmt.Println(c.Get("123"))
	fmt.Println(c.Get("234"))

是不是离开了 C, 整个世界也很简单. 没啥设计模式, 有的是性能还可以, 也能用. 希望能帮到有心人 ~

也可以看看 Go 标准库中关于 LRU 局部源码, 也有些参照意义 (ˇˍˇ) ～

package transport

import "container/list"

//
// $(GOPATH)/src/net/http/transport.go
//

type persistConn struct {
    // ...
}

type connLRU struct {
    ll *list.List // list.Element.Value type is of *persistConn
    m  map[*persistConn]*list.Element
}

// add adds pc to the head of the linked list.
func (cl *connLRU) add(pc *persistConn) {
    if cl.ll == nil {
        cl.ll = list.New()
        cl.m = make(map[*persistConn]*list.Element)
    }
    ele := cl.ll.PushFront(pc)
    if _, ok := cl.m[pc]; ok {
        panic("persistConn was already in LRU")
    }
    cl.m[pc] = ele
}

func (cl *connLRU) removeOldest() *persistConn {
    ele := cl.ll.Back()
    pc := ele.Value.(*persistConn)
    cl.ll.Remove(ele)
    delete(cl.m, pc)
    return pc
}

// remove removes pc frpm cl.
func (cl *connLRU) remove(pc *persistConn) {
    if ele, ok := cl.m[pc]; ok {
        cl.ll.Remove(ele)
        delete(cl.m, pc)
    }
}

// len returns the number of items in the cache.
func (cl *connLRU) len() int {
    return len(cl.m)
}

后记 - 那个打开的大门

你曾是少年 - https://music.163.com/#/song?id=426027293

每个男人心里都有一块净土, 只不过生活所逼硬生生的, 藏在心底最深处 . ... ..