1997: [Hnoi2010]Planar

1997: [Hnoi2010]Planar

链接

分析：

　　首先在给定的那个环上考虑进行操作，如果环内有有两条边相交，那么可以把其中的一条放到环的外面去。所以转换为2-sat问题。

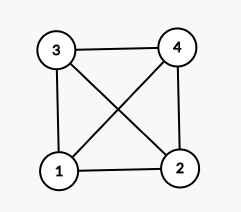
像这样，由于1-4和2-3在环内相交了，所以可以把1-4放到环外，就变成了下图。

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<cctype>
#include<set>
#include<queue>
#include<vector>
#include<map>
using namespace std;
typedef long long LL;

inline int read() {
    int x=,f=;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-;
    for(;isdigit(ch);ch=getchar())x=x*+ch-'';return x*f;
}

const int N = ;
struct Edge{ int to, nxt; } e[];
int head[N], dfn[N], low[N], bel[N], sk[N], c[N], pos[N], top, Index, tot, En;
bool vis[N];
pair<int,int> g[];

inline void add_edge(int u,int v) {
    ++En; e[En].to = v, e[En].nxt = head[u]; head[u] = En;
}
void tarjan(int u) {
    low[u] = dfn[u] = ++Index;
    sk[++top] = u; vis[u] = ;
    for (int i = head[u]; i; i = e[i].nxt) {
        int v = e[i].to;
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        if (vis[v]) low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++tot;
        do {
            vis[sk[top]] = ;
            bel[sk[top]] = tot;
            top --;
        } while (sk[top + ] != u);
    }
}
bool judge(int a,int b,int c,int d) {
    if (b > c && b < d && a < c) return ;
    if (a > c && a < d && b > d) return ;
    return ;
}
void solve() {
    int n = read(), m = read(), cnt = ;
    for (int i = ; i <= m; ++i)
        g[i].first = read(), g[i].second = read();
    for (int i = ; i <= n; ++i) c[i] = read();
    if (m >  * n - ) { puts("NO"); return ; }
    for (int i = ; i <= n; ++i) pos[c[i]] = i;
    for (int i = ; i <= m; ++i) {
        g[i].first = pos[g[i].first], g[i].second = pos[g[i].second];
        if (g[i].first > g[i].second) swap(g[i].first, g[i].second);
        if (g[i].second - g[i].first ==  || (g[i].first ==  && g[i].second == n)) continue;
        g[++cnt] = g[i];
    }
    m = cnt;
    for (int i = ; i <= m; ++i)
        for (int j = i + ; j <= m; ++j) {
            if (judge(g[i].first, g[i].second, g[j].first, g[j].second)) {
                add_edge(i, j + m);
                add_edge(i + m, j);
                add_edge(j, i + m);
                add_edge(j + m, i);
            }
        }
    for (int i = ; i <= m + m; ++i) if (!dfn[i]) tarjan(i);
    bool flag = ;
    for (int i = ; i <= m; ++i) if (bel[i] == bel[i + m]) flag = ;
    puts(flag ? "YES" : "NO");
    top = Index = En = tot = ;
    for (int i = ; i <= m + m; ++i)
        head[i] = dfn[i] = low[i] = bel[i] = ;
}
int main() {
    for (int T = read(); T--; ) solve();
    return ;
}