【刷题】HDU 3435 A new Graph Game

Problem Description

An undirected graph is a graph in which the nodes are connected by undirected arcs. An undirected arc is an edge that has no arrow. Both ends of an undirected arc are equivalent--there is no head or tail. Therefore, we represent an edge in an undirected graph as a set rather than an ordered pair.

Now given an undirected graph, you could delete any number of edges as you wish. Then you will get one or more connected sub graph from the original one (Any of them should have more than one vertex).

You goal is to make all the connected sub graphs exist the Hamiltonian circuit after the delete operation. What’s more, you want to know the minimum sum of all the weight of the edges on the “Hamiltonian circuit” of all the connected sub graphs (Only one “Hamiltonian circuit” will be calculated in one connected sub graph! That is to say if there exist more than one “Hamiltonian circuit” in one connected sub graph, you could only choose the one in which the sum of weight of these edges is minimum).

For example, we may get two possible sums:

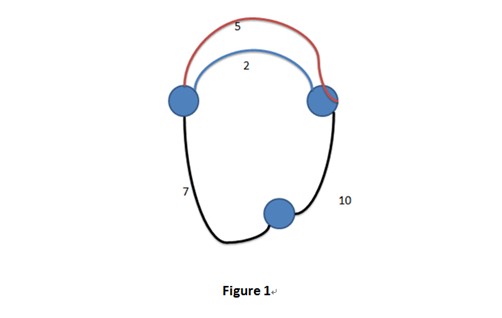
(1) 7 + 10 + 5 = 22

(2) 7 + 10 + 2 = 19

(There are two “Hamiltonian circuit” in this graph!)

Input

In the first line there is an integer T, indicates the number of test cases. (T <= 20)

In each case, the first line contains two integers n and m, indicates the number of vertices and the number of edges. (1 <= n <=1000, 0 <= m <= 10000)

Then m lines, each line contains three integers a,b,c ,indicates that there is one edge between a and b, and the weight of it is c . (1 <= a,b <= n, a is not equal to b in any way, 1 <= c <= 10000)

Output

Output “Case %d: “first where d is the case number counted from one. Then output “NO” if there is no way to get some connected sub graphs that any of them exists the Hamiltonian circuit after the delete operation. Otherwise, output the minimum sum of weight you may get if you delete the edges in the optimal strategy.

Sample Input

3

3 4

1 2 5

2 1 2

2 3 10

3 1 7

3 2

1 2 3

1 2 4

2 2

1 2 3

1 2 4

Sample Output

Case 1: 19

Case 2: NO

Case 3: 6

Hint

In Case 1:

You could delete edge between 1 and 2 whose weight is 5.

In Case 2:

It’s impossible to get some connected sub graphs that any of them exists the Hamiltonian circuit after the delete operation.

Description(CHN)

有n个点和m条边，你可以删去任意条边，使得所有点在一个哈密顿路径上，路径的权值得最小。

Solution

实际上就是找有向图最小权环覆盖

经典套路，一个点拆成入点和出点，如果有 \(u\) 到 \(v\) 的边，那么将 \(u\) 的出点连向 \(v\) 的入点

那么变成了一个二分图，这个二分图的一个完美匹配就是原图中的一个环覆盖

如果边有权，要求最小或最大，其实就是二分图最大权匹配

跑费用流即可

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=1000+10,MAXM=10000+10,inf=2147483647;
int T,tn,n,m,e=1,answas,beg[MAXN<<1],nex[MAXM<<3],to[MAXM<<3],cap[MAXM<<3],cur[MAXN<<1],p[MAXN<<1],s,t,vis[MAXN<<1],clk,G[MAXN][MAXN];
ll was[MAXM<<2],level[MAXN<<2];
std::queue<int> q;
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void insert(int x,int y,int z,int w)
{
	to[++e]=y;
	nex[e]=beg[x];
	beg[x]=e;
	cap[e]=z;
	was[e]=w;
	to[++e]=x;
	nex[e]=beg[y];
	beg[y]=e;
	cap[e]=0;
	was[e]=-w;
}
inline bool bfs()
{
	for(register int i=1;i<=t;++i)level[i]=inf;
	level[s]=0;
	p[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		p[x]=0;
		for(register int i=beg[x];i;i=nex[i])
			if(cap[i]&&level[to[i]]>level[x]+was[i])
			{
				level[to[i]]=level[x]+was[i];
				if(!p[to[i]])p[to[i]]=1,q.push(to[i]);
			}
	}
	return level[t]!=inf;
}
inline int dfs(int x,int maxflow)
{
	if(x==t||!maxflow)return maxflow;
	int res=0;
	vis[x]=clk;
	for(register int &i=cur[x];i;i=nex[i])
		if((vis[x]^vis[to[i]])&&cap[i]&&level[to[i]]==(level[x]+was[i]))
		{
			int f=dfs(to[i],min(maxflow,cap[i]));
			res+=f;
			cap[i]-=f;
			cap[i^1]+=f;
			answas+=f*was[i];
			maxflow-=f;
			if(!maxflow)break;
		}
	vis[x]=0;
	return res;
}
inline int MCMF()
{
	int res=0;
	while(bfs())clk++,memcpy(cur,beg,sizeof(cur)),res+=dfs(s,inf);
	return res;
}
int main()
{
	read(T);
	while(T--)
	{
		printf("Case %d: ",++tn);
		e=1;memset(beg,0,sizeof(beg));clk=0;
		answas=0;
		read(n);read(m);
		for(register int i=1;i<=n;++i)
			for(register int j=1;j<=n;++j)G[i][j]=inf;
		for(register int i=1;i<=m;++i)
		{
			int u,v,k;read(u);read(v);read(k);
			chkmin(G[u][v],k),chkmin(G[v][u],k);
		}
		for(register int i=1;i<=n;++i)
			for(register int j=1;j<=n;++j)
				if(G[i][j]!=inf)insert(j,i+n,1,G[i][j]);
		s=n+n+1,t=s+1;
		for(register int i=1;i<=n;++i)insert(s,i,1,0),insert(i+n,t,1,0);
		if(MCMF()!=n)puts("NO");
		else write(answas,'\n');
	}
	return 0;
}