二叉查找树(BST)的实现

一、二叉树介绍

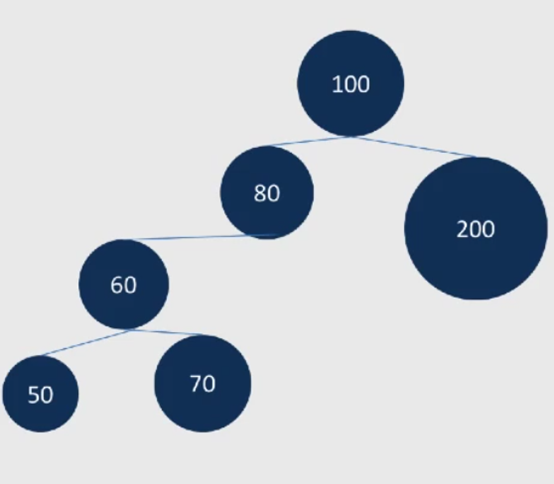
　　二叉查找树（Binary Search Tree，BST），又称二叉排序树，也称二叉搜索树，它或者是一颗空树，或者具有如下性质的树：若它的左子树不为空，则左子树上所有节点的值都小于根节点的值；若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。它的左右子树也分别为二叉查找树。

　　结论：中序遍历一颗二叉查找树可以得到一个按关键字递增的有序序列。简单来说，比根小的往左边放  比根大的往右边放。

　　　　

二、代码实现

　　1、BST结点类：

 public class BSTNode<K, V> {
     public K key;
     public V value;
     public BSTNode<K, V> left;
     public BSTNode<K, V> right;
     public BSTNode<K, V> parent;
     public boolean isLeftChild;
     public int height;
     public int num;
     public boolean isRed = true;  // 后面才学习的红黑树

     public BSTNode() {
     }

     public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right, BSTNode<K, V> parent) {
         super();
         this.key = key;
         this.value = value;
         this.left = left;
         this.right = right;
         this.parent = parent;
     }

     public boolean isLeft() {
         return isLeftChild;
     }

     public boolean isRight() {
         return !isLeftChild;
     }

     @Override
     public String toString() {
         return (isRed ? "红色" : "黑色") + " [" + key + "]<-" + (parent == null ? "" : parent.key);
     }
 }

　　2、BST接口：

 import java.util.List;
 import java.util.function.Consumer;

 public interface IBinarySearchTree<K, V> {
     /**
      * 新增节点
      * @param k 关键字
      * @param v 值
      */
     BSTNode<K, V> insert(K k, V v);

     /**
      * 中序遍历
      * @param con 处理中序遍历的每个元素的函数
      */
     void inorder(Consumer<K> con);

     /**
      * 查找元素
      * @param key
      * @return
      */
     V lookupValue(K key);

     /**
      * 获取最小关键字
      * @return
      */
     K min();

     /**
      * 获取最大关键字
      * @return
      */
     K max();

     /**
      * 移除关键字对应的节点
      * @param key
      */
     void remove(K key);

     /**
      * x的后继——比x大的第一个元素 1、是其右子树的最小值
      * 2、没有右子树，则向上追溯，直到某个祖先节点是左孩子，返回这个祖先节点的父节点，它就是x的后继
      *
      * @param x
      * @return
      */
     K successor(K x);

     /**
      * 前驱
      * @param x 关键字
      * @return
      */
     K predecessor(K x);

     boolean isBalance();

     /**
      * 返回节点数
      * @return
      */
     int getSize();

     /**
      * 高度
      * @return
      */
     int getHeight();

     List<List<BSTNode<K, V>>> levelOrder();
 }

　  3、BST实现：

 import java.util.ArrayList;
 import java.util.Comparator;
 import java.util.LinkedList;
 import java.util.List;
 import java.util.Queue;
 import java.util.Stack;
 import java.util.function.Consumer;

 /**
  * 二叉搜索树
  *
  */
 public class BinarySearchTree<K, V> implements IBinarySearchTree<K, V> {
   /**
    * 根节点
    */
   protected BSTNode root;
   /**
    * 元素个数
    */
   protected int size;
   private Comparator comparator;

   public BinarySearchTree() {
   }

   public BinarySearchTree(Comparator comparator) {
     this.comparator = comparator;
   }

   // parent curr 双指针
   @Override
   public BSTNode<K, V> insert(K key, V value) {
     if (!(key instanceof Comparable)) {
       throw new ClassCastException();
     }

     BSTNode<K, V> parent = null;
     BSTNode<K, V> curr = root;
     while (curr != null) {
       parent = curr;
       if (compare(key, curr.key) < 0) {
         curr = curr.left;
       } else if (compare(key, curr.key) > 0) {
         curr = curr.right;
       } else {
         curr.value = value;
         return curr;
       }
     }
     curr = new BSTNode(key, value, null, null, null);
     //link current to parent
     curr.parent = parent;
     if (parent == null) {
       root = curr;
     } else if (compare(key, parent.key) < 0) {
       parent.left = curr;
       curr.isLeftChild = true;
     } else {
       parent.right = curr;
       curr.isLeftChild = false;
     }

     size++;
     updateHeight(curr);
     return curr;
   }

   private void updateHeight(BSTNode<K, V> curr) {
     if (curr.parent == null) return;//util root

     BSTNode<K, V> p = curr.parent;
     if (p.height == curr.height) {
       p.height++;
       updateHeight(p);//递归
     }
   }

   @SuppressWarnings({"unchecked", "rawtypes"})
   private int compare(K key1, K key2) {
     if (null == comparator) {
       return ((Comparable) key1).compareTo((Comparable) key2);
     } else {
       return comparator.compare(key1, key2);
     }
   }

   /**
    * 中序遍历
    * @param con 处理中序遍历的每个元素的函数
    */
   @Override
   public void inorder(Consumer<K> con) {
     if (root != null)
       // inorder2(root, con);
       inorder(root, con);
   }

   /* 递归形式 */
   private void inorder(BSTNode<K, V> p, Consumer<K> con) {
     if (p != null) {
       inorder(p.left, con);
       con.accept(p.key);
       inorder(p.right, con);
     }
   }

   /*迭代形式*/
   private void inorder2(BSTNode<K, V> p, Consumer<K> con) {
     Stack<BSTNode<K, V>> stack = new Stack<>();
     BSTNode<K, V> curr = p;
     //curr不为空或者栈不为空，都可以继续处理
     while (curr != null || !stack.isEmpty()) {//没有生产也没有消费，就退出循环了
       //沿左支线一撸到底，全部入栈
       while (curr != null) {
         stack.push(curr);
         curr = curr.left;
       }
       //处理栈顶
       if (!stack.isEmpty()) {
         BSTNode<K, V> pop = stack.pop();
         con.accept(pop.key);
         //  curr指向pop的右子树，继续外层循环
         curr = pop.right;//有可能为空，为空，只消费栈中内容，不为空，就要向栈中生产若干内容
       }
     }
   }

   // 二叉查找树查找之所以快 每次丢弃一半  lgn
   @Override
   public V lookupValue(K key) {
     BSTNode<K, V> lookupNode = lookupNode(key);
     return lookupNode == null ? null : lookupNode.value;
   }

   protected BSTNode<K, V> lookupNode(K key) {
     BSTNode<K, V> p = root;
     //只要p不为空，并且没找到
     while (p != null && compare(key, p.key) != 0) {
       if (compare(key, p.key) < 0)
         p = p.left;
       else
         p = p.right;
     }
     return p;
   }

   // 最左边的结点
   @Override
   public K min() {
     return minNode(root).key;
   }

   protected BSTNode<K, V> minNode(BSTNode p) {
     while (p.left != null) {
       p = p.left;
     }
     return p;
   }

   // 最右边的结点
   @Override
   public K max() {
     return maxNode(root).key;
   }

   protected BSTNode<K, V> maxNode(BSTNode p) {
     while (p.right != null) {
       p = p.right;
     }
     return p;
   }

   /*右单旋
   *   p
   *   q
   *   */
   protected void rightRotate(BSTNode p, BSTNode q) {
     boolean pIsLeft = p.isLeft();
     BSTNode pp = p.parent;

     BSTNode x = q.right;
     p.left = x;
     if (x != null) {
       x.parent = p;
       x.isLeftChild = true;
     }
     q.right = p;
     p.parent = q;
     p.isLeftChild = false;

     //设定p和gg的关系
     q.parent = pp;
     if (pp == null) {
       root = q;
       return;
     }
     if (pIsLeft) {
       pp.left = q;
       q.isLeftChild = true;
     } else {
       pp.right = q;
       q.isLeftChild = false;
     }
   }

   /*左单旋*/
   protected void leftRotate(BSTNode p, BSTNode q) {
     boolean pIsLeft = p.isLeft();
     BSTNode pp = p.parent;
     //p和q的左子——B的关系
     BSTNode B = q.left;
     p.right = B;
     if (B != null) {
       B.parent = p;
       B.isLeftChild = false;
     }

     //p，q的关系
     q.left = p;
     p.parent = q;
     p.isLeftChild = true;

     //p和pp的关系
     q.parent = pp;
     //p是根节点
     if (pp == null) {
       root = q;
       return;
     }

     if (pIsLeft) {
       pp.left = q;
       q.isLeftChild = true;
     } else {
       pp.right = q;
       q.isLeftChild = false;
     }
   }

   @Override
   public void remove(K key) {
     removeNode(lookupNode(key));
     size--;// 记得减少元素个数
   }

   protected void removeNode(BSTNode<K, V> x) {
     if (x != null) {
       if (x.left == null && x.right == null) {// leaf node.  第一种情况 没有子节点
         if (x.parent == null) {
           root = null;
           return;
         }
         if (x.isLeftChild) {
           x.parent.left = null;
         } else {
           x.parent.right = null;
         }
         x.parent = null;
         x = null;
       } else if (x.left == null) {// 第二种情况 有子节点,但左子为空,有右孩子
         if (x.isLeftChild) {
           BSTNode<K, V> c = x.right;
           BSTNode<K, V> parent = x.parent;
           parent.left = c;
           c.isLeftChild = true;
           c.parent = parent;
         } else {
           if (x.parent != null) {
             x.parent.right = x.right;
             x.right.parent = x.parent;
           } else {// 根节点
             root = x.right;
           }
         }
         x = null;
       } else if (x.right == null) {// 第三种情况 有子节点,但右子为空，有左孩子
         if (x.isLeftChild) {
           x.parent.left = x.left;
           x.left.parent = x.parent;
         } else {
           if (x.parent != null) {
             x.parent.right = x.left;
             x.left.isLeftChild = false;
             x.left.parent = x.parent;
           } else { // 根节点
             root = x.left;
           }
         }
         x = null;
       } else {                // 第四种情况 都不为空
         BSTNode<K, V> minOfRight = minNode(x.right);
         x.key = minOfRight.key;// 更换x的内容
         removeNode(minOfRight); // 删掉右子树种最小的元素
       }
     }
   }

   // 有右子树 ，则后继为右子树最小
   // 否则往上回溯，找到一个是左结点的祖先，则后继是该结点的父亲
   @Override
   public K successor(K x) {
     BSTNode<K, V> xNode = lookupNode(x);
     if (xNode == null) {
       return null;
     }
     BSTNode<K, V> yNode = successor(xNode);
     return yNode == null ? null : yNode.key;

   }

   protected BSTNode<K, V> successor(BSTNode<K, V> xNode) {
     if (xNode == null) {
       return null;
     }
     if (xNode.right != null) {
       return minNode(xNode.right);
     }
     BSTNode<K, V> yNode = xNode.parent;
     while (yNode != null && xNode == yNode.right) {
       xNode = yNode;
       yNode = yNode.parent;
     }
     return yNode;
   }

   // 与找后继结点对称
   @Override
   public K predecessor(K x) {
     BSTNode<K, V> xNode = lookupNode(x);
     if (xNode == null) {
       return null;
     }
     if (xNode.left != null) {
       return maxNode(xNode.left).key;
     }
     BSTNode<K, V> yNode = xNode.parent;
     while (yNode != null && xNode.isLeftChild) {
       xNode = yNode;
       yNode = yNode.parent;
     }
     return yNode == null ? null : yNode.key;
   }

   @Override
   public boolean isBalance() {
     return !unBalance(root);
   }

   protected boolean unBalance(BSTNode g) {
     if (g == null) return false;
     int minus = getHeight(g.left) - getHeight(g.right);
     return Math.abs(minus) > 1
         || unBalance(g.right)
         || unBalance(g.left);
   }

   /**
    * 获取树的节点数
    * @return
    */
   @Override
   public int getSize() {
     return size;
   }

   @Override
   public int getHeight() {
     return getHeight(root);
   }

   protected int getHeight(BSTNode node) {
     if (node == null) return 0;
     int l = getHeight(node.left);
     int r = getHeight(node.right);
     return 1 + Math.max(l, r);
   }

   public List<List<BSTNode<K, V>>> levelOrder(BSTNode<K, V> x) {
     // int num=x.num;//累进的编号
     List<List<BSTNode<K, V>>> res = new ArrayList<>();
     Queue<BSTNode<K, V>> q = new LinkedList<>();
     q.add(x);
     BSTNode<K, V> last = x;
     BSTNode<K, V> nLast = null;
     List<BSTNode<K, V>> l = new ArrayList<>();
     res.add(l);
     while (!q.isEmpty()) {
       BSTNode<K, V> peek = q.peek();
       //把即将弹出的节点的子节点加入队列
       if (peek.left != null) {
         peek.left.num = peek.num * 2;
         q.add(peek.left);
         nLast = peek.left;
       }
       if (peek.right != null) {
         peek.right.num = peek.num * 2 + 1;
         q.add(peek.right);
         nLast = peek.right;
       }

       l.add(q.poll());//弹出,加入到当前层列表
       if (peek == last && !q.isEmpty()) {//如果现在弹出的节点是之前标记的最后节点，就要换列表
         l = new ArrayList<>();
         res.add(l);
         last = nLast;
       }
     }
     return res;
   }

   // 层次遍历
   @Override
   public List<List<BSTNode<K, V>>> levelOrder() {
     root.num = 1;
     return levelOrder(root);
   }

   // 按照格式打印
   @Override
   public String toString() {
     StringBuilder res = new StringBuilder();
     List<List<BSTNode<K, V>>> lists = levelOrder();
     int level = 1;
     int height = getHeight();
     for (List<BSTNode<K, V>> l :
         lists) {
       int gap = ex(2, height - level) - 1;//gap
       // printGap(gap);//打印左边margin
       int beginNum = ex(2, level - 1);
       for (BSTNode<K, V> node : l) {
         while (beginNum != node.num) {
           //打印gap
           for (int i = 0; i < 2 * gap; i++) {
             res.append(" ");
           }
           res.append("**");
           //打印gap
           for (int i = 0; i < 2 * gap; i++) {
             res.append(" ");
           }
           res.append("  ");
           beginNum++;
         }
         //打印gap
         for (int i = 0; i < 2 * gap; i++) {
           res.append(" ");
         }
         res.append(node.key);
         //打印gap
         for (int i = 0; i < 2 * gap; i++) {
           res.append(" ");
         }
         res.append("  ");

         beginNum++;
       }
       level++;
       res.append("\n");
     }
     return res.toString();
   }

   private void printGap(int margin) {
     for (int i = 0; i < margin; i++) {
       System.out.print(" ");
     }
   }

   private void printGap(int gap, String s, int gap1) {
     for (int i = 0; i < gap; i++) {
       System.out.print(" ");
     }
     System.out.printf("%2s", s);
     for (int i = 0; i < gap; i++) {
       System.out.print(" ");
     }

   }

     public static int ex(int a, int n) {
         if (n == 0)
             return 1;
         if (n == 1)
             return a;
         int temp = a; // a 的 1 次方
         int res = 1;
         int exponent = 1;
         while ((exponent << 1) < n) {
             temp = temp * temp;
             exponent = exponent << 1;
         }

         res *= ex(a, n - exponent);

         return res * temp;
     }
 }