OO-第一单元总结

经过了前三次作业和两次实验的引导，我的编程思路在逐步从面向过程转向面向对象。也对面向对象有了初步的理解。虽然第一次实验由于自己没有及时完成导致没有提交过有些遗憾，但是第二次实验还是提交了几次的（虽然由于时间原因并没有做好本地测试）。在三次作业中，总是有一些本可避免的小问题。在以后的学习中应该尽量避免犯这种错误。还有一些错误是由于自己改了后面的没有再次测试之前的数据引起的，以后在提交之前要尽量自己多做测试。

·基于度量分析自己的程序结构

第一次作业

　　

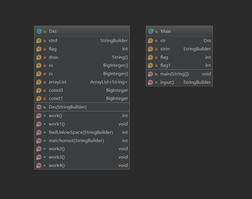
　　在第一次作业中我的思路主要是使用在 + - 符号前添加空格，将多项式分解为单项式进行求导。（并没有用到面向对象的思想

第二次作业

　　

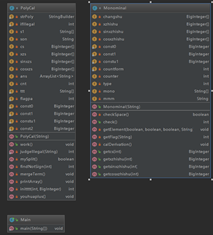
　　在第二次作业中，我的思路与第一次一样，还是将多项式使用 +- 分解为单项式，并将单项式使用在 * 前添加空格的方法分解为因子，并且对因子进行求导。实际在单项式求导中使用的是数组，用来将各因子的幂次及系数存起来，最后相乘（由于没有嵌套因子这样做十分方便，且最终只会有4个因子，即常数，sin(x),cos(x),x）,但这种结构在第三次作业中无法很好的复用。

第三次作业

　　

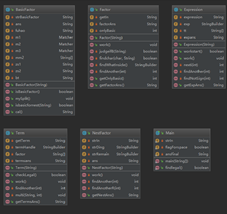
　　在第三次作业中，我的思路还是将表达式先分解成单项式，再将单项式分解为因子，然后判断此因子是什么类型，如果是简单因子则直接求导；如果是嵌套因子则传入嵌套因子类中，在嵌套因子类中去掉一层，保留求导后结果并将剩余部分传入表达式类，新形成新的表达式并求导；如果是表达式因子则去掉一层括号，并传入表达式类中。本次本意是要使用继承关系的，但是由于使用不熟练，并且想不清楚哪些属性，哪些方法需要继承，最终放弃。

·分析自己程序的bug

　　在第三次作业的过程中，发现了static不能乱用。。。之前的作业中，每个类里面写为static并无影响。但是第三次，如果类中private变量写为了static，则会引起递归无法进行下去，"被static修饰的变量或者方法是独立于该类的任何对象，也就是说，这些变量和方法不属于任何一个实例对象，而是被类的实例对象所共享。"

　　第一次作业中，有两个bug，分别是长度判断错误（>=1000 错判断为>1000）和未注意trim（），误以为trim只会删去首尾空格（实际上会删去首尾小于空格的所有空白字符）；

第二次作业中，也有两个bug，第一个是判断是否要在 - 号后面添加1，第二个是在合并同类项 sin(x)^2 + cos(x)^2  时引起的，没有判断两者的cos(x) 项和sin(x)项是否次数为0；

第三次作业中，错误主要是由于使用 +- 号分开多项式跳过*与^后的+-号条件错误，并且判断嵌套因子时里面是表达式因子的情况没有考虑完全。

　　总而言之，大部分错误是自己没有进行充分测试引起的，以后会尽量避免这种问题。

·分析自己发现别人程序bug所采用的策略

　　由于还没有学习对拍。发现别人bug主要是依靠将自己错误过的，编写程序时写出的样例在别人的程序中进行测试。还有少部分bug通过读别人的代码发现。

·总结

　　在三周的学习过程中，虽然紧张，但使我收获颇丰。特别是在互测阶段，（虽然被刀了很多同质bug...)但是可以看到互测屋中大佬的代码，可以学习他们写的好的地方。在以后的学习中，会加强自己的本地测试，尽量避免出现低级错误。如果进行第三次作业的重构的话我认为我的程序可以从添加一个factor父类，以供所有因子继承，还有可以添加乘法和加法接口，这样可以直接调用此接口来做乘法和加法运算，不用在每个类中再写加法方法和乘法方法。