从ranknet到lamdarank，再到lamdamart

learn2rank目前基本两个分支，1是神经网络学派ranknet，lamdarank，另一个是决策树学派如gbrank,lamdamart

05年提出ranknet，算分模块是简单的全连接网络，loss函数是预测概率之家的pair-wise关系和真实lablel的pair-wise关系的逻辑回归。

预测概率的pair-wise关系是两个相减然后求个sigmoid，如下图：

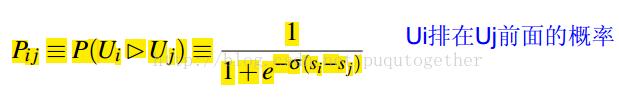
真实概率如下）（S_ij表示，i 比 j 相关，S_ij是1，反之是 -1，如果label一样是0）：

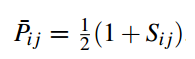
最后的loss是

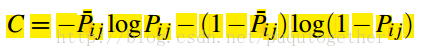
然后可以化简为：

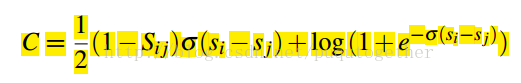
具体推倒过程见：

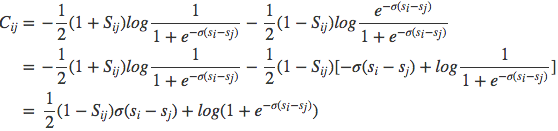
下面展示了当Sij分别取1，0，-1的时候cost function以si-sj为变量的示意图：

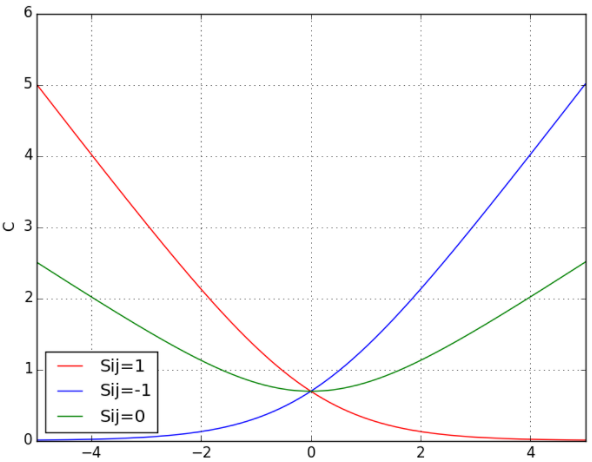
当两个相关性不同的文档算出来的模型分数相同时，损失函数的值大于0，仍会对这对pair做惩罚，使他们的排序位置区分开。

lamdarank想要解决的一个问题是，目前loss只会优化pair之间的关系，但是rank的目的是希望把最好好的结果往上promote，pair-wise没有考虑到这一点，使得最好的结果在中间位置也会loss非常小：

如：

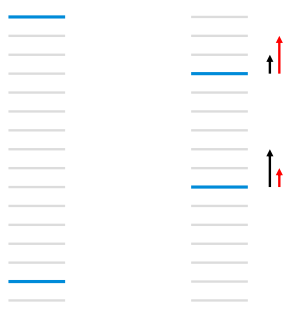
每个线条表示文档，蓝色表示相关文档，灰色表示不相关文档，RankNet以pairwise error的方式计算cost，左图的cost为13，右图通过把第一个相关文档下调3个位置，第二个文档上条5个位置，将cost降为11，但是像NDCG或者ERR等评价指标只关注top k个结果的排序，在优化过程中下调前面相关文档的位置不是我们想要得到的结果。图 1右图左边黑色的箭头表示RankNet下一轮的调序方向和强度，但我们真正需要的是右边红色箭头代表的方向和强度，即更关注靠前位置的相关文档的排序位置的提升。LambdaRank正是基于这个思想演化而来，其中Lambda指的就是红色箭头，代表下一次迭代优化的方向和强度，也就是梯度。

于是lamdarank在每个pair-wise loss乘以了一个ndcg的变化值，作为最终的loss

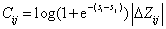
我的理解：如果是 i,j是预测对了，由于log项非常小，所以整体loss小，但是如果预测错了，会根据ndcg的差对loss加权，一般label比较大的权重也大

最后说说lamdamart，由于神经网络系列的模型都是可以直接求梯度的，Loss对模型也可以求梯度，所以很直接的用梯度下降就可以求解。

但是树模型由于无法直接求导，导致无法直接走梯度下降那一套进行求导。需要考虑另一种方法。

我们直接loss对模型可以直接求导的，那么我们就用model(i) = model(i-1) - Loss(梯度)。来求解最终的model就行了。由于树是ensemble的方式，实际使用的过程是model(i) = model(i-1)- (-loss(梯度))，即优化的时候，是减去loss的负梯度。

所以关键是每次迭代的时候是拟合 loss的负梯度，loss对于模型的负梯度是可以求出的(Loss = loss_function(model)，loss_function是可以求梯度的)，剩下来的就是模型来拟合这个梯度。这个梯度可以代表的是每个样本在一个函数的值，只是现在函数不是线性的，用树来拟合这些个值的话，其实就是树来求解一个回归问题，它也只能求解一个回归问题。不知道给你绕晕了没有，详细参考libo的文章吧

基本步骤就是，根据loss去求解当前的梯度值，然后用树模型来拟合梯度，加这个树后，重新进行迭代。

树拟合的过程就是分裂的过程，不多说，参考gbdt基本原理，就是每次分裂的时候使用左叶子节点值的和除以左叶子节点数目，加上右叶子节点值的和除以右叶子节点数目。看哪个特征分裂后这个值大就用这个特征进行分裂。分裂终止的条件就是根据你的设置叶子节点数目，或者分裂到叶子节点的样本数目少于多少等等。lightgbm分裂是所有叶子节点一起比较，选择一个最优的叶子节点进行分裂。xgboost是所有叶子节点都分类，是一个完全二叉树