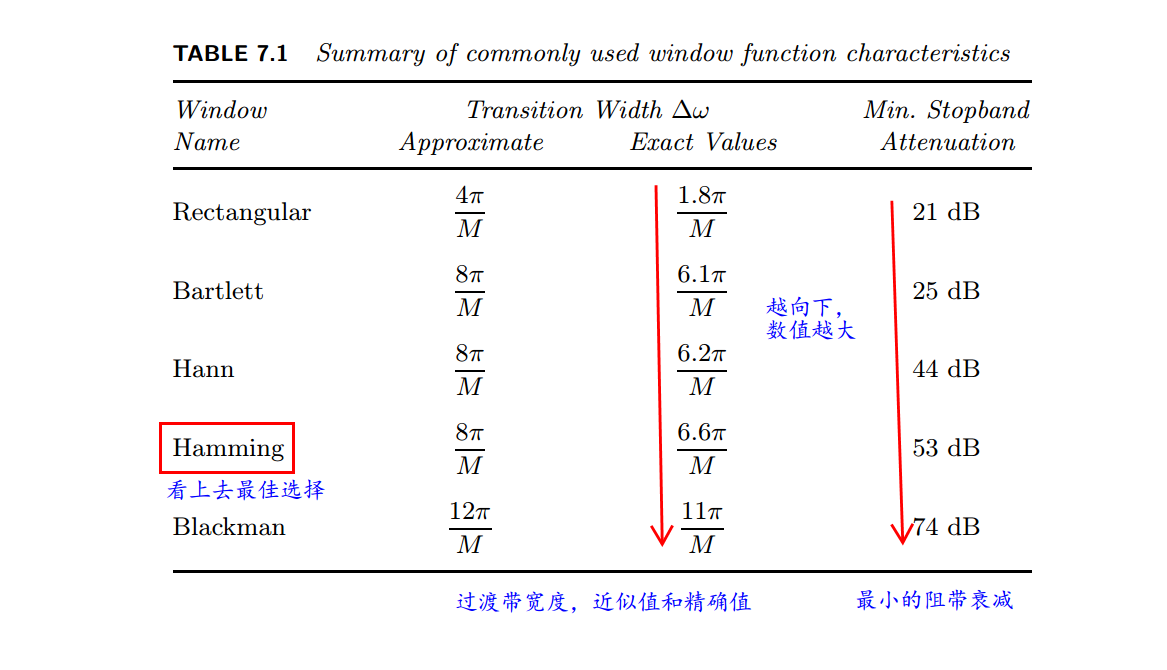
窗函数法设计FIR滤波器参数特征表的更多相关文章

  1. 使用MATLAB设计FIR滤波器

    1.      采用fir1函数设计,fir1函数可以设计低通.带通.高通.带阻等多种类型的具有严格线性相位特性的FIR滤波器.语法形式: b = fir1(n, wn) b = fir1(n, wn ...

  2. Quartus设计FIR滤波器的系数文件格式（适用于FIR II的IP核）

    对常用的FIR,我们使用MATLAB的fdatool(或者filterDesigner) 设计滤波器,给定指标,生成系数.为了方便,我们将系数保存到文件,其保存格式比较简介,在此进行说明. 1.FIR ...

  3. 转载论文关于fir滤波器的fpga实现

    摘 要 本文讨论的FIR滤波器因其具有严格的线性相位特性而得到广泛的应用.在工程实践中,往往要求信号处理具有实时性和灵活性,本论文研究FIR的FPGA解决方案正体现了电子系统的微型化和单片化. 本论文 ...

  4. FIR滤波器设计

    FIR滤波器的优越性: 相位对应为严格的线性,不存在延迟失真,仅仅有固定的时间延迟: 因为不存在稳定性问题,设计相对简单: 仅仅包括实数算法,不涉及复数算法,不须要递推运算,长度为M,阶数为M-1,计 ...

  5. FIR滤波器（1）- 基础知识

    FIR滤波器广泛应用于数字信号处理中,主要功能就是将不感兴趣的信号滤除,留下有用信号.FIR滤波器是全零点结构,系统永远稳定:并且具有线性相位的特征,在有效频率范围内所有信号相位上不失真.在无线通信收 ...

  6. CIC and Fir 滤波器的级联

    在FDATool中 CIC 和 Fir 级联滤波器的设计 1 设计CIC滤波器的幅频特性曲线如下 2.设计FIR 滤波器的幅频特性曲线如下 3.总的特性曲线如下 4.把通带部分放大后的图,比较平坦

  7. 数字信号处理实验（六）——FIR滤波器的设计

    一.四种线性相位FIR滤波器的振幅响应 1.自编函数 [Hr,w,a,L]=-n) [Hr,w,a,L]=-n) [Hr,w,a,L]=-n) [Hr,w,a,L]=-n) 2.一个demo clea ...

  8. matlab进行FIR滤波器设计（一）

    来源:https://blog.csdn.net/leokingszx/article/details/80041910 在实际的应用中,有时需要使用FIR根据完成一些特定功能,比如近似一阶RC低通电 ...

  9. IIR滤波器和FIR滤波器的区别与联系zz

      -------------------------------------------------------------------------------------------------- ...

随机推荐

  1. JavaEE第六周

    Applet简介 Java Applet简介 最近要使用worldwind java sdk做Applet开发,看了些Applet的资料,为了防止忘记,记录如下: applet是通过<apple ...

  2. 下载、安装 SQL server 2012，一步一步教你安装、激活sql server2012数据库 ，附有数据库安装包

    一. 准备阶段:下载2012 SQl server数据库安装包. 链接如下: 文件名:sql2012.zip 百度云链接:https://pan.baidu.com/s/1-fw1dCVbfU1bKM ...

  3. 记录Linux CentOS 7系统完整部署Docker容器环境教程

    笔者之前有在"详细介绍Ubuntu 16.04系统环境安装Docker CE容器的过程"文章中有介绍到利用Ubuntu系统安装Docker容器环境的过程.如果我们有使用CentOS ...

  4. while循环与 for循环

    import turtle turtle.setup(600,400,0,0) turtle.bgcolor('red') turtle.color('yellow') turtle.fillcolo ...

  5. L1-059 敲笨钟

    微博上有个自称“大笨钟V”的家伙,每天敲钟催促码农们爱惜身体早点睡觉.为了增加敲钟的趣味性,还会糟改几句古诗词.其糟改的方法为:去网上搜寻压“ong”韵的古诗词,把句尾的三个字换成“敲笨钟”.例如唐代 ...

  6. Input标签_实现限制输入字符类型(只能输入特定类型字符)

    ... <input type="text" placeholder="密码" maxlength="20" onKeyPress=& ...

  7. mysql建表时

    问题:Incorrect column specifier for column 'id' 答案:原来自动增长列用int数据类型,不用varchar

  8. JS 返回上一页并刷新代码整理

    一:JS 重载页面,本地刷新,返回上一页: <a href="javascript:history.go(-1)">返回上一页</a> <a href ...

  9. Python机器学习（python简介篇）

    1.Python 数据类型 Python 内置的常用数据类型共有6中: 数字(Number).布尔值(Boolean).字符串(String).元组(Tuple).列表(List).字典(Dictio ...

  10. MySQL 把两个结果集拼接到一起（两个结果集的列一模一样）

    select * from a UNION all ( select * from b)