[LeetCode] Domino and Tromino Tiling 多米诺和三格骨牌

We have two types of tiles: a 2x1 domino shape, and an "L" tromino shape. These shapes may be rotated.

XX  <- domino

XX  <- "L" tromino
X

Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.

(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)

Example:
Input: 3
Output: 5
Explanation:
The five different ways are listed below, different letters indicates different tiles:
XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY

Note:

• N  will be in range [1, 1000].

这道题是关于多米诺骨牌和三格骨牌的，其中由两个方形格子组成的是多米诺骨牌（音译，即为双格骨牌），而由三个方形格子组成的‘L’型的是三格骨牌，但其实本质还是个拼格子的问题，并没有利用到骨牌酷炫的连倒技能，倒反而更像是俄罗斯方块中的形状。说是有一个2xN大小的棋盘，我们需要用这些多米诺和三格骨牌来将棋盘填满，问有多少种不同的填充方法，结果需要对一个超大数取余。那么根据博主多年的经验，对于这种求极值，并且超大的情况下，只能使用动态规划Dynamic Programming来做，什么暴力递归神马的，等着爆栈吧。

既然决定了要用DP来做，那么首先就来设计dp数组吧，这里我们就用一个一维的dp数组就行了，其中dp[i]表示填满前i列的不同填法总数对超大数10e^9+7取余后的结果。那么DP解法的难点就是求状态转移方程了，没什么太好的思路的时候，就从最简单的情况开始罗列吧。题目中给了N的范围是[1, 1000]，那么我们来看：

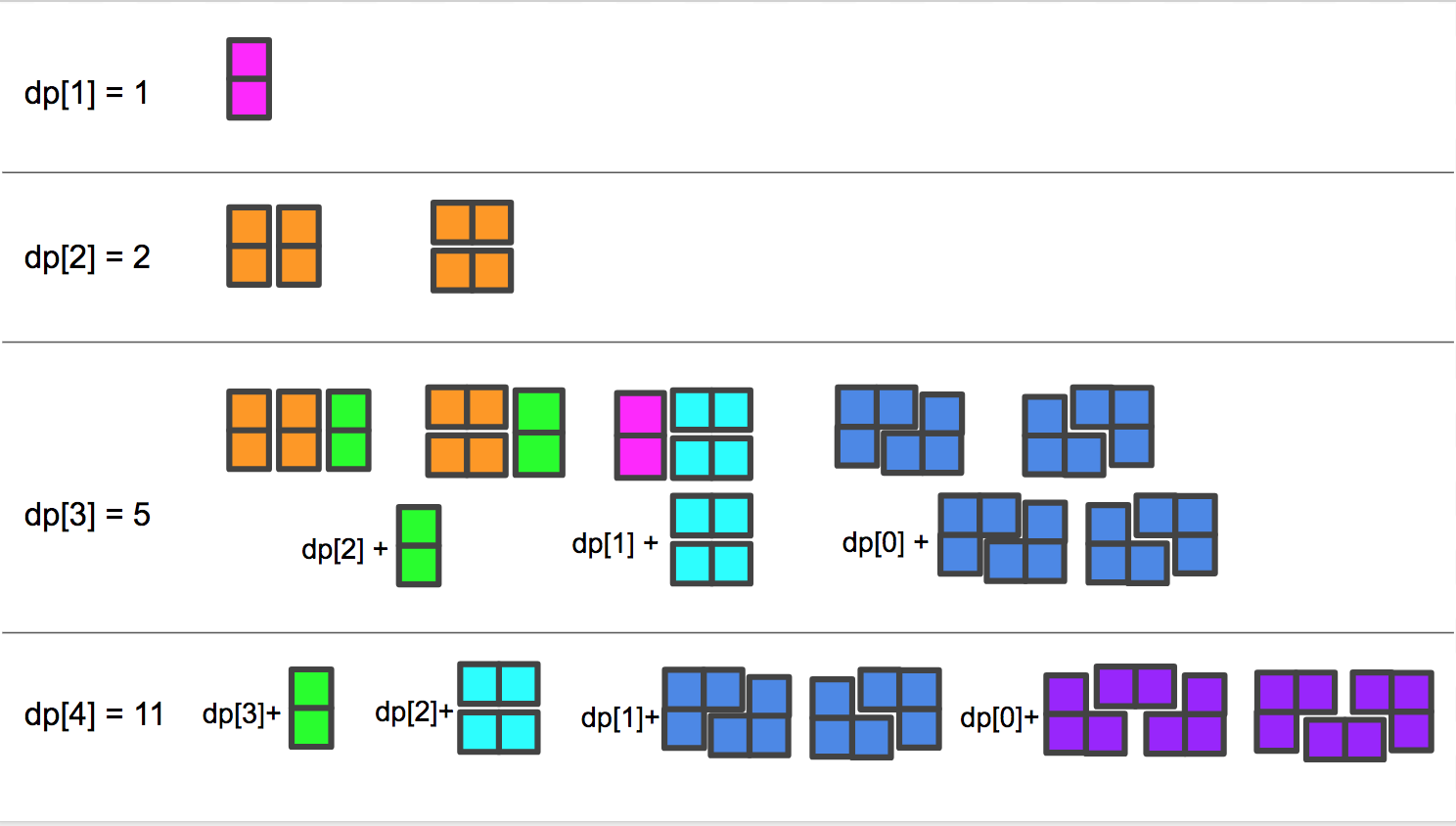
当N=1时，那么就是一个2x1大小的棋盘，只能放一个多米诺骨牌，只有一种情况。

当N=2时，那么就是一个2x2大小的棋盘，如下图所示，我们有两种放置方法，可以将两个多米诺骨牌竖着并排放，或者是将其横着并排放。

当N=3时，那么就是一个3x2大小的棋盘，我们共用五种放置方法，如下图所示。仔细观察这五种情况，我们发现其时时跟上面的情况有联系的。前两种情况其实是N=2的两种情况后面加上了一个竖着的多米诺骨牌，第三种情况其实是N=1的那种情况后面加上了两个平行的横向的多米诺骨牌，后两种情况是N=0（空集）再加上两种三格骨牌对角摆开的情况。

当N=4时，那么就是一个4x2大小的棋盘，我们共用十一种放置方法，太多了就不一一画出来了，但是其也是由之前的情况组合而成的。首先是N=3的所有情况后面加上一个竖着多米诺骨牌，然后是N=2的所有情况加上两个平行的横向的多米诺骨牌，然后N=1再加上两种三格骨牌对角摆开的情况，然后N=0（空集）再加上两种三格骨牌和一个横向多米诺骨牌组成的情况。

N=5的情况博主没有再画了，可以参见ZhengKaiWei大神的帖子中的手稿图，很萌～

根据目前的状况，我们可以总结一个很重要的规律，就是dp[n]是由之前的dp值组成的，其中 dp[n-1] 和 dp[n-2] 各自能贡献一种组成方式，而dp[n-3]，一直到dp[0]，都能各自贡献两种组成方式，所以状态转移方程呼之欲出：

dp[n] = dp[n-1] + dp[n-2] + 2 * (dp[n-3] + ... + dp[0])

= dp[n-1] + dp[n-3] + dp[n-2] + dp[n-3] + 2 * (dp[n-4] + ... dp[0])

= dp[n-1] + dp[n-3] + dp[n-1]

= 2 * dp[n-1] + dp[n-3]

最后化简后的形式就是最终的状态转移方程了，是不是叼的飞起～

class Solution {
public:
    int numTilings(int N) {
        int M = 1e9 + ;
        vector<long> dp(N + );
        dp[] = ; dp[] = ; dp[] = ;
        for (int i = ; i <= N; ++i) {
            dp[i] = (dp[i - ] *  + dp[i - ]) % M;
        }
        return dp[N];
    }
};

参考资料：

https://leetcode.com/problems/domino-and-tromino-tiling/discuss/116513/Java-solution-DP

https://leetcode.com/problems/domino-and-tromino-tiling/discuss/116581/Detail-and-explanation-of-O(n)-solution-why-dpn2*dn-1+dpn-3

https://leetcode.com/problems/domino-and-tromino-tiling/discuss/116664/Schematic-explanation-of-two-equivalent-DP-recurrence-formula

LeetCode All in One 题目讲解汇总(持续更新中...)