[luogu P3960] [noip2017 d2t3] 队列

[luogu P3960] [noip2017 d2t3] 队列

题目描述

Sylvia 是一个热爱学习的女♂孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有n \times mn×m名学生，方阵的行数为 nn，列数为 mm。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 1 到 n \times mn×m 编上了号码（参见后面的样例）。即：初始时，第 ii 行第 jj 列 的学生的编号是(i-1)\times m + j(i−1)×m+j。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 qq件这样的离队事件。每一次离队事件可以用数对(x,y) (1 \le x \le n, 1 \le y \le m)(x,y)(1≤x≤n,1≤y≤m)描述，表示第 xx 行第 yy 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达 这样的两条指令：

1. 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 xx 行第 mm 列。

2. 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 nn 行第 mm 列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 nn 行 第 mm 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学 的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后 方阵中同学的编号可能是乱序的。

输入输出格式

输入格式：

输入共 q+1q+1 行。

第 1 行包含 3 个用空格分隔的正整数 n, m, qn,m,q，表示方阵大小是 nn 行 mm 列，一共发 生了 qq 次事件。

接下来 qq 行按照事件发生顺序描述了 qq 件事件。每一行是两个整数 x, yx,y，用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 xx 行第 yy 列。

输出格式：

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学 生的编号。

输入输出样例

输入样例#1： 复制

2 2 3
1 1
2 2
1 2 

输出样例#1： 复制

1
1
4

说明

【输入输出样例 1 说明】

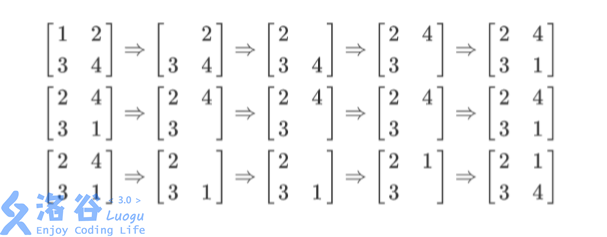
列队的过程如上图所示，每一行描述了一个事件。 在第一个事件中，编号为 1 的同学离队，这时空位在第一行第一列。接着所有同学 向左标齐，这时编号为 2 的同学向左移动一步，空位移动到第一行第二列。然后所有同 学向上标齐，这时编号为 4 的同学向上一步，这时空位移动到第二行第二列。最后编号 为 1 的同学返回填补到空位中。

【数据规模与约定】

数据保证每一个事件满足 1 \le x \le n,1 \le y \le m1≤x≤n,1≤y≤m

sol明天补。。

upd：

首先，注意到nm都很大，怎么办？看似无从下手。

而注意到每一次操作都分2个阶段。

第一个阶段是修改(x,y)~(x,m)，第二个阶段是修改(x,m)~(n,m)。

注意到这些操作又可以细分：

1.将(x,y)拿出并删除；

2.将(x,y+1)~(x,m)向前一格补上；

3.将(x,m+1)~(n,m)向上一格补上。

我们可以这样想，总操作次数是1e5级别的，说明改动次数少。

一次改动相当于把一个区间分为3段，删掉中间一段。这样，最后形成的总段数也不多。

又想到，splay能维护区间，那我们就可以建一堆splay，分别维护每一行的区间情况（当然要动态维护）。

又由于最后一列特殊，普通做法我们需要扫一遍每一个涉及到的行，效率底下。不如单独拉出来做一棵splay?

所以，最后我们要建n+1棵splay，每个splay中的每个节点表示一个区间。

其中对于第i棵(1<=i<=n)的节点，维护一个l，r，代表区间（化为一维编号）。

对于维护最后一列的splay，为了方便操作，也维护一个区间（单点成区间）。

然后我们需要的大操作有split，merge，splay，insert和erase。

具体实现可见代码。

code：

 %:pragma GCC optimize()
 #include <cstdio>
 #include <iostream>
 typedef long long LL;

 void OJ_file() {
     #ifndef ONLINE_JUDGE
         freopen("in.txt","r",stdin);
         freopen("out.txt","w",stdout);
     #endif
 }

 namespace fastIO {
     #define puc(c) putchar(c)
     inline int read() {
         ; char ch=getchar();
         ') ch=getchar();
         ') {
             x=(x<<)+(x<<)+ch-';
             ch=getchar();
         }
         return x;
     }
     ];
     template <class T> inline void write(T x) {
         ) {
             puc('); return;
         }
         ; x; x/=) w[++cnt]=x%;
         );
     }
     inline void newline() {
         puc('\n');
     }
 } using namespace fastIO;

 ;
 int n,m,q;

 #define SplayTree node
 struct SplayTree {
     int s; LL l,r;
     node* c[];
     node () {
         s=l=r=;
         c[]=c[]=c[]=;
     }
 }*ro[N],*an;
 void newnode (node* &x,LL l,LL r) {
     x=,x->l=l,x->r=r;
 }
 #define M ((l)+(r)>>1)
 void setup (node* &x,LL l,LL r) {
     newnode(x,l,r);
 }
 int len (node* x) {
     :;
 }
 bool dir (node* x) {
     ]) ;
     ]->c[]==x;
 }
 void refresh (node* x) {
     x->s=len(x);
     ]) x->s+=x->c[]->s;
     ]) x->s+=x->c[]->s;
 }
 void linknode (node* y,node* x,bool p) {
     ]=y;
     if (y) y->c[p]=x;
 }
 void rotate (node* x) {
     ];
     linknode(y->c[],x,dir(y));
     linknode(y,x->c[p^],p);
     linknode(x,y,p^);
     refresh(y),refresh(x);
 }
 void splay (node* x,int i) {
     ]==an) return;
     ]!=an) {
         ]->c[]==an) {
             rotate(x);
             if (!an) ro[i]=x;
             return;
         }
         rotate(dir(x)^dir(x->c[])?x:x->c[]);
         rotate(x);
     }
     if (!an) ro[i]=x;
 }
 void insert (int i,LL v) {
     node* x=ro[i];
     if (!x) {
         newnode(ro[i],v,v);
         linknode(,ro[i],);
         return;
     }
     ]) x=x->c[];
     splay(x,i);
     newnode(x,v,v);
     linknode(ro[i],x,);
     refresh(ro[i]);
 }
 node* split (node* x,int i,int k) {
     node* y,* t;
     ]) {
         newnode(y,x->l+k,x->r);
         linknode(x,y,);
         x->r=x->l+k-,refresh(x);
         splay(x->c[],i);
         return ro[i];
     }
     newnode(y,x->l+k,x->r);
     t=x,x=x->c[];
     ]) x=x->c[];
     linknode(x,y,);
     t->r=t->l+k-,refresh(t);
     splay(x->c[],i);
     return ro[i];
 }
 node* erase (int i,int k) {
     node* x=ro[i],* y; int s;
     ) {
         s=x->c[]?x->c[]->s:;
         ]; else {
             k-=s;
             if (k<=len(x)) break; else {
                 k-=len(x),x=x->c[];
             }
         }
     }
     if (k!=len(x)) split(x,i,k);
     ) x=split(x,i,k-);
     splay(x,i);
     newnode(y,x->l,x->l);
     ]) {
         linknode(,x->c[],dir(x));
         ro[i]=x->c[];
         return y;
     }
     x=x->c[];
     ]) x=x->c[];
     splay(x,i);
     ]) linknode(x,x->c[]->c[],);
     refresh(x);
     return y;
 }

 int main() {
     OJ_file();
     n=read(),m=read(),q=read(),an=;
     setup(ro[],m,m);
     ; i<=n; ++i) {
         setup(ro[i],(LL)(i-)*m+,(LL)i*m-);
     }
     ; i<=n; ++i) {
         insert(,(LL)i*m);
     }
     int X,Y; node* u;
     for (; q; --q) {
         X=read(),Y=read();
         u=erase(,X);
         insert(X,u->l);
         u=erase(X,Y);
         insert(,u->l);
         write(u->l),newline();
     }
     ;
 }