prefixspan是挖掘频繁子序列，子序列不一定是连续的，当心！！！

序列模式挖掘是从序列数据库中发现频繁子序列作为模式。

子序列与频繁序列

　　　　了解了序列数据的概念，我们再来看看上面是子序列。子序列和我们数学上的子集的概念很类似，也就是说，如果某个序列A所有的项集在序列B中的项集都可以找到，则A就是B的子序列。当然，如果用严格的数学描述，子序列是这样的：

　　　　对于序列A={a1,a2,...ana1,a2,...an}和序列B={b1,b2,...bmb1,b2,...bm},n≤mn≤m，如果存在数字序列1≤j1≤j2≤...≤jn≤m1≤j1≤j2≤...≤jn≤m, 满足a1⊆bj1,a2⊆bj2...an⊆bjna1⊆bj1,a2⊆bj2...an⊆bjn，则称A是B的子序列。当然反过来说， B就是A的超序列。

　　　　而频繁序列则和我们的频繁项集很类似，也就是频繁出现的子序列。比如对于下图，支持度阈值定义为50%，也就是需要出现两次的子序列才是频繁序列。而子序列<(ab)c>是频繁序列，因为它是图中的第一条数据和第三条序列数据的子序列，对应的位置用蓝色标示。

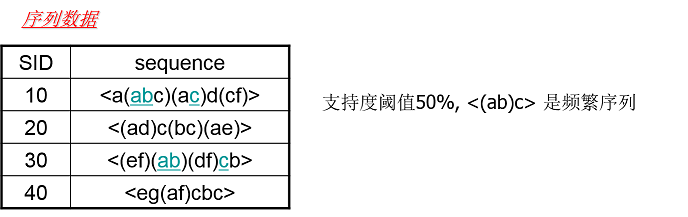
看到了吧，没有要求abc是必须连续的子列。

如何用在用户行为异常检测呢？？？？？既然不是连续子序列的话？？？？