MySQL 树形索引结构 B树 B+树

如何评估适合索引的数据结构

索引的本质是一种数据结构
内存只是临时存储，容量有限且容易丢失数据。因此我们需要将数据放在硬盘上。
在硬盘上进行查询时也就产生了硬盘的I/O操作，而硬盘的I/O存取消耗的时间要比读取内存大很多。因此数据查询的时间主要决定于I/O操作的次数。
每访问一次节点就需要对磁盘进行一次I/O操作。

树模型

二分查找的时间复杂度是O(log2n)，是一种很高效的查询方式。在一系类树种使用二分查找的树有很多，但并不是所有树都适合作为索引的结构。

Binary Search Tree 二叉搜索树（BST）

性质：

对任意节点，左子树不为空则左子树所有节点小于或等于该节点的值
对任意节点，右子树不为空则右子树所有节点大于或等于该节点的值

但二叉搜索树不一定是"平衡的"，它有可能退化成一条链表，那么他的搜索时间就变成了O(n)。

平衡二叉搜索树（AVL）

为了避免退化成一条链表，人们提出了二叉搜索树，AVL在二叉搜索树的基础上增加了约束：

每个节点的左子树和右子树的高度差不能超过1

也就是说要求节点的左右子树仍然为平衡二叉树。

常见的平衡二叉树有很多种，包括了AVL树、红黑树、数堆、伸展树。AVL树是最早提出来的自AVL树，当我们提到平衡二叉树时一般指的就是AVL树

左右平衡后就使得搜索时间复杂度能稳定在O(log2n)。

但是即便在理论上它的搜索效率高且比较稳定，但是由于“每访问一次节点就需要进行一次磁盘I/O操作”，在实际情况中只有两个子节点的情况下，树的高度依然有可能会很高，比如说现有一个五层共31个节点的树，那么我们需要进行5次I/O操作。

B Tree

既然"二叉"结构可能让树变得很高，那么我们自然而然地就明白可以让子节点数变得更多来减少I/O次数。在文件系统和部分数据库系统中，B树就已经得到了实际的应用。

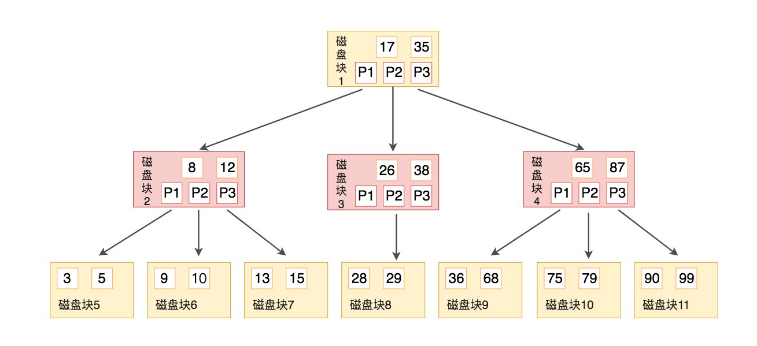
如图所示，B树有如下性质

B树也是平衡的，每个节点可以有M个子节点，M也称为B树的阶
每个磁盘块都包含着关键字和指针，有k-1个关键字，那么就有k个指针，也就是k个子节点。也就等同于子节点的数量=关键字数量+1
所有子节点都在同一层，且每个叶子节点没有子节点，只包含k-1个关键字
子节点和非子节点都即保存数据记录又保存索引。
k-1个关键字相当于划分出了k个范围，每个范围对应一个指针。

例如，有关键字Key[1], Key[2], …, Key[k-1]，且关键字按照升序排序

它们划分出k个范围对应k个指针，P[1], P[2], …, P[k]

对应关系就是：P[1]指向关键字小于 Key[1]的子树，P[i]指向关键字属于 (Key[i-1], Key[i]) 的子树，P[k]指向关键字大于 Key[k-1]的子树

在B树上的搜索过程就是：

要找目标关键字n，那么就从根节点开始，不断在树的每一层的每两个相邻关键字划定的范围中寻找包含目标关键字的节点，顺着索引一直寻找，直到某节点中关键字与目标关键字相同。

这里说的关键字在实际的数据库中，其实就是一条实际的数据或者主键值，详细可见此处

MongoDB内部使用的就是B树

B+ Tree

主流的RDMS大多采用B+树作为索引结构，包括MySQL的InnoDB引擎（不同存储引擎的索引的工作方式并不一样。而即使多个存储引擎支持同一种类型的索引，其底层的实现也可能不同）

在数据结构性质上与B树不同的是：

有K个孩子就有k个关键字。通俗来讲，B树是给每一个范围一个指针，而B+树是给每个子节点直接给一个指针。
只有叶子节点保存数据记录，非叶子节点仅用于索引
所有关键字都在叶子节点中。每层子节点的关键字也会保存在下一层子节点中且是子节点关键字中最大或最小的那一个，这样到最后，所有关键字都集合在叶子节点中。
叶子节点之间会按照关键字的大小从小到大，使用双向链表进行串联。支持了区间查询。

B+树 vs B树

上面说了两种数据结构性质上的不同，下面里对比下实际生产中两种索引结构的区别。

B+树查询效率更稳定。

B+树所有的数据记录都在叶子节点，而B树的数据记录可能在叶子节点也可能在非叶子节点，这样就会导致查询效率的不稳定。
B+树查询效率更高。

B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小。那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。
B+树的范围查询效率更高。

B+树所有叶子节点都通过双向链表进行查询，方便范围查询。

而B树因为在非叶子节点中也存有数据记录，因此范围查询时需要通过对树的中序遍历才能完成

其他索引见此