Graphviz 使用笔记

　　官网：Graphviz

　　最近一直在找如何用写代码的方式就可以实现数据结构可视化、流程图等等，于是发现了她，上手也比较简单，但正当我仅觉得不错的时候，我发现竟然还可以用python来写，瞬间好感度爆满啊！太激动了~

　　下面就先简单说一说Windows下如何使用吧：

　　首先不管是直接写digraph，还是用python，都必须要安装并配置好Graphviz，配置实际上都是常用的做法了，把dot.exe等文件路径添加到系统环境变量中的PATH即可。然后就可以用notepad等编辑器编写代码，保存时保存为 .gv 或 .dot 后缀，再用dot命令编译为pdf、png、jpg、jpeg等等即可。例如，编写内容如下：

digraph tree {
	node [shape=circle]
	67
	53
	79
	46
	57
	70
	88
	43
	55
	60
	74
	56
	67 -> 53
	67 -> 79
	53 -> 46
	53 -> 57
	79 -> 70
	79 -> 88
	46 -> 43
	57 -> 55
	57 -> 60
	55 -> 56
	70 -> 74
}

　　然后键入dot命令：

　　如果没有报错，则可以打开tree.png了:

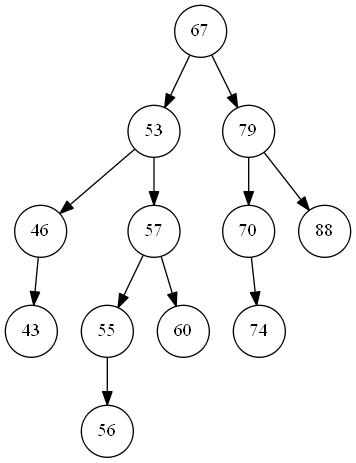
　　使用python编写graphviz还需要使用pip来安装一个包：

$ pip install graphviz

　　然后就参考这篇文档来学习吧。

　　一个例子：

from graphviz import Digraph, Graph

dot = Digraph(name='tree', node_attr={'shape': 'circle'})

dot.node('67')
dot.node('53')
dot.node('79')
dot.node('46')
dot.node('57')
dot.node('70')
dot.node('88')
dot.node('43')
dot.node('55')
dot.node('60')
dot.node('74')
dot.node('56')

dot.edge('67', '53')
dot.edge('67', '79')
dot.edge('53', '46')
dot.edge('53', '57')
dot.edge('79', '70')
dot.edge('79', '88')
dot.edge('46', '43')
dot.edge('57', '55')
dot.edge('57', '60')
dot.edge('55', '56')
dot.edge('70', '74')
print(dot.source)
dot.render('avl-tree.gv', view=True)

　　这里我不知道为啥我配置好了路径，却运行最后还是会报找不到相应文件路径的错，但还是能生成'avl-tree.gv'文件，然后就只有手动在命令行编译文件了。

　　截图：

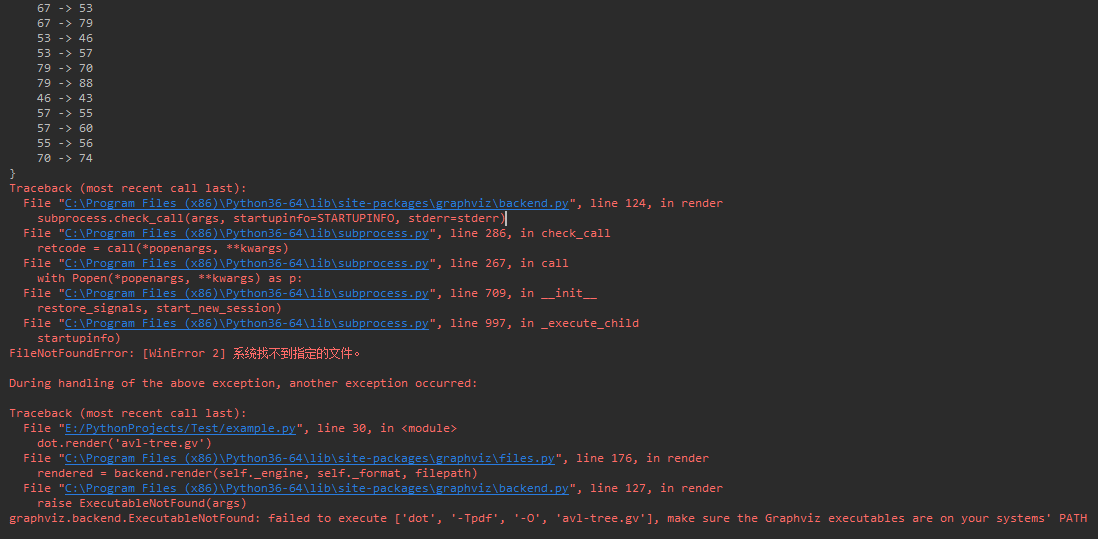
　　还是输出了.gv文件：

　　再来个例子：

from graphviz import Digraph

dot = Digraph(name='tree', filename='tree.gv', node_attr={'shape': 'circle'})
dot.node_attr.update(color='lightblue2', style='filled')

dot.edge('67', '53')
dot.edge('67', '79')
dot.edge('53', '46')
dot.edge('53', '57')
dot.edge('79', '70')
dot.edge('79', '88')
dot.edge('46', '43')
dot.edge('57', '55')
dot.edge('57', '60')
dot.edge('55', '56')
dot.edge('70', '74')

print(dot.source)

　　tree.png:

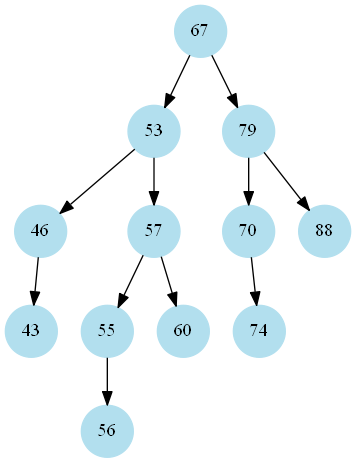
　　还可以再简单一些：

dot.edges([('67', '53'),
           ('67', '79'),
           ('53', '46'),
           ('53', '57'),
           ('79', '70'),
           ('79', '88'),
           ('46', '43'),
           ('57', '55'),
           ('57', '60'),
           ('55', '56'),
           ('70', '74')
           ])