96题--不同的二叉搜索树（java、中等难度）

题目描述：给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例如下：

分析：本题可用动态规划的方法求解。

　　设 dp[n] 表示以 1 ... n 为节点组成的二叉搜索树的种类，我们做如下讨论：

1）当头结点的值为1时，左子树为空，即左子树可能出现的二叉搜索树的结构数为1。右子树上有(n - 1)个结点，此时右子树(n-1)个结点可能组成的二叉搜索树的个数为 dp[n-1]。

那么总的可能出现的二叉搜索树的结构数 dp[n] = 左子树可能结构数 * 右子树可能结构数 = 1 * dp[n-1]；

2）当头结点的值为 i (1 < i < n) 时，左子树的结点为：1 —> i-1  ，这 (i-1) 个结点可能组成的二叉搜索树的个数为 dp[i-1]；右子树的结点为：i+1 —> n  ，这 (n-i) 个结点可能组成的二叉搜索树的个数为 dp[n-i].

那么，左右子树以及头结点 i 组成的二叉搜索树可能的结构种类为：dp[i] = dp[i-1] * dp[n-i]；

3）当头结点的值为n时，右子树为空，左子树上有(n - 1)个结点，此时左子树(n-1)个结点可能组成的二叉搜索树的个数为 dp[n-1]；

那么总的可能出现的二叉搜索树的结构数 dp[n] = dp[n-1] * 1；

　　另外，n = 0 时 dp[0] = 1，因为空树也算一种二叉搜索树；那么n = 1时的情况可以看做是其左子树可能结构数乘以右子树可能结构数，左右字数都是空树，所以1乘1还是1，dp[1]=1。

　　终上所述：dp[n] = dp[0] * dp[n-1] + dp[1] * dp[n-2] + ...... + dp[i-1]*dp[n-i] + ...... + dp[n-2] * dp[1] + dp[n-1] * dp[0] 。这实际上是一个卡特兰数问题。

　　

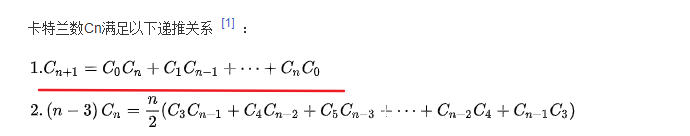
　　那么，根据以上递推公式，我们可以从0开始，求得每一个 dp[i]，这样就可以递推得到dp[n]，这种方法的时间复杂度是 O(n^2) ，因为代码内部有2层循环。

　　代码如下（java语言）：

     public int numTrees(int n)
     {
         //定义一个长度为 n+1 的数组，用于存储 dp[1] - dp[n]
         int[] dp = new int[n+1];
         dp[0] = 1;
         dp[1] = 1;

         //通过2层循环，i=2,...,n 找到每一个dp[i]
         for (int i = 2; i <= n ; i++)
         {
             for (int j = 0; j <= i-1 ; j++)
             {
                 dp[i] += dp[j] * dp[i-j-1];
             }
         }

         return dp[n];
     }