LeetCode #188场周赛题解

A题链接

给你一个目标数组 target 和一个整数 n。每次迭代，需要从 list = {1,2,3..., n} 中依序读取一个数字。

请使用下述操作来构建目标数组 target ：

• Push：从 list 中读取一个新元素， 并将其推入数组中。
• Pop：删除数组中的最后一个元素。
• 如果目标数组构建完成，就停止读取更多元素。

题目数据保证目标数组严格递增，并且只包含 1 到 n 之间的数字。

请返回构建目标数组所用的操作序列。

题目数据保证答案是唯一的。

示例 1

输入：target = [1,3], n = 3
输出：["Push","Push","Pop","Push"]
解释：
读取 1 并自动推入数组 -> [1]
读取 2 并自动推入数组，然后删除它 -> [1]
读取 3 并自动推入数组 -> [1,3]

示例 2：

输入：target = [1,2,3], n = 3
输出：["Push","Push","Push"]

示例 3：

输入：target = [1,2], n = 4
输出：["Push","Push"]
解释：只需要读取前 2 个数字就可以停止。

提示：

• 1 <= target.length <= 100
• 1 <= target[i] <= 100
• 1 <= n <= 100
• target 是严格递增的

class Solution {
public:
    //正常判断是否需要在target数组中存储，同时如果足够了即可break
    vector<string> buildArray(vector<int>& target, int n) {
        vector<string>v;
        int len = target.size();
        int j = 0;
        for(int i = 1;i <=n ;++i){
            if(j == len)break;
            if(i == target[j]){
                v.push_back("Push");
                ++j;
            }
            else{
                v.push_back("Push");
                v.push_back("Pop");
            }
        }
        return v;
    }
};

[B题](https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor/)

给你一个整数数组 arr 。

现需要从数组中取三个下标 i、j 和 k ，其中 (0 <= i < j <= k < arr.length) 。

a 和 b 定义如下：

• a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]
• b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]

注意：^ 表示 按位异或 操作。

请返回能够令 a == b 成立的三元组$ (i, j , k)$ 的数目。

示例 1：

输入：arr = [2,3,1,6,7]
输出：4
解释：满足题意的三元组分别是 (0,1,2), (0,2,2), (2,3,4) 以及 (2,4,4)

示例2：

输入：arr = [1,1,1,1,1]
输出：10

示例 3：

输入：arr = [2,3]
输出：0

思路：

arr[i]^...arr[j-1]的异或结果可以转化为(arr[0]^...arr[j-1])^(arr[0]...^arr[i-1])，因为相同的值异或为0，而异或一个0是不影响原结果的。因此事先计算出会用到的异或结果，用数组dp保存。

class Solution {
public:
    int countTriplets(vector<int>& a) {
        int n = a.size();
        vector<int> s(n+1);
        for (int i = 1; i <= n; ++ i)
            s[i] = s[i-1]^a[i-1];
        int ret = 0;
        for (int i = 1; i <= n; ++ i)
            for (int j = i+1; j <= n; ++ j)
                for (int k = j; k <= n; ++ k)
                {
                    if ((s[j-1]^s[i-1]) == (s[k]^s[j-1])) ret ++;
                }
        return ret;
    }
};

[C题](https://leetcode-cn.com/problems/minimum-time-to-collect-all-apples-in-a-tree/)

给你一棵有 n 个节点的无向树，节点编号为 0 到 n-1 ，它们中有一些节点有苹果。通过树上的一条边，需要花费 1 秒钟。你从 节点 0 出发，请你返回最少需要多少秒，可以收集到所有苹果，并回到节点 0 。

无向树的边由 edges 给出，其中 edges[i] = [fromi, toi] ，表示有一条边连接 from 和 toi 。除此以外，还有一个布尔数组 hasApple ，其中 hasApple[i] = true 代表节点 i 有一个苹果，否则，节点 i 没有苹果。

示例 1：

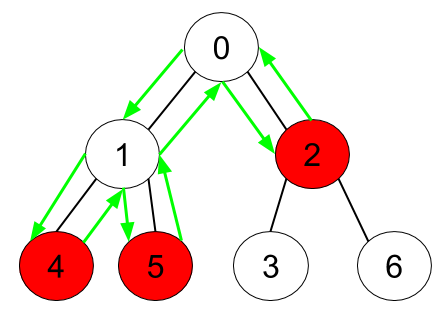
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
输出：8
解释：上图展示了给定的树，其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。

示例 2：

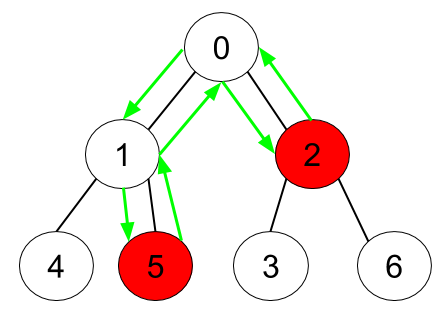
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
输出：6
解释：上图展示了给定的树，其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。

思路：

只要那个节点是true，向上一直将父节点同化，那么路径就等于：每两个连接（子、父都为true）的点的那条线x 2 后的和

class Solution {
public:
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        int i,res=0;
        //若子节点为true，则父节点同化为true
        for(i=edges.size()-1; i>=0; i--)
            if(hasApple[edges[i][1]]==true)
                hasApple[edges[i][0]]=true;
        // 收集苹果的路径即为所有节点为true的拓扑图的所有连线*2
        for(i=0; i<edges.size(); i++)
            if(hasApple[edges[i][1]]==true) res +=2;
        return res;
    }
};

D题

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： 'A' （表示苹果）和 '.' （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

示例 1：

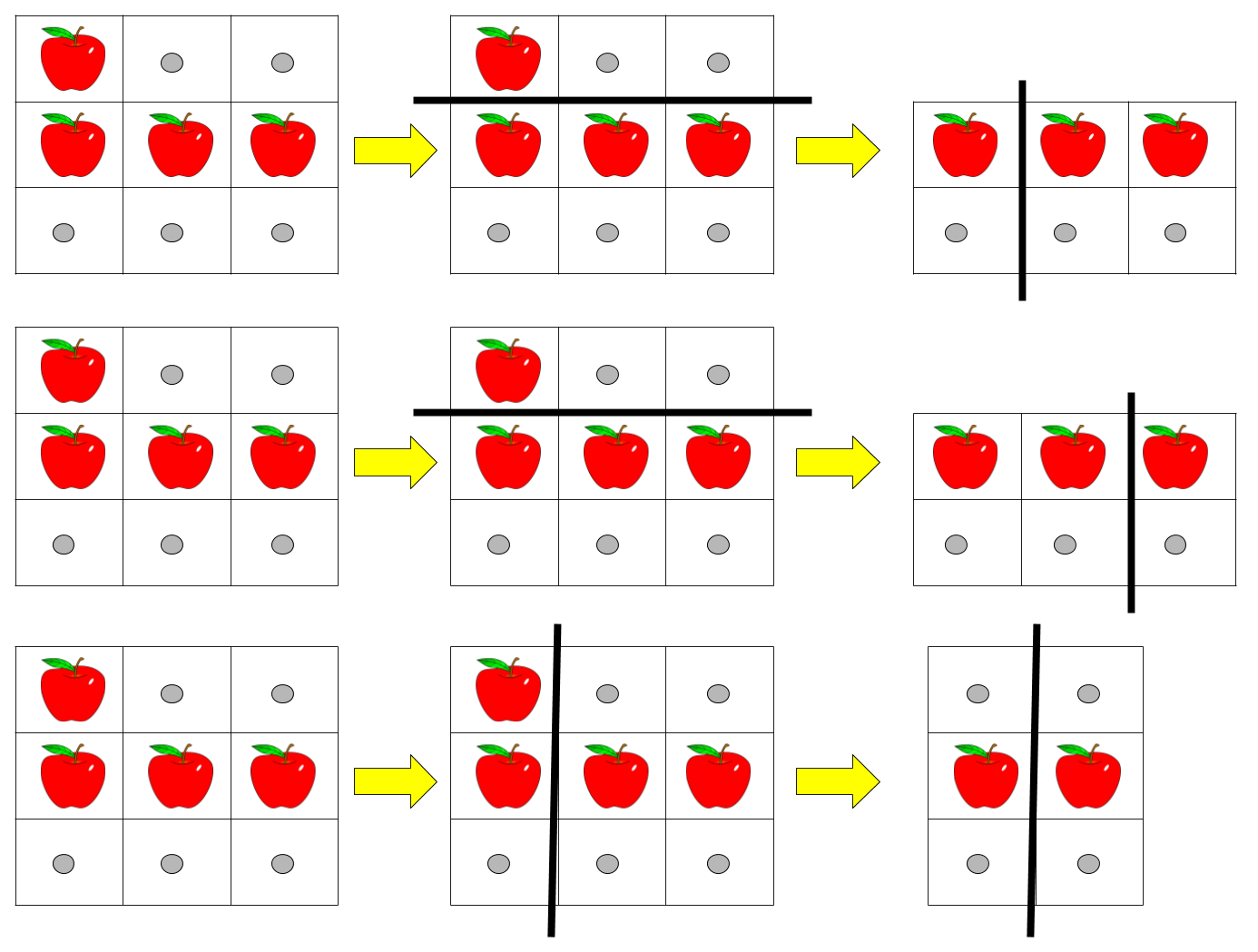
输入：pizza = ["A..","AAA","..."], k = 3
输出：3
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

输入：pizza = ["A..","AA.","..."], k = 3
输出：1

示例 3：

输入：pizza = ["A..","A..","..."], k = 1
输出：1

• 1 <= rows, cols <= 50
• rows == pizza.length
• cols == pizza[i].length
• 1 <= k <= 10
• pizza 只包含字符 'A' 和 '.' 。

思路：

本题是统计切割方案数，一看就是使用dp，怎么来思考呢？

首先我们考虑存在的状态数：

毫无疑问，披萨被切成k块肯定是状态之一。

而如何表示当前剩余部分的披萨呢？题中说把左边和上边给一个人，可以知道，右下部分总是会剩余下来。

所以可以记录左上角的位置来表示剩余的披萨。

因此一个三维数组可以做为dp数组：dp[i][j][k]

i,j表示披萨剩余部分的左上角,k表示当前披萨被切成k块

初始状态显而易见，由于只有一块，没有切，左上角为(0,0)，所以dp[0][0][1]=1

状态转移

知道初始状态后，我们就要开始进行状态转移了~

首先让我们来考虑怎么从一块变成两块

披萨：
A..
AAA
...

由于我们知道可以水平切和垂直切，左上角为(i,j)，一刀切下去，可以从k变成k+1

因此，我们可以穷举每个状态水平切和垂直切的所有切法，来得到k+1的状态。

因为每切一次得到的剩余披萨左上角都不同，所以不会出现重复。

首先水平切：

左上角为(0,0),k=1
A..                                 A..
+++                                 AAA
AAA                                 +++
...                                 ...
剩余部分：左上角为(1,0),k=2           剩余部分：左上角为(2,0),k=2 (不合理)

有这两种切法，很清楚看出来，第二种切法是不可以的，因为下面那一部分不存在A，不符合题意。

如何判断剩余和切出来的披萨存不存在A，我们先记下这个问题，后面会提到。

所以可以得到水平切的状态转移方程：

记原来的左上角为(i,j),新的左上角为(x,y)
if(两部分都存在A){
dp[x][y][k+1]+=dp[i][j][k]
}

垂直切是和水平切一样的，就不说了。

解决存在A的问题

我们如何判断切开后的两块披萨是否存在A呢？

方法1：直接暴力求解，我不知道会不会超时，我没有试，有兴趣可以写一下。

方法2：利用数学知识，计算出来对应披萨块中A的数量，假如数量大于0，则存在A

方法3：别的方法，假如有人愿意分享更简单的，可以在评论分享，大家一起进步

我使用方法2，所以就写一下方法2：

用数组num[i][j]表示以(0,0)为左上角，(i,j)为右下角的披萨块中包含的A数量

上例中：
num:
1 1 1
2 3 4
2 3 4

怎么计算num数组使用简单的dp和数学知识就可以了，这里就不再赘述。

通过num数组和获得披萨块的左上角和右下角就可以轻易地算出A的个数：

这个大家肯定都会，就举个例子吧，就是简单的数学关系：
例：计算以(1,0)为左上角，(2,2)为右下角的披萨块A数目：
num[2][2]-num[0][2]-num[2][-1]+num[0][-1];
下标中出现-1的num值都用0代替：所以为4-1-0-0=3

看不懂的可以直接看代码如何计算A数目，一看就明白了

#define ll long long int

class Solution {
public:

    const ll mod=1e9+7;
    int ways(vector<string>& pizza, int k) {
        int row=pizza.size(),col=pizza[0].length();
        //计算num
        vector<vector<int>> num(row,vector<int>(col,0));
        if(pizza[0][0]=='A') num[0][0]=1;
        for(int i=1;i<row;i++) num[i][0]=num[i-1][0]+(pizza[i][0]=='A');
        for(int i=1;i<col;i++) num[0][i]=num[0][i-1]+(pizza[0][i]=='A');
        for(int i=1;i<row;i++) for(int j=1;j<col;j++)
                num[i][j]=num[i-1][j]+num[i][j-1]-num[i-1][j-1]+(pizza[i][j]=='A');

        //初始化dp
        vector<vector<vector<ll>>> dp(row,vector<vector<ll>>(col,vector<ll>(k+1,0)));
        dp[0][0][1]=1;

        //从k=2开始填充
        for(int x=2;x<=k;x++){
            for(int i=0;i<row;i++){
                for(int j=0;j<col;j++){
                    //dp为0代表不存在这种情况
                    if(dp[i][j][x-1]==0)
                        continue;
                    //穷举水平切
                    for(int z=i+1;z<row;z++){
                        if(hasA(num,i,j,z-1,col-1) && hasA(num,z,j,row-1,col-1)){
                            dp[z][j][x]+=dp[i][j][x-1];
                            dp[z][j][x]%=mod;
                        }
                    }
                    //穷举垂直切
                    for(int z=j+1;z<col;z++){
                        if(hasA(num,i,j,row-1,z-1) && hasA(num,i,z,row-1,col-1)){
                            dp[i][z][x]+=dp[i][j][x-1];
                            dp[i][z][x]%=mod;
                        }
                    }
                }
            }
        }

        //计算答案
        ll ans=0;
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                ans+=dp[i][j][k];
            }
            ans%=mod;
        }
        return ans;
    }

    //计算存在A吗
    bool hasA(vector<vector<int>>& num,int sr,int sc,int er,int ec){
        int num1=0,num2=0,num3=0,res;
        if(sr!=0 && sc!=0) num1=num[sr-1][sc-1];
        if(sr!=0) num2=num[sr-1][ec];
        if(sc!=0) num3=num[er][sc-1];
        return num[er][ec]-num2-num3+num1>0;
    }
};