@codeforces - 549E@ Sasha Circle

@description@
@solution@
@accepted code@
@details@

@description@

给定两个点集 M 与 S，求是否存在一个圆能够分割两个点集。

@solution@

不妨考虑圆内是 M，圆外是 S 的情况。反过来同理。

如果 M 只有一个点，显然有解；否则至少可以让分割圆经过 M 的凸包上的某两个点。

一个暴力做法是枚举这两个点 x, y，则其他点会对分割圆的位置产生限制。可以用 $\vec{xy}$ 所对圆周角大小来描述这一限制。

因为 $\cot$ 在 $(0, \pi)$ 中是单调递减的，且 $\cot(x) = \cot(x - π)$。为了方便，我们不妨用 $\cot(\angle xoy)$ 的大小来描述 $\vec{xy}$ 所对圆周角。

算 $\cot$ 时直接用点乘除以叉乘即可。

具体而言，如果 o 是 M 中的点：

当 $\angle xoy < \pi$ 时正确的圆周角 $\alpha < \angle xoy$，即 $\cot(\alpha) > \cot(\angle xoy)$。

当 $\angle xoy > \pi$ 时正确的圆周角 $\alpha > \angle xoy - \pi$，即 $\cot(\alpha) < \cot(\angle xoy)$。

S 中的点反过来即可。还要注意判三点共线。

当然暴力肯定过不了。我们不妨再分析一下。

我们可以枚举圆经过的点，然后进行圆反演，之后就是直线分割点集问题。然而这个做法带个 log，过不了。

不妨考虑另一种变换：我们将二维平面的点 (x, y) 变换到三维曲面中的点 (x, y, x^2 + y^2)。

此时联立三维空间中的平面解析式 ax + by + cz = 1 与曲面解析式 z = x^2 + y^2，可以得到 ax + by + c(x^2 + y^2) = 1，也就是平面内圆的解析式。

也就是说，任意平面与这个曲面的交投射在 xy 平面上都是圆。我们就把平面圆分割点集转化成了立体的平面分割点集，平面上方的在圆外，平面下方的在圆内。

。。。看上去好像并没有变简单，我们继续分析。

注意到 M 集合只有上凸包有用，而曲面 z = x^2 + y^2 是下凸的，因此 M 集合中只有平面凸包上点有用（附一张官方题解图）。

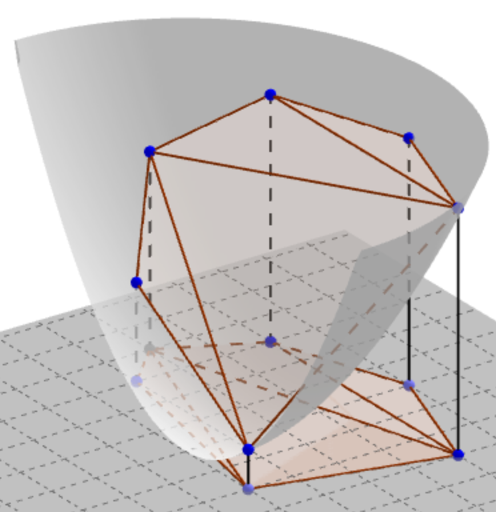
可以调整分割平面使得平面经过 M 的立体上凸包的棱。也就是说，我们可以对立体上凸包中每一条棱做一遍最初的暴力。

然而直接求三维凸包依然很头疼。注意到立体上凸包投射到 xy 平面上实际上形成了一个平面凸包的三角剖分，只需要求出这个三角剖分即可。

这个三角剖分有什么性质？每一个三角形对应了立体凸包的一个面，而立体凸包的面的投影是一个圆。

也就是说，每一个三角形的外接圆都是包含整个凸包的极大圆。

我们可以通过分治寻找这个三角剖分，找极大圆的流程一样使用 cot，和暴力检验做法差不多。

由于值域为 C 的整点凸包点数为 $O(C^{\frac{2}{3}})$（我也不会证啊），所以求剖分的复杂度为 $O(n^{\frac{4}{3}})$，求完过后做暴力的总复杂度 $O(n^{\frac{5}{3}})$。

@accepted code@

#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define double long double
const int MAXN = 10000;
const double INF = 1E18;
const double EPS = 1E-10;
int dcmp(double x) {
	return fabs(x) < EPS ? 0 : (x < 0 ? -1 : 1);
}
struct point{
	int x, y; point() {}
	point(int _x, int _y) : x(_x), y(_y) {}
	friend point operator + (point a, point b) {return point(a.x + b.x, a.y + b.y);}
	friend point operator - (point a, point b) {return point(a.x - b.x, a.y - b.y);}
	friend int operator * (point a, point b) {return a.x*b.x + a.y*b.y;}
	friend int operator ^ (point a, point b) {return a.x*b.y - b.x*a.y;}
	friend bool operator < (point a, point b) {
		return (a.x == b.x ? a.y < b.y : a.x < b.x);
	}
};
double cot(point p, point q) {return 1.0 * (p * q) / (p ^ q);}
point a[MAXN + 5], b[MAXN + 5]; int n, m;
bool get(point p1, point p2) {
	double l = -INF, r = INF;
	for(int i=1;i<=n;i++) {
		if( ((p1 - a[i]) ^ (p2 - a[i])) == 0 ) {
			if( ((p1 - a[i]) * (p2 - a[i])) > 0 ) return false;
		}
		else {
			double k = cot(p1 - a[i], p2 - a[i]);
			if( ((p1 - a[i]) ^ (p2 - a[i])) > 0 )
				l = max(l, k);
			else r = min(r, k);
		}
	}
	for(int i=1;i<=m;i++) {
		if( ((p1 - b[i]) ^ (p2 - b[i])) == 0 ) {
			if( ((p1 - b[i]) * (p2 - b[i])) <= 0 ) return false;
		}
		else {
			double k = cot(p1 - b[i], p2 - b[i]);
			if( ((p1 - b[i]) ^ (p2 - b[i])) > 0 )
				r = min(r, k);
			else l = max(l, k);
		}
	}
	return dcmp(r - l) > 0;
}
bool solve(int l, int r) {
	if( get(a[l], a[r]) ) return true;
	if( l + 1 == r ) return false;
	int p = l + 1;
	for(int i=l+1;i<=r-1;i++)
		if( dcmp(cot(a[r] - a[i], a[l] - a[i]) - cot(a[r] - a[p], a[l] - a[p])) < 0 )
			p = i;
	return solve(l, p) || solve(p, r);
}
bool check(point *p, int _n, point *q, int _m) {
	n = 0; int o = 1;
	for(int i=1;i<=_n;i++) {
		while( n > o && ((a[n - 1] - a[n]) ^ (p[i] - a[n])) <= 0 )
			n--;
		a[++n] = p[i];
	}
	o = n;
	for(int i=_n-1;i>=1;i--) {
		while( n > o && ((a[n - 1] - a[n]) ^ (p[i] - a[n])) <= 0 )
			n--;
		a[++n] = p[i];
	}
	n--;
	for(int i=1;i<=_m;i++) b[i] = q[i]; m = _m;
	return solve(1, n);
}
point M[MAXN + 5], S[MAXN + 5];
int main() {
	int _n, _m; scanf("%d%d", &_n, &_m);
	for(int i=1;i<=_n;i++) scanf("%d%d", &M[i].x, &M[i].y);
	for(int i=1;i<=_m;i++) scanf("%d%d", &S[i].x, &S[i].y);
	sort(M + 1, M + _n + 1), sort(S + 1, S + _m + 1);
	puts(_n == 1 || _m == 1 || check(M, _n, S, _m) || check(S, _m, M, _n) ? "YES" : "NO");
}

@details@

集训队作业开门自闭题.jpg。因为种种原因还是决定还是把这道题补了。

调计算几何题调得我想吐，一开始无穷大设小了 WA 了几次，然后 cot 比较写反了又 WA 了几次。顺便去学了个别人的凸包写法。

因为这个凸包不是斜率优化的凸包，所以可以直接叉乘判是否 < 180°。