等效燃油消耗ECMS与庞德里亚金最小值原理PMP中协同状态的关系

　　今儿阅读了一篇文献——《车联网环境下并联混合动力客车控制策略优化研究》，是北理的博士所写的，内容比较翔实。主要是里面的关于ECMS和庞德里亚金最小值原理（PMP）的关系推导很让人印象深刻，故打算把这个过程捋一下。需要说明的是本文同时也参考了文献【2】的第五章主讲PMP的证明过程。

　　文献【1】首先是将汉密尔顿函数用于能量管理策略，表示的结果就如下式4.49所示，λ(t)是协同状态，而根据PMP（庞德里亚金最小值）原理，协同状态的动态方程可以由公式4.50表示

　　

　　

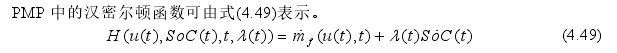
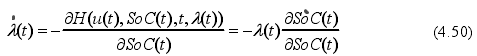
　　在文献【2】的第55页，是这样去描述这个过程，公式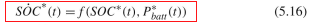

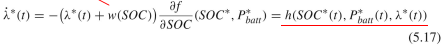
和上面文献【1】的公式是表达一样的意思，而公式5.17中的w(SOC)则是类似于惩罚函数一样的东西，主要是判断取值是否超出边界，在文献【2】中w(SOC)的公式如下。 而公式5.16和5.17之所以要在状态量上加一个*号，就是表达这是最优的取值。

　　根据电池SOC在文献【1】中的计算公式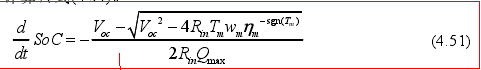，然后作者认为普通混动汽车电池SOC在较小的范围内变动，所以电池开路电压Voc和内阻Rin是常数，与电池SOC无关，所以就推导出公式4.52如下，然后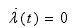，所以协同状态λ就是一个常数。

　　在文献【2】中是如何推导这个过程的呢？作者把公式5.16和5.17进行变化，利用公式3.4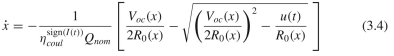，公式3.4中的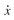其实就是dSOC/dt，也就是和文献【1】中的4.51一样。最后得到的结果就如公式5.21所示，。其中的推导过程其实如下，紧接着文献【2】里面说开路电压和内阻相对于SOC的变化可以忽略不计，于是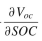和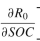都是0，那么公式5.21也变成0了，所以协同状态λ就是一个常数。总的来看，推导过程几乎一致，唯一的区别是文献【2】更准确的说明了Voc和内阻R是相对于SOC的倒数为0，而不是一直是个常数不变。

　　基于以上的推导过程，文献【1】最终得到的汉密尔顿函数的另一种形式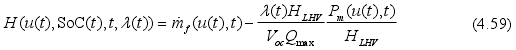，，然后再和ECMS的表达式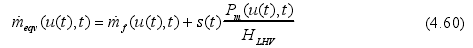进行比较，就可以发现等效因子和协同状态λ之间的关系：

要记住上面的推导结论，协同状态λ就是一个常数，但是等效因子s不一定是一个常数，因为开路电压和内阻其实是随时间变化的，电池如果老化了，容量值也会发生变化。

　　这里必须得说明一下，上面文献【1】中的公式4.59，可以把它稍微变形，因为I=P_m/V_oc，而电池SOC的变化 dSOC/dt = I/Q_nom，又因为汉密尔顿函数和ECMS等效起来，所以其实可以把ECMS的形式写成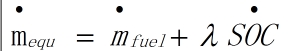，这样的话可以把电机的功率值替换成电池SOC，实现起来更为直观。

参考文献：

【1】《车联网环境下并联混合动力客车控制策略优化研究》

【2】Hybrid Electric Vehicles Energy Management Strategies，Chapter 5