POJ 3249 Test for Job(拓扑排序+dp优化空间)

Description

Mr.Dog was fired by his company. In order to support his family, he must find a new job as soon as possible. Nowadays, It's hard to have a job, since there are swelling numbers of the unemployed. So some companies often use hard tests for their recruitment.

The test is like this: starting from a source-city, you may pass through some directed roads to reach another city. Each time you reach a city, you can earn some profit or pay some fee, Let this process continue until you reach a target-city. The boss will compute the expense you spent for your trip and the profit you have just obtained. Finally, he will decide whether you can be hired.

In order to get the job, Mr.Dog managed to obtain the knowledge of the net profit V_i of all cities he may reach (a negative V_i indicates that money is spent rather than gained) and the connection between cities. A city with no roads leading to it is a source-city and a city with no roads leading to other cities is a target-city. The mission of Mr.Dog is to start from a source-city and choose a route leading to a target-city through which he can get the maximum profit.

Input

The input file includes several test cases. 
The first line of each test case contains 2 integers n and m(1 ≤ n ≤ 100000, 0 ≤ m ≤ 1000000) indicating the number of cities and roads. 
The next n lines each contain a single integer. The ith line describes the net profit of the city i, V_i (0 ≤ |V_i| ≤ 20000) 
The next m lines each contain two integers x, y indicating that there is a road leads from city x to city y. It is guaranteed that each road appears exactly once, and there is no way to return to a previous city. 

Output

The output file contains one line for each test cases, in which contains an integer indicating the maximum profit Dog is able to obtain (or the minimum expenditure to spend)

Sample Input

6 5
1
2
2
3
3
4
1 2
1 3
2 4
3 4
5 6

Sample Output

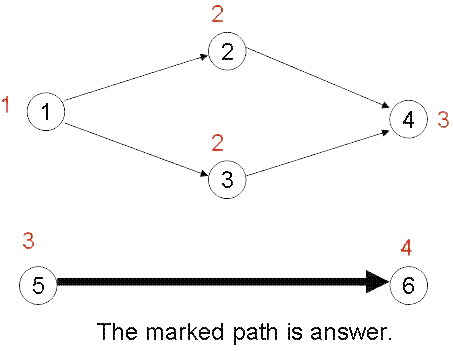
7

Hint

题意：给出n个点的权值和m条路径, 问一条路的最大权值是多少.

思路：原本思路是BFS枚举..然而MLE了，那么只能用dp来优化空间了。。两者都是枚举所有情况，前者将每次情况存入队列时容易因为图稠密而MLE；后者仅不断更新dp数组，在空间上节省了很多。

 #include "iostream"

 #include "cstdio"

 #include "cstring"

 #include "algorithm"

 #include "queue"

 #include "stack"

 #include "cmath"

 #include "utility"

 #include "map"

 #include "set"

 #include "vector"

 #include "list"

 #include "string"

 using namespace std;

 typedef long long ll;

 const int MOD = 1e9 + ;

 const int INF = 0x3f3f3f3f;

 const int MAXN = 1e5 + ;

 int n, m, num;

 int cost[MAXN], in[MAXN], out[MAXN], head[MAXN], dp[MAXN];

 bool vis[MAXN];

 struct node

 {

     /* data */

     int fr, to, nxt;

 }e[MAXN * ];

 void add(int x, int y)

 {

     e[num].fr = x;

     e[num].to = y;

     e[num].nxt = head[x];

     head[x] = num++;

 }

 void toposort()

 {

     int cnt = ;

     while(cnt < n) {

         for(int i = ; i <= n; ++i)

             if(in[i] ==  && !vis[i]) {

                 vis[i] = true;

                 cnt++;

                 for(int j = head[i]; j != -; j = e[j].nxt) {

                     int x = e[j].to;

                     in[x]--;

                     if(dp[i] + cost[x] > dp[x]) dp[x] = dp[i] + cost[x];

                 }

             }

     }

 }

 int main(int argc, char const *argv[])

 {

     while(scanf("%d%d", &n, &m) != EOF) {

         memset(in, , sizeof(in));

         memset(out, , sizeof(out));

         memset(head, -, sizeof(head));

         memset(vis, false, sizeof(vis));

         num = ;

         for(int i = ; i <= n; ++i)

             scanf("%d", &cost[i]);

         for(int i = ; i <= m; ++i) {

             int x, y;

             scanf("%d%d", &x, &y);

             add(x, y);

             in[y]++;

             out[x]++;

         }

         for(int i = ; i <= n; ++i)

             if(in[i] == ) dp[i] = cost[i];

             else dp[i] = -INF;

         toposort();

         int ans = -INF;

         for(int i = ; i <= n; ++i)

             if(out[i] ==  && dp[i] > ans) ans = dp[i];

         printf("%d\n", ans);

     }

     return ;

 }

代码转自（https://blog.csdn.net/gkhack/article/details/50223357）