Food HDU - 4292 网络流 拆点建图

http://acm.hdu.edu.cn/showproblem.php?pid=4292

给一些人想要的食物和饮料,和你拥有的数量,问最多多少人可以同时获得一份食物和一份饮料

写的时候一共用了2种拆点建图的方法...

1.

　　起点连接饮料和食物,容量为拥有的数量

　　每个人被拆成三个点,$a,b,c$  $a$被想要的食物连接,$b$被想要的饮料连接,$c$被$a,b$连接,容量均为1

　　然后$c$点连接汇点,容量为2,最后遍历所有静态链表节点,对于所有指向汇点的边,如果剩余容量为0,则答案++

　　

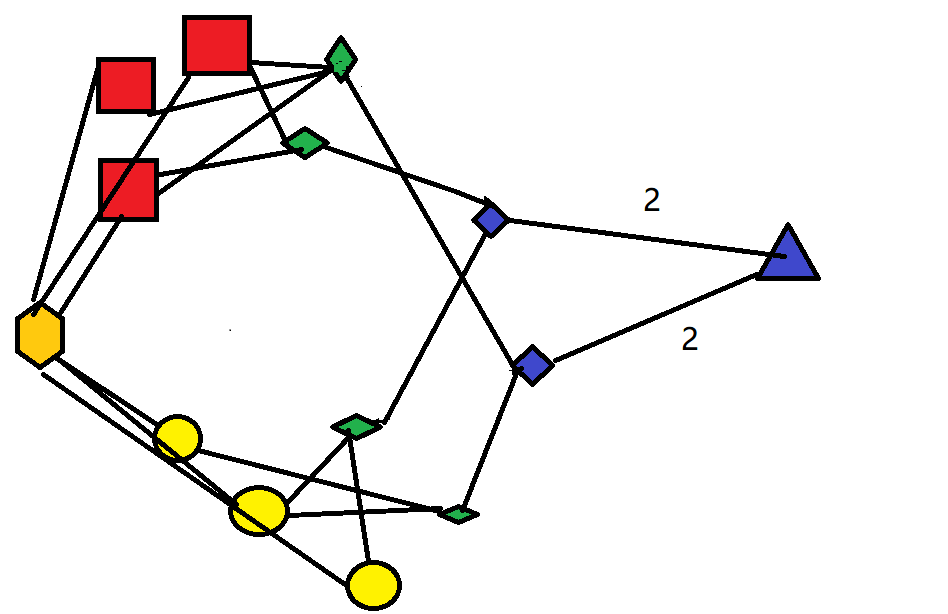
　　然而错了,有的点会为了更大的流量而不填满$C-T$的边...会少算很多

2.

　　汇点连接食物,容量为拥有量,把每个人拆成2个点$a,b$,$a$被食物连接,$a$再连接$b$,$b$再连接饮料,容量均为1,最终饮料连接汇点容量为拥有量,

#include <bits/stdc++.h>
#define ll long long
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define pp pair<int,int>
#define rep(ii,a,b) for(int ii=a;ii<=b;ii++)
#define	per(ii,a,b) for(int ii=a;ii>=b;ii--)
#define show(x) cout<<#x<<"="<<x<<endl
#define show2(x,y) cout<<#x<<"="<<x<<" "<<#y<<"="<<y<<endl
#define show3(x,y,z) cout<<#x<<"="<<x<<" "<<#y<<"="<<y<<" "<<#z<<"="<<z<<endl
#define showa(a,b) cout<<#a<<'['<<b<<"]="<<b[a]<<endl
using namespace std;
const int maxn=1e4+10;
const int maxm=1e6+10;
const int INF=0x3f3f3f3f;
int casn,n,m,k;
struct node {int to;int cap;int next;}e[maxm];
int ss,tt,head[maxn],nume,dis[maxn];
inline void addx(int a,int b,int c){
	e[++nume]=(node){b,c,head[a]};
	head[a]=nume;
}
inline void add(int a,int b,int c){
	addx(a,b,c);addx(b,a,0);
}
bool bfs(int s=ss,int t=tt){
	int top=0,end=1;
	int q[maxn];
	q[0]=s;
//	for(int i=0;i<=t;i++) dis[i]=0;
	memset(dis,0,sizeof dis);
	dis[s]=1;
	while(top!=end){
		int now=q[top++];top%=maxn;
		for(int i=head[now];i;i=e[i].next){
			int to=e[i].to;
			if(!dis[to]&&e[i].cap){
				dis[to]=dis[now]+1;
				if(to==t)break;
				q[end++]=to;end%=maxn;
			}
		}
	}
	return dis[t];
}
int dfs(int now=ss,int last=INF){
	if(now==tt)return last;
	int flow=0,det;
	for(int i=head[now];i;i=e[i].next){
		int to=e[i].to;
		if(e[i].cap&&dis[to]==dis[now]+1){
			det=dfs(to,min(last-flow,e[i].cap));
			flow+=det;
			e[i].cap-=det;
			e[i^1].cap+=det;
			if(flow==last) return last;
		}
	}
	dis[now]=-1;
	return flow;
}
int a,b,c;
char ch[maxn];

int main(){
//#define test
#ifdef test
	freopen("in.txt","r",stdin);freopen("out.txt","w",stdout);
#endif
	int d,f;
	while(~scanf("%d%d%d",&n,&f,&d)){
		memset(head,0,sizeof head);
		nume=1;
		ss=0,tt=d+f+3*n+1;
		rep(i,1,f) {
			scanf("%d ",&a);
			add(ss,i,a);
		}
		rep(i,1,d){
			scanf("%d ",&a);
			add(i+f+2*n,tt,a);
		}
		rep(i,1,n){
			scanf("%s",ch);
			rep(j,1,f){
				if(ch[j-1]=='Y') add(j,i+f,1);
			}
		}
		rep(i,1,n){
			scanf("%s",ch);
			rep(j,1,d){
				if(ch[j-1]=='Y') add(i+f+n,j+f+2*n,1);
			}
			add(i+f,i+f+n,1);
		}
		int ans=0;
		while(bfs()){ans+=dfs();}
		printf("%d\n",ans);
	}

#ifdef test
	fclose(stdin);fclose(stdout);system("out.txt");
#endif
	return 0;
}