hdu 2476"String painter"(区间DP)

传送门

https://www.cnblogs.com/violet-acmer/p/9852294.html

题意：

　　给定字符串A,B，每次操作可以将字符串A中区间[ i , j ]的字符变为ch，问最少需要多少次操作可以使 A == B。

题解：

　　这道题，卡了我好久好久，这期间也尝试用了一些骚操作，然而并没有什么卵用，无奈之举，百度找了巨巨的博客看。

　　看了三四篇博客，在经过自己的纠结，终于弄懂了。

　　首先，这道题需要经过两次DP：

　　① : 第一次是求出将空字符串 S 变为 B 所需的最少操作，定义dp[ i ][ j ] : S[ i,......,j ] == B[ i,......,j ] 所需的最少操作。

　　② : dp[ ][ ] 求出后，然后根据巨巨的解释就是“A串中的字符与B字符串对应的位置可能存在相同的情况，所以又存在减少次数的可能，这里又会再次用DP计算”

　　最难理解的便是dp[ ][ ]求解的过程。

　　状态转移方程如下：

 );
 mem(dp,);
 ;i <= lenA;++i)
     dp[i][i]=;//S[i]变为B[i]需要一次操作，不要忘了S[]为空字符串
 ;len <= lenA;++len)//区间长度
 {
     ;i+len- <= lenA;++i)//求解dp[i,j]
     {
         ;
         //初始化dp[i][j]
         //dp[i][j]=( S[i+1,j]变为B[i+1,j]所需的最少操作dp[i+1][j] )+( S[i]变为B[i]需要一次操作 )
         dp[i][j]=dp[i+][j]+;
         ;k <= j;++k)
             if(B[i] == B[k])
                 dp[i][j]=min(dp[i][j],dp[i+][k-]+dp[k][j]);
     }
 }

　　我的理解：

　　　　①如果B[ i+1,......,j ]中的字符都不等于 B[ i ]，那么 dp[ i ][ j ]=dp[ i+1 ][ j ]+1 ;  这也就对应了初始化dp[ i ][ j ]语句，却不会执行for( )循环中的 if 语句。

　　　　②如果B[ i+1,......,j ]含有字符等于 B[ i ]，如图所示

　　　　　　

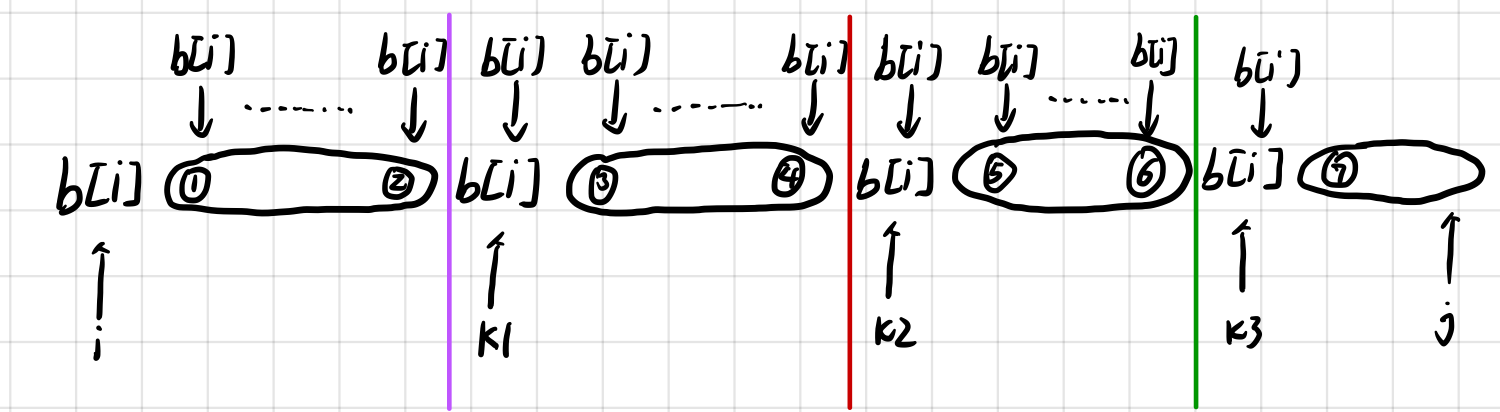
　　　　　　当 k = k1 时，状态转移方程  dp[ i ][ j ]=min( dp[ i ][ j ] , dp[ i+1 ][ k-1 ]+dp[ k ][ j ] ); 还是比较好理解的，就是在将 S[ k1 ] 变为 B[ i ]的时候一次性也将

　　　　S[ ①,......,② ] 变成 B[ i ]，因为 B[ k1 ] 是第一个等于 B[ i ] 的，所以 [ ①,......,② ]区间并没有等于 B[ i ] 的字符，那么，将 S[ ①,......,② ] 变为"B[ i ]"或"为空"

　　　　对之前所求的 dp[ ①,......,② ] 无影响。

　　　　　　当 k = k2 时，为什么还是用 dp[ i+1 ][ k-1 ] 呢？

　　　　　　思路依旧是 k = k1 时的思路，“在将 S[ k2 ] 变为 B[ i ]的时候一次性也将 S[ ①,......,④ ] 变成 B[ i ]”，那么，该如何求解 dp[ ①,......,④ ]呢？

　　　　　　根据状态转移方程 dp[ i ][ j ] = min( dp[ i ][ j ] , dp[ i ][ k-1]+dp[ k ][ j ] ),所以说 整体的dp ≤ 部分的dp，即dp[ i ][ j ] ≤ dp[ i ][ k-1 ]+dp[ k ][ j ]。

　　　　　　当 k = k3,k4,..... 时同理。

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 #define mem(a,b) memset(a,b,sizeof(a))
 +;

 char A[maxn],B[maxn];
 int dp[maxn][maxn];
 int f[maxn];

 int Solve()
 {
     );
     mem(dp,);
     ;i <= lenA;++i)
         dp[i][i]=;//S[i]变为B[i]需要一次操作，不要忘了S[]为空字符串
     ;len <= lenA;++len)//区间长度
     {
         ;i+len- <= lenA;++i)//求解dp[i,j]
         {
             ;
             dp[i][j]=dp[i+][j]+;
             ;k <= j;++k)
                 if(B[i] == B[k])
                     dp[i][j]=min(dp[i][j],dp[i+][k-]+dp[k][j]);
         }
     }
     ;i <= lenA;++i)
     {
         f[i]=dp[][i];
         if(A[i] == B[i])
             f[i]=f[i-];
         else
         {
             //如果A[i] != B[i]
             //那么，从[1,i]之间任意位置断开成[1,k]和[k+1,j]，求两部分区间的最小值
             ;k <= i;++k)
                 f[i]=min(f[i],f[k]+dp[k+][i]);
         }
     }
     return f[lenA];
 }
 int main()
 {
     ,B+))
     {
         printf("%d\n",Solve());
     }
     ;
 }

　　　　其实，感觉对 k > k1 时的理解还是有点牵强，先放放吧，过一段时间在回头理解一下，说不定就顿悟了呢。

　　　　还望有理解的巨巨留言相告，定感激不尽