BZOJ1101: [POI2007]Zap(莫比乌斯反演)

1101: [POI2007]Zap

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 2951  Solved: 1293
[Submit][Status][Discuss]

Description

　　FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a
，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

Input

　　第一行包含一个正整数n，表示一共有n组询问。（1<=n<= 50000）接下来n行，每行表示一个询问，每行三个
正整数，分别为a,b,d。（1<=d<=a,b<=50000）

Output

　　对于每组询问，输出到输出文件zap.out一个正整数，表示满足条件的整数对数。

Sample Input

2
4 5 2
6 4 3

Sample Output

3
2
//对于第一组询问，满足条件的整数对有(2,2)，（2,4），（4，2）。对于第二组询问，满足条件的整数对有（
6,3），（3,3）。

HINT

 

Source

莫比乌斯反演裸题

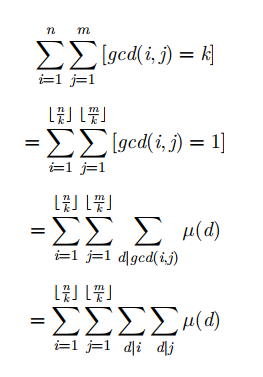
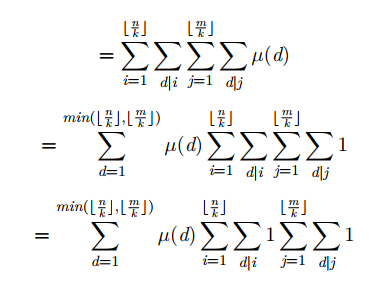
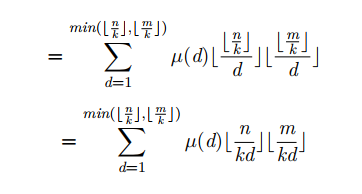
$\frac{n}{k}$只有$sqrt(n)$个取值

所以可以用分块优化

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN=1e6+;
inline int read()
{
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int N;
int vis[MAXN];
long long prime[MAXN],mu[MAXN],tot=;
void GetMu()
{
    vis[]=;mu[]=;
    for(int i=;i<=N;i++)
    {
        if(!vis[i]) prime[++tot]=i,mu[i]=-;
        for(int j=;j<=tot&&i*prime[j]<=N;j++)
        {
            vis[i*prime[j]]=;
            if(i%prime[j]==) {mu[i*prime[j]]=;break;}
            else mu[i*prime[j]]=-mu[i];
        }
    }
    for(int i=;i<=N;i++) mu[i]+=mu[i-];
}
main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    #endif
    N=1e5;
    GetMu();
    int QWQ=read();
    while(QWQ--)
    {
        int n=read(),m=read(),k=read();
        long long ans=;
        int limit=min(n/k,m/k);
        int nxt=;
        for(int i=;i<=limit;i=nxt+)
            nxt=min(n/(n/i),m/(m/i)),
            ans+=(mu[nxt]-mu[i-])*((n/k)/i)*((m/k)/i);
        printf("%lld\n",ans);
    }
    return ;
}