c/c++连通图的遍历(深度遍历/广度遍历)

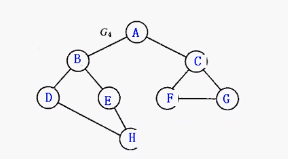
连通图的遍历(深度遍历/广度遍历)

概念：图中的所有节点都要遍历到，并且只能遍历一次。

• 深度遍历
• 广度遍历

深度遍历

概念：从一个给定的顶点开始，找到一条边，沿着这条边一直遍历。

广度遍历

概念：从一个给定的顶点开始，找到这个顶点下的所有子顶点后，再找下一层的子顶点。

深度遍历的实现思路

1，创建一个bool数组，用来识别哪个顶点已经被遍历过了。

2，递归

3，递归找给定顶点是否有下一个顶点（方法：get_first_neighbor），都找完后，

4，再递归找给定顶点之后的在3处找到的顶点后的下一个顶点（方法：get_next_neighbor）

光度遍历的实现思路

1，用队列实现，先入队给定顶点

2，出队

3，入队：与在2处出队的顶点有相连的顶点

代码

graph_link.h

#ifndef __graph_link__
#define __graph_link__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>
#include <stdbool.h>

#define default_vertex_size 10
#define T char

//边的结构
typedef struct Edge{
  //顶点的下标
  int idx;
  //指向下一个边的指针
  struct Edge* link;
}Edge;

//顶点的结构
typedef struct Vertex{
  //顶点的值
  T data;
  //边
  Edge* adj;
}Vertex;

//图的结构
typedef struct GraphLink{
  int MaxVertices;
  int NumVertices;
  int NumEdges;

  Vertex* nodeTable;
}GraphLink;

//初始化图
void init_graph_link(GraphLink* g);
//显示图
void show_graph_link(GraphLink* g);
//插入顶点
void insert_vertex(GraphLink* g, T v);
//插入边尾插
void insert_edge_tail(GraphLink* g, T v1, T v2);
//插入边头插
void insert_edge_head(GraphLink* g, T v1, T v2);
//删除边
void remove_edge(GraphLink* g, T v1, T v2);
//删除顶点
void remove_vertex(GraphLink* g, T v);
//销毁图
void destroy_graph_link(GraphLink* g);
//取得指定顶点的第一个后序顶点
int get_first_neighbor(GraphLink* g, T v);
//取得指定顶点v1的临街顶点v2的第一个后序顶点
int get_next_neighbor(GraphLink* g, T v1, T v2);

//深度遍历
void dfs_graph(GraphLink* g, T v);
//取得顶点的data值
T getVertexValue(GraphLink* g, int i);
//广度遍历
void cfs_graph(GraphLink* g, T v);

#endif

graph_link.c

#include "graph_link.h"
#include "nodequeue.h"

//初始化图
void init_graph_link(GraphLink* g){
  g->MaxVertices = default_vertex_size;
  g->NumVertices = g->NumEdges = 0;

  g->nodeTable = (Vertex*)malloc(sizeof(Vertex) * g->MaxVertices);
  assert(NULL != g->nodeTable);
  for(int i = 0; i < g->MaxVertices; ++i){
    g->nodeTable[i].adj = NULL;
  }
}

//显示图
void show_graph_link(GraphLink* g){
  if(NULL == g)return;
  for(int i = 0; i < g->NumVertices; ++i){
    printf("%d %c->", i, g->nodeTable[i].data);
    Edge* p = g->nodeTable[i].adj;
    while(NULL != p){
      printf("%d->", p->idx);
      p = p->link;
    }
    printf(" NULL\n");
  }
}

//插入顶点
void insert_vertex(GraphLink* g, T v){
  if(g->NumVertices >= g->MaxVertices)return;
  g->nodeTable[g->NumVertices++].data = v;
}

//查找顶点的index
int getVertexIndex(GraphLink* g, T v){
  for(int i = 0; i < g->NumVertices; ++i){
    if(v == g->nodeTable[i].data)return i;
  }
  return -1;
}
//插入边(头插）
void insert_edge_head(GraphLink* g, T v1, T v2){
  int p1 = getVertexIndex(g, v1);
  int p2 = getVertexIndex(g, v2);

  if(p1 == -1 || p2 == -1)return;

  Edge* p = (Edge*)malloc(sizeof(Edge));
  p->idx = p2;
  p->link = g->nodeTable[p1].adj;
  g->nodeTable[p1].adj = p;

  p = (Edge*)malloc(sizeof(Edge));
  p->idx = p1;
  p->link = g->nodeTable[p2].adj;
  g->nodeTable[p2].adj = p;
}

//取得指定顶点的第一个后序顶点
int get_first_neighbor(GraphLink* g, T v){
  int i = getVertexIndex(g, v);
  if (-1 == i)return -1;
  Edge* p = g->nodeTable[i].adj;
  if(NULL != p)
    return p->idx;
  else
    return -1;
}

//取得指定顶点v1的临街顶点v2的第一个后序顶点
int get_next_neighbor(GraphLink* g, T ve1, T ve2){
  int v1 = getVertexIndex(g, ve1);
  int v2 = getVertexIndex(g, ve2);
  if(v1 == -1 || v2 == -1)return -1;

  Edge* t = g->nodeTable[v1].adj;
  while(t != NULL && t->idx != v2){
    t = t->link;
  }
  if(NULL != t && t->link != NULL){
    return t->link->idx;
  }
  return -1;
}
//取得顶点的data值
T getVertexValue(GraphLink* g, int i){
  if(i == -1)return 0;
  return g->nodeTable[i].data;
}

//深度遍历
void dfs_graph_v(GraphLink* g, int v, bool* visited){
  printf("%c->", getVertexValue(g,v));
  visited[v] = true;
  //取得相邻顶点的下标
  int w = get_first_neighbor(g, getVertexValue(g, v));
  while(w != -1){
    if(!visited[w]){
      dfs_graph_v(g, w, visited);
    }
    w = get_next_neighbor(g, getVertexValue(g, v), getVertexValue(g,w));
  }
}
void dfs_graph(GraphLink* g, T v){
  int cnt = g->NumVertices;
  bool* visited = (bool*)malloc(sizeof(bool) * cnt);
  assert(NULL != visited);
  for(int i = 0; i < cnt; ++i){
    visited[i] =  false;
  }

  int index = getVertexIndex(g, v);
  dfs_graph_v(g, index, visited);
  free(visited);
}

//广度遍历
void cfs_graph(GraphLink* g, T v){

  //创建一个辅助的bool数组，用来识别哪个顶点已经被遍历过了
  int cnt = g->NumVertices;
  bool* visited = (bool*)malloc(sizeof(bool) * cnt);
  assert(NULL != visited);
  for(int i = 0; i < cnt; ++i){
    visited[i] =  false;
  }

  //创建队列
  NodeQueue q;
  init(&q);
  //入队
  int tar = getVertexIndex(g, v);
  enQueue(&q, tar);

  //队列不为空就执行
  while(length(&q) != 0){
    //取得队列的第一个元素
    int ve = getHead(&q)->data;

    printf("%c->", getVertexValue(g, ve));
    visited[ve] = true;

    //出队
    deQueue(&q);

    Edge* e = g->nodeTable[ve].adj;
    while(NULL != e){
      //如果这个顶点没有被遍历过,入队
      if(!visited[e->idx]){
	visited[e->idx] = true;
	enQueue(&q, e->idx);
      }
      e = e->link;
    }
  }
}

graph_linkmain.c

#include "graph_link.h"

int main(){
  GraphLink gl;
  //初始化图
  init_graph_link(&gl);
  //插入节点
  insert_vertex(&gl, 'A');
  insert_vertex(&gl, 'B');
  insert_vertex(&gl, 'C');
  insert_vertex(&gl, 'D');
  insert_vertex(&gl, 'E');
  insert_vertex(&gl, 'F');
  insert_vertex(&gl, 'G');
  insert_vertex(&gl, 'H');

  insert_edge_head(&gl, 'A', 'B');
  insert_edge_head(&gl, 'A', 'C');
  insert_edge_head(&gl, 'B', 'D');
  insert_edge_head(&gl, 'B', 'E');
  insert_edge_head(&gl, 'C', 'F');
  insert_edge_head(&gl, 'C', 'G');
  insert_edge_head(&gl, 'D', 'H');
  insert_edge_head(&gl, 'E', 'H');
  insert_edge_head(&gl, 'F', 'G');
  //显示图
  show_graph_link(&gl);

  //深度遍历
  dfs_graph(&gl, 'E');
  printf("null\n");

  //广度遍历
  cfs_graph(&gl, 'F');
  printf("null\n");
}

完整代码

编译方法：g++ -g nodequeue.c graph_link.c graph_linkmain.c