插入排序（CSP-J 2021 T2）

题目：（由于题干过长直接上链接：P7910 [CSP-J 2021] 插入排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)） 不是打广告

又有一个新思路：

我们可以再开一个b数组用来记录第i个数排序后的位置并在更改数据（操作一）后维护b数组，使b数组依然适用。

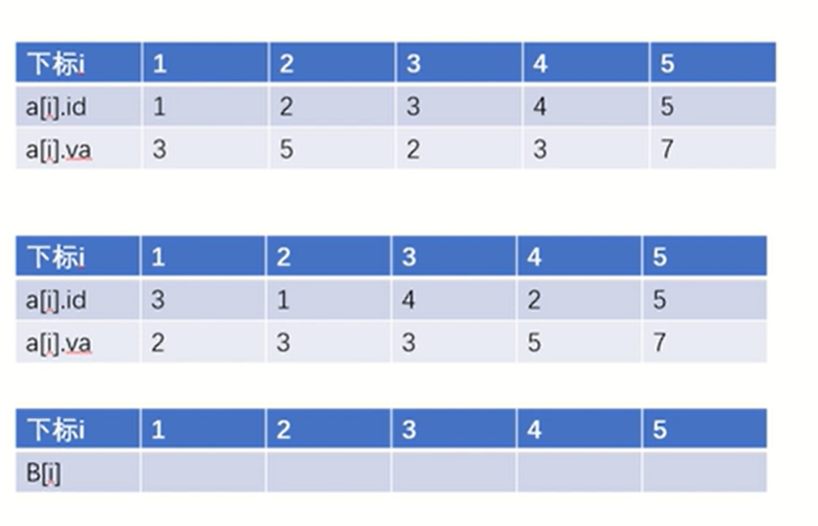
同时还要开一个struct s（用于记录a数组）记录id（输入顺序）和va（输入内容）。

因为要根据输入数据初始化b数组,需要把a数组 sort一遍。因为s是结构体就要自定义cmp，（重点来了！）因为我们要模拟稳定排序所以自定义cmp中除了正常操作（return a.va<b.va;）还有一点，如果在cmp中两个输入的值相等时还要比较这两个值的输入顺序（即id值）,id值小的排在前面，大的排在后面。

通过遍历一遍a数组将b[a[i].id]设为i（意为第a[i].id个数在排序后在i的位置）来初始化b数组。

根据输入判断是哪一种操作 

如果是第一种操作，就是改变a数组，更新b数组。

在a数组中如果替换的数值比原来大就要向右边做一次冒泡，把它放到合适的位置。（如果它不交换了就break掉，能节省不少时间）如果替换的数值比原来的小就向左做冒泡……（强调：如果值一样还要比较id值）

在第一种操作结束之前，我们还要再更新一遍b数组（初始化b数组遍历一遍a数组将b[a[i].id]设为i）。

如果是第二种操作，十分简单输入x，输出b[x]即可（别问我为什么，看了那么多还不明白就重看吧！）。

代码：

#include<bits/stdc++.h>
using namespace std;
struct s{
    int id;
    int va;
}a[8010];
int n,q,b[8010]={0};
int cmp(const s &a,const s &b)
{
    if(a.va!=b.va) return a.va<b.va;
    else return a.id<b.id;
}
int main()
{
#ifdef LOCAL
    freopen("1.in", "r", stdin);
    freopen("1.out", "w", stdout);
#endif
    cin>>n>>q;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i].va;
        a[i].id=i;
    }
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++)
    {
        b[a[i].id]=i;
    }
    while(q--)
    {
        int t;
        scanf("%d",&t);
        if(t==1)
        {
            int x,v;
            scanf("%d%d",&x,&v);
            if(a[b[x]].va<v)
            {
                a[b[x]].va=v;
                for(int i=b[x];i<n;i++)
                {
                    if(a[i].va>a[i+1].va||(a[i].va==a[i+1].va&&a[i].id>a[i+1].id)) swap(a[i],a[i+1]);
                    else break;
                }
            }
            else
            {
                a[b[x]].va=v;
                for(int i=b[x]-1;i>=1;i--)
                {
                    if(a[i].va>a[i+1].va||(a[i].va==a[i+1].va&&a[i].id>a[i+1].id)) swap(a[i],a[i+1]);
                    else break;
                }
            }
            for(int i=1;i<=n;i++)
            {
                b[a[i].id]=i;
            }
        }
        else
        {
            int x;
            scanf("%d",&x);
            printf("%d\n",b[x]);
        }
    }
    return 0;
}

最后，祝大家暑假快乐！