迁移学习《Cluster-Guided Semi-Supervised Domain Adaptation for Imbalanced Medical Image Classification》

论文信息

论文标题：Cluster-Guided Semi-Supervised Domain Adaptation for Imbalanced Medical Image Classification
论文作者：S. Harada, Ryoma Bise, Kengo Araki
论文来源：ArXiv 2 March 2023
论文地址：download 
论文代码：download
视屏讲解：click

1 摘要

　　一种半监督域自适应方法，对医学图像分类任务中常见的类不平衡情况具有鲁棒性。 为了稳健性，提出了一种弱监督聚类流水线来获得高纯度聚类，并在表示学习中利用这些聚类进行域适应。

2 方法

2.1 问题定义

　　Consider that we have a set of  $m^{s}$  labeled source samples,  $\mathcal{D}^{s}=\left\{\left(x_{i}^{s}, y_{i}^{s}\right)\right\}_{i=1}^{m^{s}}$ , where  $x_{i}^{s}$  is the  $i$-th image sample in the source domain and  $y_{i}^{s} \in\{1, \ldots, C\}$  is its class label. In the target domain, we have a set of  $m^{t}$  labeled samples,  $\mathcal{D}^{t}=\left\{\left(x_{i}^{t}, y_{i}^{t}\right)\right\}_{i=1}^{m^{t}}$ , and a set of  $m^{u}$  unlabeled target samples,  $\mathcal{D}^{u}=\left\{x_{i}^{u}\right\}_{i=1}^{m^{m}}$ . Then we consider the problem of improving the classification performance using not only  $\mathcal{D}^{s}$  but also  $\left\{\mathcal{D}^{t}, \mathcal{D}^{u}\right\}$ , after adapting  $\left\{\mathcal{D}^{t}, \mathcal{D}^{u}\right\}$  to  $\mathcal{D}^{s}$ . Since we have the labeled samples  $\mathcal{D}^{t}$  in the target domain, this problem is called semi-supervised domain adaptation.

2.2 模型概念图

　　

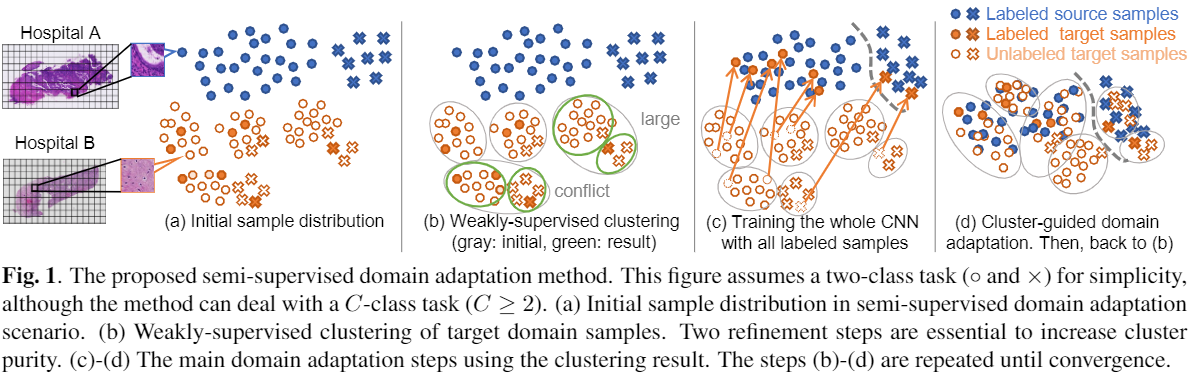
2.3 方法简介

2.3.1 弱监督聚类

通过软约束聚类优化聚类

　　第一个聚类优化步骤旨在将每个冲突的聚类（即具有来自不同类别标签的样本的聚类）划分为几个不冲突的聚类。

为此，我们使用“软”约束聚类 [10]。 通常，约束聚类引入了两种类型的约束，称为必须链接和不能链接。 必须链接给一对应该分组到同一个集群的样本，而不能链接给不应该分组的样本。

　　在我们的任务中，如果我们在同一个初始簇中找到具有不同标签的样本（通过 k-means），则不能将链接附加到这些样本的所有对。 类似地，如果我们在初始集群中找到具有相同标签的样本，则必须将链接附加到它们。 链接附加后，我们再次执行聚类，同时满足链接的约束。 再次注意，我们使用“软”约束聚类。 由于普通约束聚类，例如硬约束聚类，可能会由于远距离样本的必须链接而导致低纯度聚类，因此我们使用软约束聚类，这允许违反此类必须链接。 应用此步骤后，集群中标记的目标样本始终属于一个类。

　　

通过基于比例的分裂进行聚类细化

　　第二个聚类细化步骤旨在根据类比例 $\left(p_{1}, \ldots, p_{C}\right)$（即先验类概率）将聚类拆分为更小的聚类，这是由标记的目标样本之间的类比推断的。 这个目标类似于前面的细化步骤，但使用不同的标准。 粗略地说，在第一次细化之后，如果我们发现一个包含一个或多个标记样本的大集群，则该集群将是一个非纯集群，应该将其拆分为更小的集群。

　　更具体地说，我们通过使用类比例将较大的集群分成较小的集群。 $\bar{c}_{i}$ 表示第 $i$ 个簇中标记样本的类别，$u_{i}$ 是第 $i$ 个簇中未标记样本的数量。 那么，如果 $m^{u} p_{\bar{c}_{i}} \leq  u_{i}$ ，我们认为集群对于类 $\bar{c}_{i}$ 来说太大了，因此通过 k-means (k = 2) 将其分成两个较小的集群。 因此，即使是小类，我们也可以期待高纯度的簇。

2.3.2 集群引导域适应

　　使用上述谨慎步骤给出的聚类结果，我们现在执行聚类引导的域自适应，如 Figs.(c) 和 Figs.(d) 所示。 CNN 模型 $f$ 针对两个目标进行训练。 一种是通过交叉熵损失对所有标记样本 $\mathcal{D}^{s} \cup \mathcal{D}^{t}$ 进行分类，使源样本和标记目标样本靠得更近，如 $Fig. \square(\mathrm{c})$ 所示。 另一种是引导未标记样本 $x_{j}^{u}$ 重新训练后更接近属于同一簇的标记样本 $\boldsymbol{x}_{i}^{t}$（即 $\boldsymbol{x}_{i}^{t}$ 比属于 a 的 $x_{l}^{u}$ 更接近属于同一簇的 $\boldsymbol{x}_{j}^{u}$ 不同的集群）。 更具体地说，我们通过以下目标训练模型：

　　　　$\begin{array}{l}\mathcal{L}_{\mathrm{clu}}\left(\boldsymbol{x}_{i}^{t}, \boldsymbol{x}_{j}^{u}, \boldsymbol{x}_{l}^{u}\right)= \max \left\{\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}^{t}\right)-\boldsymbol{f}\left(\boldsymbol{x}_{j}^{u}\right)\right\|_{2}^{2}-\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}^{t}\right)-\boldsymbol{f}\left(\boldsymbol{x}_{l}^{u}\right)\right\|_{2}^{2}+\varepsilon, 0\right\}\end{array}$

　　其中 $f(x)$ 表示样本 $x$ 的特征向量，$\varepsilon \in \Re^{+}$ 是边距。 如 $Fig.1(d)$ 所示，通过使用这种损失训练 $f$ 以及标记样本 $x_{i}^{t}$ 的引导，将未标记样本逐渐映射到源域的相应类。 请注意，在此框架中，我们没有为未标记样本提供任何伪标签——未标记样本被用作未标记样本，以帮助使用 $Eq. (1)$ 中标记样本进行表示学习。

3 实验

可视化

　　

4 总结

　　略