zkw线段树——简单易懂好写好调的线段树

0.简介

zkw线段树是一种非递归线段树，与普通线段树不同的是，它是棵标准的满二叉树，所以遍历过程可全程使用位运算，常数一般比线段树小得多。

1.结构/建树

前面说了，zkw线段树是满二叉树，可是原数组大小不一定是2^n，所以我们就多开一些废点，硬充，另外，它需要左右各两个点当哨兵，原因看下面的查询原理就知道了。

有人会想，开一些废点是不是空间会更大，相反，一般线段树由于相比之下结构混乱，一般开4倍，而zkw只用开3倍。

这就是zkw：

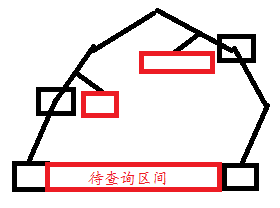
在zkw线段树中，最下面一排的点就是原数组上的点，因为是满二叉树，所以这些点的深度都一样，设为d（1的深度为0，图中d为4），然后会发现底排上面的点（从1~15）数量刚好为2^d-1，原数组中的元素编号（最底下红色字体）对应的线段树上的点的编号恰好增加了2^d，最低排点数也为2^d（包括废点），那么我们只需要知道这个常数d，就可以确定这棵树的结构了，所以建树很简单，只需要计算最小的、使最低排点数足够的d，实际上，计算2^d后面更方便：

int M; //M 即 2^d
void maketree(int n) {//原数组长度
    M = 1; while(M < n+2/*包括哨兵*/) M <<= 1;
}

2.单点修改

我们知道了2^d，就可以直接求出原数组中某个元素在线段树上的点，然后一路向上更新（编号/2下取整即为其父亲的编号）：

void addtree(int x,int y) {//y的类型视情况而变
    int s = M + x;
    tre[s] = y; s >>= 1;
    while(s) {
        tre[s] = Merge(tre[s<<1],tre[s<<1|1]);//自定义的某种合并操作，可以是相加、相乘、最大值最小值等
        s >>= 1;
    }
}

3.区间查询

当我们知道要查询的区间[l，r]时，就把区间两端往外的两个点记录为s(M+(l-1))，t(M+(r+1))，那么两点到 lca 路径包围住的点就恰好是要查询的区间，把s和t往父亲方向走，每当s为其父亲的左儿子（s为偶数），那它的兄弟一定在区间里（s ^ 1），每当t为其父亲的右儿子（t为奇数），那它的兄弟也一定在区间里（t ^ 1）：

int findtree(int l,int r) {
    int s = M + l - 1,t = M + r + 1;
    int ans = 0;
    while(s || t) {
        if((s>>1) ^ (t>>1)) { // s/2 != t/2
            if(!(s & 1)) ans = Merge(ans,tre[s ^ 1]);
            if(t & 1) ans = Merge(ans,tre[t ^ 1]);
        }
        else break;
        s >>= 1;t >>= 1;
    }
    return ans;
}

4.永久化懒标记

zkw线段树的修改和查询都是从下往上做，因此懒标记不方便往下放，于是就用永久化的懒标记，记录整个子树的修改（不包括子树的根），以后每次查询都要按照深度依次修改答案。

用懒标记就可以支持不按时间顺序修改的区间修改了，和不用懒标记的区间查询差不多，但是要修改访问到的区间内点的懒标记，并且更新经过的所有节点，也就是说不能中途break了。

以区间最大值为例：

void addtree(int l,int r,int y) { //区间修改
	int s = M + l - 1,r = M + r + 1;
	while(s || t) {
		if(s < M) tre[s] = max(tre[s<<1],tre[s<<1|1]) + lz[s]; //lz[]为懒标记数组
		if(t < M) tre[t] = max(tre[t<<1],tre[t<<1|1]) + lz[t]; //路途中的节点修改，但不包括最下面一排，因为它们没有子节点
		if((s>>1) ^ (t>>1)) {
			if(!(s & 1)) tre[s^1] += y,lz[s^1] += y;
			if(t & 1) tre[t^1] += y,lz[t^1] += y;
		} //不能break
		s >>= 1;t >>= 1;
	}
}
void findtree(int l,int r) { //区间查询
	int s = M + l - 1,r = M + r + 1;
	int ls = 0,rs = 0; //左右两边单独算，因为左边每一个父亲只能照顾左边路径上的子孙，右边同理
	while(s || t) {
		ls += lz[s];
		rs += lz[t];
		if((s>>1) ^ (t>>1)) {
			if(!(s & 1)) ls = max(ls,tre[s^1]); //这里不能考虑懒标记，因为懒标记省略的修改不包括自己
			if(t & 1) rs = max(rs,tre[t^1]);    //当然，这只是笔者个人的写法，看官随意
		}
		s >>= 1;t >>= 1;
	}
	return max(ls,rs);
}

5.其他

除了这些操作，zkw还可以支持线段树二分，只不过只有到最底层的时候，才能知道具体的位置。

记录每个点的具体区间范围、长度，甚至可以将就打递归版。

此外，zkw线段树结构的性质还可以运用到其他题目上。