2021-2022 ICPC, NERC, Northern Eurasia Onsite (Unrated, Online Mirror, ICPC Rules, Teams Preferred) J. Job Lookup

题意

n个节点，n<=200，你需要构造这n个几点成为一棵树，并且这棵树的中序遍历为1-n;

你构造树的节点之间的最短路构成一个n×n的最短距离矩阵d；

同时给你n×n的权重矩阵c；最最小的Σdij*cij

思路

1. 显然，中序遍历，对于根节点来说，左边的序号小于根，右边的需要大于根

2. cij同化成对于i，j之间的最短路上，每条边增加cij，这样相当于对每条边考虑了

3. 下面就是常规套路了，区间dp，dp[l][r]代表范围l-r构成的子树，求和的最小值



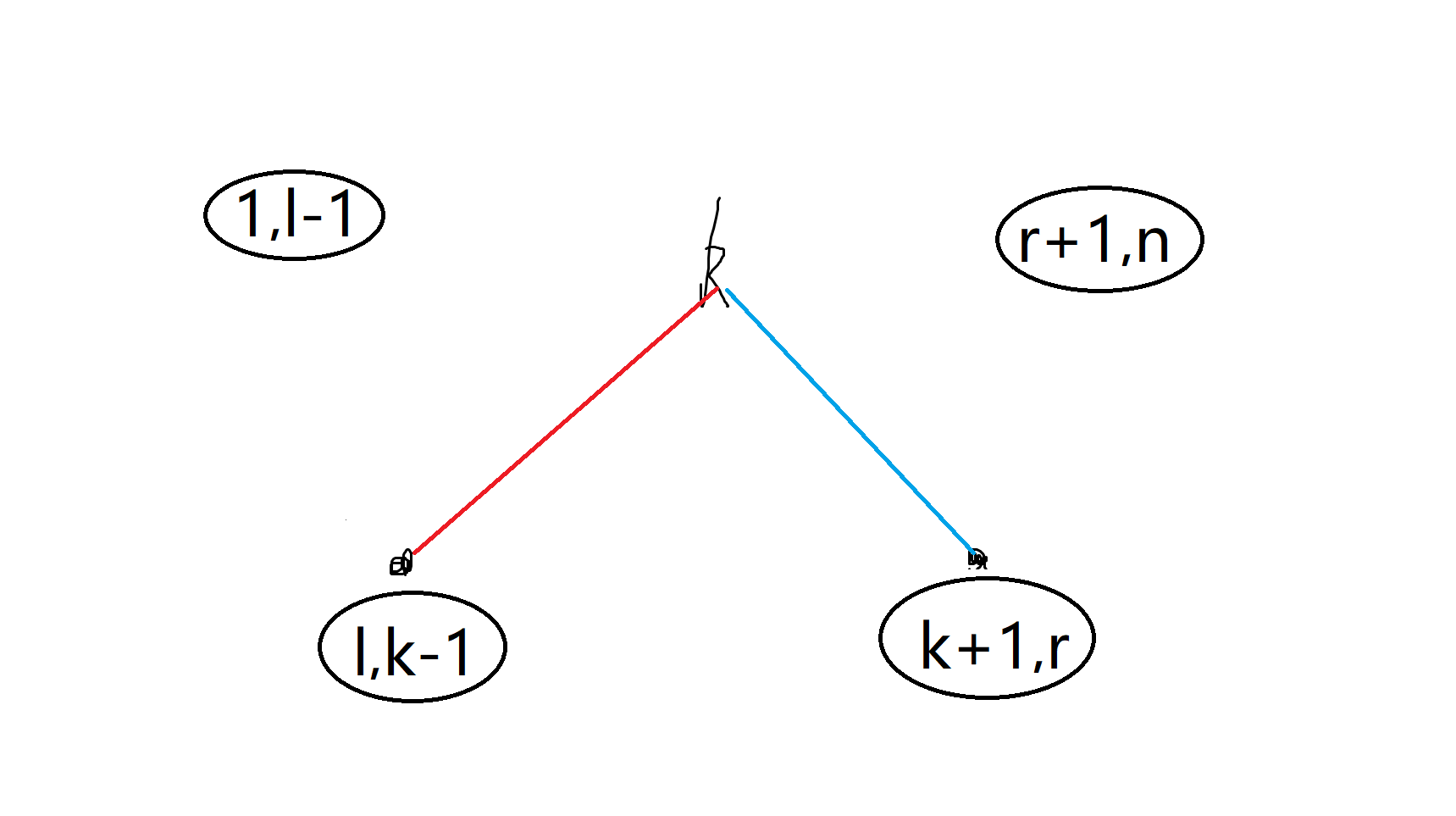
枚举l，r的根节点k，显然需要dp[l][r]+=dp[l][k-1]+dp[k+1][r]

其次，需要分别统计红色，蓝色线的价值，即左子树内的几点到其他节点，以及右子树内的点到其他节点的价值，这相当与cij的子矩阵求和；

这个可以对cij进行前缀和预处理计算得出

代码

#include<bits/stdc++.h>

using namespace std;
long long a[205][205];
long long dp[205][205];
int ans[205];
int f[205][205];

int res(int l, int r) {
    if (r < l)return 0;
    int k = f[l][r];
    ans[res(l, k - 1)] = k;
    ans[res(k + 1, r)] = k;
    return k;
}

long long clc(int l, int r, int ll, int rr) {
    if (l > r || ll > rr)return 0;
    return a[r][rr] - a[l - 1][rr] - a[r][ll - 1] + a[l - 1][ll - 1];
}

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> a[i][j];
            a[i][j] = (a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + a[i][j]);
        }
    }
//    memset(dp, 0x3f, sizeof dp);
//    for (int i = 1; i <= n; i++)for (int j = i; j <= n; j++)dp[i][j] = 1e18;
//    for (int len = 1; len <= n; len++) {
//        for (int l = 1; l + len - 1 <= n; l++) {
//            int r = l + len - 1;
//            for (int k = l; k <= r; k++) {
//                long long v = dp[l][k - 1] + dp[k + 1][r] ;
//                v += clc(1, l - 1, l, k - 1) + clc(l, k - 1, k, n);
//                v += clc(1, k, k + 1, r) + clc(k + 1, r, r + 1, n);
//                if (v < dp[l][r]) {
//                    dp[l][r] = v;
//                    f[l][r] = k;
//                }
//            }
//        }
//    }
    memset(dp, 0x3f, sizeof dp);
    for (int i = 0; i <= n; i++)dp[i][i] = 0, f[i][i] = i;
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            for (int k = l; k <= r; k++) {

                //long long v = ((l <= k - 1) ? dp[l][k - 1] : 0 )+ ((k + 1 <= r) ? dp[k + 1][r] : 0);
                long long v = ((l < k - 1) ? dp[l][k - 1] : 0 )+ ((k + 1 < r) ? dp[k + 1][r] : 0);
//                if (v != vv) {
//                    cout << l<< ' ' <<k<<' '<< r<<'\n';
//                    cout << dp[l][k - 1] << ' ' << dp[k + 1][r]<<'\n';
//                }
                v += clc(1, l - 1, l, k - 1) + clc(l, k - 1, k, n);
                v += clc(1, k, k + 1, r) + clc(k + 1, r, r + 1, n);
                if (v <= dp[l][r]) {
                    dp[l][r] = v;
                    f[l][r] = k;
                }
            }
        }
    }
//    cout << dp[1][n] << '\n';
    res(1, n);
    for (int i = 1; i <= n; i++) {
        cout << ans[i] << ' ';
    }

    return 0;
}