JZOJ 4319. 【NOIP2015模拟11.5】Lucas的数列

题目

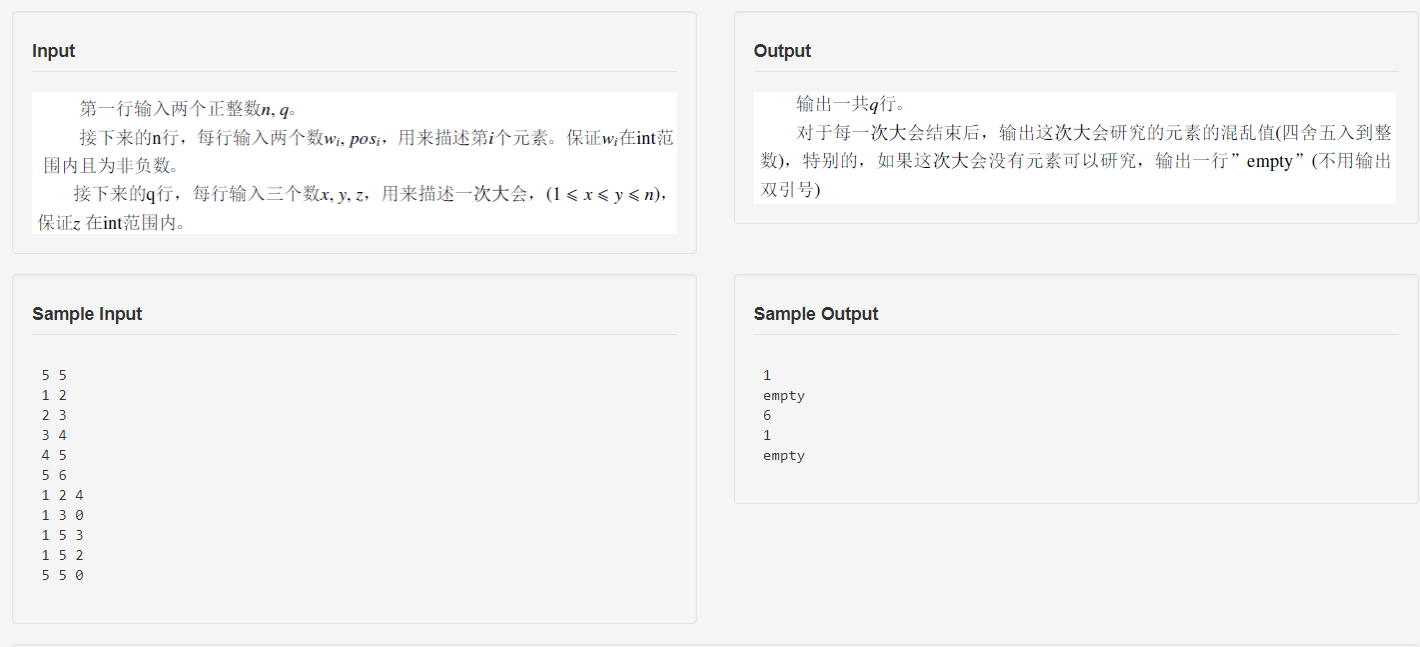
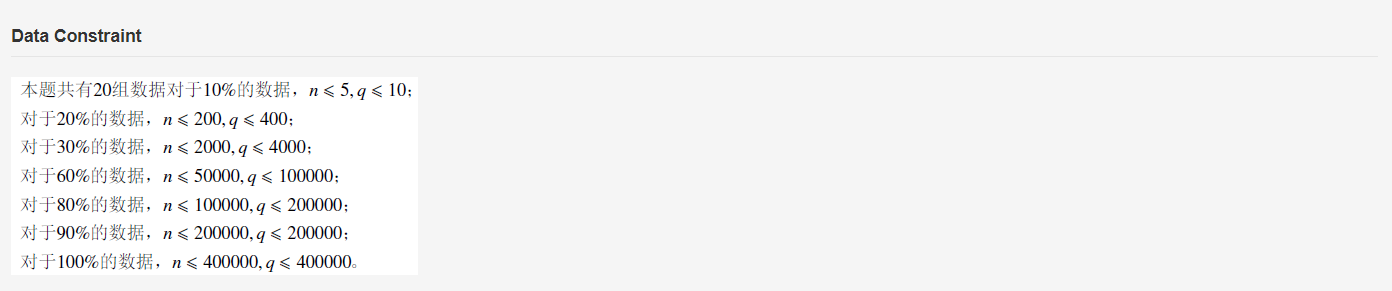
思路

暴力很好打，我们显然可以先把关于 \(k\) 的式子拆开

先二项式展开，然后把外面的 \(m\) 乘进去，把 \(p\) 的分母 \(m\) 消去

\(K = (\sum_{i=1}^m (x_i - p)^2) \times m = m \times \sum_{i=1}^m x_i^2 - (\sum_{i=1}^m x_i)^2\)

发现它只剩下整数的乘和减运算

其实可以看出我们需要维护的东西：区间小于等于 \(z\) 的数的个数，这些数的和，这些数的平方的和

那么我们怎么维护区间小于等于 \(z\) 的数的信息呢？

对于这种二维偏序问题，经典的做法是在线的主席树

然而空间卡得不行不行的

所以我们考虑离线做法

依照题目意思，唯有 \(w \leq z\) 的数会对当前答案产生贡献

我们离线，先按照 \(w,z\) 从小到大排序

那么我们按这个顺序做下去，每遇到一个点就将其以它在原序列中的编号插入到某种数据结构中

遇到一个询问时，我们已经保证了 \(w \leq z\) 的数在这个数据结构中，只要查询区间 \([l..r]\) 的信息就好

因为空间的恶心，推荐使用树状数组

\(Code\)

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;

const int N = 4e5 + 5;
const LL INF = -1e18 - 1e15;
LL m , ps1 , ps2 , ans[N];
int n , q , h[N] , tot;

struct question{
	int to , nxt;
}c[N];

struct ask{
	int x , y , z , id;
}a[N];

struct node{
	int w , id;
	LL pos;
}b[N];

struct segment{
	int cnt;
	LL pos1 , pos2;
}seg[N];

inline bool cmp1(node x , node y){return x.w < y.w;}
inline bool cmp2(ask x , ask y){return x.z < y.z;}
inline void addask(int id1 , int id2){c[++tot].to = id2 , c[tot].nxt = h[id1] , h[id1] = tot;}
inline int lowbit(int x){return x & (-x);}

inline void update(int x , int ct , LL p1 , LL p2)
{
	for(; x <= n; x += lowbit(x))
		seg[x].cnt += ct , seg[x].pos1 += p1 , seg[x].pos2 += p2;
}

inline void query(int x , int fl)
{
	for(; x; x -= lowbit(x))
		m += (LL)seg[x].cnt * fl , ps1 += seg[x].pos1 * fl , ps2 += seg[x].pos2 * fl;
}

int main()
{
	freopen("sequence.in" , "r" , stdin);
	freopen("sequence.out" , "w" , stdout);
	scanf("%d%d" , &n , &q);
	for(register int i = 1; i <= n; i++) scanf("%d%lld" , &b[i].w , &b[i].pos) , b[i].id = i;
	for(register int i = 1; i <= q; i++) scanf("%d%d%d" , &a[i].x , &a[i].y , &a[i].z) , a[i].id = i;
	sort(b + 1 , b + n + 1 , cmp1) , sort(a + 1 , a + q + 1 , cmp2);

	int l , r , mid , res;
	for(register int i = 1; i <= q; i++)
	{
		l = 1 , r = n , mid , res = 0;
		while (l <= r)
		{
			mid = (l + r) >> 1;
			if (b[mid].w <= a[i].z) res = mid , l = mid + 1;
			else r = mid - 1;
		}
		if (res == 0) ans[a[i].id] = INF;
		else addask(res , i);
	}
	for(register int i = 1; i <= n; i++)
	{
		update(b[i].id , 1 , b[i].pos , b[i].pos * b[i].pos);
		for(register int j = h[i]; j; j = c[j].nxt)
		{
			int id = c[j].to;
			ps1 = ps2 = 0 , m = 0;
			query(a[id].y , 1) , query(a[id].x - 1 , -1);
			if (m == 0)
			{
				ans[a[id].id] = INF;
				continue;
			}
			ans[a[id].id] = m * ps2 - ps1 * ps1;
		}
	}
	for(register int i = 1; i <= q; i++)
	{
		if (ans[i] == INF) printf("empty\n");
		else printf("%lld\n" , ans[i]);
	}
}

其实这题有个很暴力的方法

分块大法好！！！

我们维护一个分块数组

它包括每个点的 \(w,pos\)

然后同一块内的数按 \(w\) 从小到大排序

维护前缀和包括一次方和二次方的

查询只需要二分找块中的位置

前缀和更新即可

\(Code\)

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long LL;

const int N = 4e5 + 5;
LL m , pos[N] , ps1 , ps2;
int n , q , w[N] , st[N] , ed[N] , num , belong[N];

struct node{
	int w;
	LL pos , pos1 , pos2;
}t[N];

inline bool cmp(node x , node y){return x.w < y.w;}

inline void parepre()
{
	num = (int)sqrt(n);
	for(register int i = 1; i <= num; i++) st[i] = n / num * (i - 1) + 1 , ed[i] = n / num * i;
	ed[num] = n;
	for(register int i = 1; i <= num; i++)
	{
		for(register int j = st[i]; j <= ed[i]; j++) belong[j] = i , t[j] = (node){w[j] , pos[j] , 0 , 0};
		sort(t + st[i] , t + ed[i] + 1 , cmp);
		for(register int j = st[i]; j <= ed[i]; j++)
		{
			(j == st[i] ? (t[j].pos1 = t[j].pos) : (t[j].pos1 = t[j - 1].pos1 + t[j].pos));
			(j == st[i] ? (t[j].pos2 = t[j].pos * t[j].pos) : (t[j].pos2 = t[j - 1].pos2 + t[j].pos * t[j].pos));
		}
	}
}

inline void query(int l , int r , int z)
{
	int x = belong[l] , y = belong[r];
	if (x == y)
	{
		for(register int i = l; i <= r; i++)
		if (w[i] <= z) m++ , ps1 += pos[i] , ps2 += pos[i] * pos[i];
		return;
	}
	for(register int i = l; i <= ed[x]; i++)
	if (w[i] <= z) m++ , ps1 += pos[i] , ps2 += pos[i] * pos[i];
	for(register int i = st[y]; i <= r; i++)
	if (w[i] <= z) m++ , ps1 += pos[i] , ps2 += pos[i] * pos[i];
	int l1 , r1 , mid , ret;
	for(register int i = x + 1; i <= y - 1; i++)
	{
		l1 = st[i] , r1 = ed[i] , ret = 0;
		while (l1 <= r1)
		{
			mid = (l1 + r1) >> 1;
			if (t[mid].w <= z) ret = mid , l1 = mid + 1;
			else r1 = mid - 1;
		}
		if (ret) m += ret - st[i] + 1 , ps1 += t[ret].pos1 , ps2 += t[ret].pos2;
	}
}

int main()
{
	freopen("sequence.in" , "r" , stdin);
	freopen("sequence.out" , "w" , stdout);
	scanf("%d%d" , &n , &q);
	for(register int i = 1; i <= n; i++) scanf("%d%lld" , &w[i] , &pos[i]);
	parepre();
    int x , y , z;
	while (q--)
	{
		scanf("%d%d%d" , &x , &y , &z);
		ps1 = ps2 = 0 , m = 0;
		query(x , y , z);
		if (m == 0)
		{
			printf("empty\n");
			continue;
		}
		LL k = m * ps2 - ps1 * ps1;
		printf("%lld\n" , k);
	}
}