论文解读（SUBG-CON）《Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning》

论文信息

论文标题：Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning
论文作者：Yizhu Jiao, Yun Xiong, Jiawei Zhang, Yao Zhang, Tianqi Zhang, Yangyong Zhu
论文来源：2020 ICDM
论文地址：download 
论文代码：download

1 Introduction

　　创新点：提出一种新的子图对比度自监督表示学习方法，利用中心节点与其采样子图之间的强相关性来捕获区域结构信息。

　　与之前典型方法对比：

　　

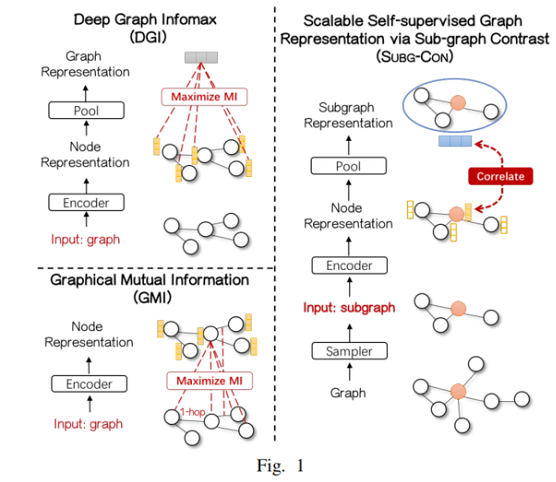
2 Method

2.1 Subgraph-Based Self-Supervised Representation Learning

　　对于中心节点 $i$，设计了一个子图采样器 $\mathcal{S}$，从原始图中提取其上下文子图 $\mathbf{X}_{i} \in \mathbb{R}^{N^{\prime} \times F}$。上下文子图为学习节点 $i $ 的表示提供了区域结构信息。其中，$\mathbf{X}_{i} \in \mathbb{R}^{N^{\prime} \times F}$ 表示第  $i$  个上下文子图的节点特征矩阵。$\mathbf{A}_{i}$ 表示节点 $i$ 邻居的邻接矩阵。$N^{\prime}$ 表示上下文子图的大小。

　　目标是学习一个上下文子图的编码器  $\mathcal{E}: \mathbb{R}^{N^{\prime} \times F} \times \mathbb{R}^{N^{\prime} \times N^{\prime}} \rightarrow \mathbb{R}^{N^{\prime} \times F^{\prime}}$ ，用于获取上下文图中的节点表示。

　　注意：

• • 子图采样器 $S$ ：作为一种数据增强的手段，需要计算邻居重要性得分，并对重要节点进行采样，从而组成一个上下文子图，为中心节点提供领域结构信息。　　
  • 子图编码器 $\mathcal{E} $：需要计算中心节点 $i$ 的表示，还要根据子图信息生成子图表示 $s_i$　　

2.2  Subgraph Sampling Based Data Augmentation

　　重要性得分矩阵 $\mathcal{S}$ 可以记为：【邻居节点连的节点越多越不重要】

　　　　$\mathbf{S}=\alpha \cdot(\mathbf{I}-(1-\alpha) \cdot \overline{\mathbf{A}})\quad\quad\quad\quad(1)$

　　其中

• • $\overline{\mathbf{A}}=AD^{-1}$；
  • $S(i，：)$ 为节点 $i$ 的重要度得分向量，表示它与其他节点的相关性；
  • $\alpha \in[0,1] $ 是一个参数，它总是被设置为 $0.15 $；

　　对于一个特定的节点 $i$ ，子图采样器 $S$ 选择 $top-k$ 重要的邻居，用得分矩阵 $S$ 组成一个子图。所选节点的指数可以记为

　　　　$i d x=\text { top_rank }(\mathbf{S}(i,:), k)$

　　其中，$\text { top_rank }$ 是返回顶部 $k$ 值的索引的函数，$k$ 表示上下文图的大小。

　　然后，可以使用上述产生的 $ids$ 生成子图邻接矩阵 $A_i$、特征矩阵$X$：

　　　　$\mathbf{X}_{i}=\mathbf{X}_{i d x,:}, \quad \mathbf{A}_{i}=\mathbf{A}_{i d x, i d x}$

　　到目前为止可以生成上下文子图 $ \mathcal{G}_{i}=   \left(\mathbf{X}_{i}, \mathbf{A}_{i}\right) \sim \mathcal{S}(\mathbf{X}, \mathbf{A})$ 。

2.3  Encoding Subgraph For Representations

　　给定中心节点 $i$ 的上下文子图 $\mathcal{G}_{i}=\left(\mathbf{X}_{i}, \mathbf{A}_{i}\right) $，编码器 $\mathcal{E}: \mathbb{R}^{N^{\prime} \times F} \times \mathbb{R}^{N^{\prime} \times N^{\prime}} \rightarrow \mathbb{R}^{N^{\prime} \times F^{\prime}}$ 对其进行编码，得到潜在表示矩阵 $\mathbf{H}_{i} $ 表示为

　　　　$\mathbf{H}_{i}=\mathcal{E}\left(\mathbf{X}_{i}, \mathbf{A}_{i}\right)$

　　　　$\mathbf{h}_{i}=\mathcal{C}\left(\mathbf{H}_{i}\right)$

　　其中，$\mathcal{C}$ 表示选择中心节点表示的操作。

　　我们利用一个读出函数 $\mathcal{R} : \mathbb{R}^{N^{\prime} \times F^{\prime}} \rightarrow \mathbb{R}^{F^{\prime}}$，并使用它将获得的节点表示总结为子图级表示 $\mathbf{s}_{i}$，记为

　　　　$\mathbf{s}_{i}=\mathcal{R}\left(\mathbf{H}_{i}\right)$

　　其实就是 $\mathcal{R}(\mathbf{H})=\sigma\left(\frac{1}{N^{\prime}} \sum\limits _{i=1}^{N^{\prime}} \mathbf{h}_{i}\right)$

2.4 Contrastive Learning via Central Node and Context Subgraph

　　整体框架如下所示：

　　 

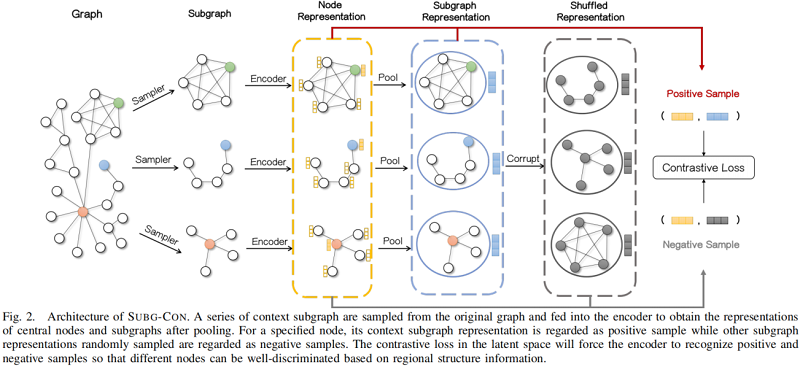
　　对于捕获上下文子图中的区域信息的节点表示 $h_i$，我们将上下文子图表示 $s_i$ 视为正样本。另一方面，对于一组子图表示，我们使用一个 Corruption functions $\mathcal{P}$ （其实就是 shuffle 操作）来破坏它们以生成负样本，记为

　　　　$\left\{\widetilde{\mathbf{s}}_{1}, \widetilde{\mathbf{s}}_{2} \ldots, \widetilde{\mathbf{s}}_{M}\right\} \sim \mathcal{P}\left(\left\{\mathbf{s}_{1}, \mathbf{s}_{2}, \ldots, \mathbf{s}_{m}\right\}\right)$

　　其中，$m$ 是表示集的大小。

　　采用三联体损失函数（triplet loss）：

　　　　$\mathcal{L}=\frac{1}{M} \sum\limits _{i=1}^{M} \mathbb{E}_{(\mathbf{X}, \mathbf{A})}\left(-\max \left(\sigma\left(\mathbf{h}_{i} \mathbf{s}_{i}\right)-\sigma\left(\mathbf{h}_{i} \widetilde{\mathbf{s}}_{i}\right)+\epsilon, 0\right)\right)\quad\quad\quad(2)$

　　算法流程如下：

　　 

3 Experiment

数据集

　　

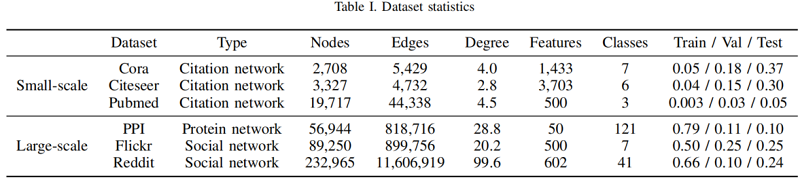
实验细节

不同编码器对比

　　对于 Cora、Citeseer、Pubmed、PPI 采用带跳跃连接的一层的 GCN 编码器：

　　　　$\mathcal{E}(\mathbf{X}, \mathbf{A})=\sigma\left(\hat{\mathbf{D}}^{-\frac{1}{2}} \hat{\mathbf{A}} \hat{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \mathbf{W}+\hat{\mathbf{A}} \mathbf{W}_{s k i p}\right)$

　　其中：$\mathbf{W}_{s k i p}\$ 是跳跃连接的可学习投影矩

　　对于 Reddit、Flickr 采用两层的 GCN 编码器：

　　　　$\begin{array}{c}G C N(\mathbf{X}, \mathbf{A})=\sigma\left(\hat{\mathbf{D}}^{-\frac{1}{2}} \hat{\mathbf{A}} \hat{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \mathbf{W}\right) \\\mathcal{E}(\mathbf{X}, \mathbf{A})=G C N(G C N(\mathbf{X}, \mathbf{A}), \mathbf{A})\end{array}$

　　对比结果：

　　 

不同的目标函数：

　　 

　　对比结果：

　　

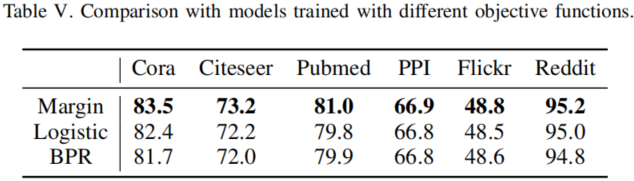
子图距离对比

　　

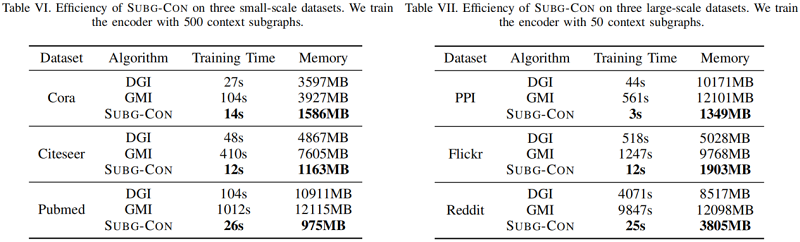
训练时间和内存成本

　　

子图大小分析

　　

4 Conclusion

　　在本文中，我们提出了一种新的可扩展的自监督图表示，通过子图对比，子V.。它利用中心节点与其区域子图之间的强相关性进行模型优化。基于采样子图实例，子g-con在监督要求较弱、模型学习可扩展性和并行化方面具有显著的性能优势。通过对多个基准数据集的实证评估，我们证明了与有监督和无监督的强基线相比，SUBG-CON的有效性和效率。特别地，它表明，编码器可以训练良好的当前流行的图形数据集与少量的区域信息。这表明现有的方法可能仍然缺乏捕获高阶信息的能力，或者我们现有的图数据集只需要驱虫信息才能获得良好的性能。我们希望我们的工作能够激发更多对图结构的研究，以探索上述问题。