论文解读(MERIT)《Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning》
论文信息
论文标题:Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning
论文作者:Ming Jin, Yizhen Zheng, Yuan-Fang Li, Chen Gong, Chuan Zhou, Shirui Pan
论文来源:2021, IJCAI
论文地址:download
论文代码:download
1 Introduction
创新:融合交叉视图对比和交叉网络对比。
2 Method
算法图示如下:
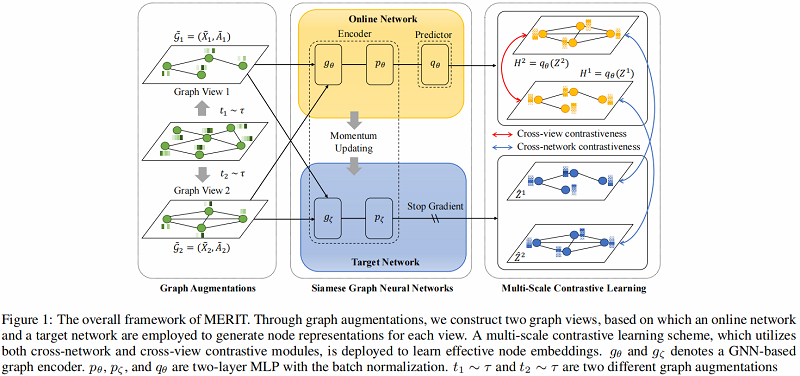
模型组成部分:
- Graph augmentations
- Cross-network contrastive learning
- Cross-view contrastive learning
2.1 Graph Augmentations
- Graph Diffusion (GD)
$S=\sum\limits _{k=0}^{\infty} \theta_{k} T^{k} \in \mathbb{R}^{N \times N}\quad\quad\quad(1)$
这里采用 PPR kernel:
$S=\alpha\left(I-(1-\alpha) D^{-1 / 2} A D^{-1 / 2}\right)^{-1}\quad\quad\quad(2)$
- Edge Modification (EM)
给定修改比例 $P$ ,先随机删除 $P/2$ 的边,再随机添加$P/2$ 的边。(添加和删除服从均匀分布)
- Subsampling (SS)
在邻接矩阵中随机选择一个节点索引作为分割点,然后使用它对原始图进行裁剪,创建一个固定大小的子图作为增广图视图。
- Node Feature Masking (NFM)
给定特征矩阵 $X$ 和增强比 $P$,我们在 $X$ 中随机选择节点特征维数的 $P$ 部分,然后用 $0$ 掩码它们。
在本文中,将 SS、EM 和 NFM 应用于第一个视图,并将 SS+GD+NFM 应用于第二个视图。
2.2 Cross-Network Contrastive Learning
MERIT 引入了一个孪生网络架构,它由两个相同的编码器(即 $g_{\theta}$, $p_{\theta}$, $g_{\zeta}$ 和 $p_{\zeta}$)组成,在 online encoder 上有一个额外的预测器$q_{\theta}$,如 Figure 1 所示。
这种对比性的学习过程如 Figure 2(a) 所示:

其中:
- $H^{1}=q_{\theta}\left(Z^{1}\right)$
- $Z^{1}=p_{\theta}\left(g_{\theta}\left(\tilde{X}_{1}, \tilde{A}_{1}\right)\right)$
- $Z^{2}=p_{\theta}\left(g_{\theta}\left(\tilde{X}_{2}, \tilde{A}_{2}\right)\right)$
- $\hat{Z}^{1}=p_{\zeta}\left(g_{\zeta}\left(\tilde{X}_{1}, \tilde{A}_{1}\right)\right)$
- $\hat{Z}^{2}=p_{\zeta}\left(g_{\zeta}\left(\tilde{X}_{2}, \tilde{A}_{2}\right)\right)$
参数更新策略(动量更新机制):
$\zeta^{t}=m \cdot \zeta^{t-1}+(1-m) \cdot \theta^{t}\quad\quad\quad(3)$
其中,$m$、$\zeta$、$\theta$ 分别为动量参数、target network 参数和 online network 参数。
损失函数如下:
$\mathcal{L}_{c n}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left(\mathcal{L}_{c n}^{1}\left(v_{i}\right)+\mathcal{L}_{c n}^{2}\left(v_{i}\right)\right)\quad\quad\quad(6)$
其中:
$\mathcal{L}_{c n}^{1}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, \hat{z}_{v_{i}}^{2}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, \hat{z}_{v_{j}}^{2}\right)\right)}}\quad\quad\quad(4) $
$\mathcal{L}_{c n}^{2}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{2}, \hat{z}_{v_{i}}^{1}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{2}, \hat{z}_{v_{j}}^{1}\right)\right)}}\quad\quad\quad(5) $
2.3 Cross-View Contrastive Learning
损失函数:
$\mathcal{L}_{c v}^{k}\left(v_{i}\right)=\mathcal{L}_{\text {intra }}^{k}\left(v_{i}\right)+\mathcal{L}_{\text {inter }}^{k}\left(v_{i}\right), \quad k \in\{1,2\}\quad\quad\quad(10)$
其中:
$\mathcal{L}_{c v}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left(\mathcal{L}_{c v}^{1}\left(v_{i}\right)+\mathcal{L}_{c v}^{2}\left(v_{i}\right)\right)\quad\quad\quad(9)$
$\mathcal{L}_{\text {inter }}^{1}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{j}}^{2}\right)\right)}}\quad\quad\quad(7) $
$\begin{aligned}\mathcal{L}_{i n t r a}^{1}\left(v_{i}\right) &=-\log \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)}{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)+\Phi} \\\Phi &=\sum\limits_{j=1}^{N} \mathbb{1}_{i \neq j} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{j}}^{1}\right)\right)\end{aligned}\quad\quad\quad(8)$
2.4 Model Training
$\mathcal{L}=\beta \mathcal{L}_{c v}+(1-\beta) \mathcal{L}_{c n}\quad\quad\quad(11)$
3 Experiment
数据集
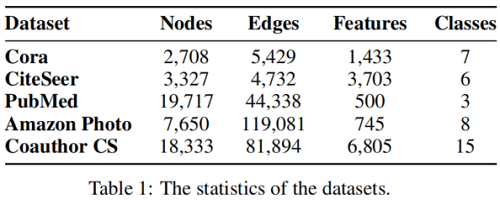
基线实验
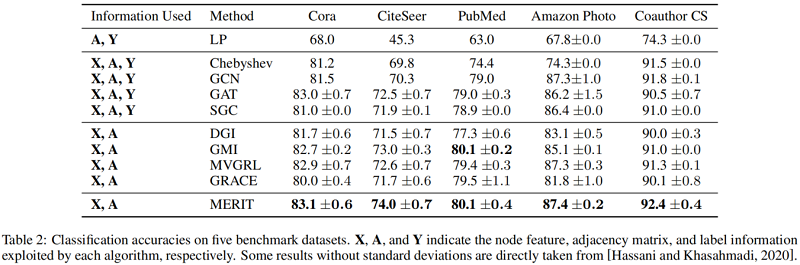
论文解读(MERIT)《Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning》的更多相关文章
- 论文解读(SUBG-CON)《Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning》
论文信息 论文标题:Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning论文作者:Yizhu Ji ...
- 论文解读(GMI)《Graph Representation Learning via Graphical Mutual Information Maximization》2
Paper Information 论文作者:Zhen Peng.Wenbing Huang.Minnan Luo.Q. Zheng.Yu Rong.Tingyang Xu.Junzhou Huang ...
- 论文解读(GMI)《Graph Representation Learning via Graphical Mutual Information Maximization》
Paper Information 论文作者:Zhen Peng.Wenbing Huang.Minnan Luo.Q. Zheng.Yu Rong.Tingyang Xu.Junzhou Huang ...
- 论文解读(GRCCA)《 Graph Representation Learning via Contrasting Cluster Assignments》
论文信息 论文标题:Graph Representation Learning via Contrasting Cluster Assignments论文作者:Chun-Yang Zhang, Hon ...
- 论文解读GALA《Symmetric Graph Convolutional Autoencoder for Unsupervised Graph Representation Learning》
论文信息 Title:<Symmetric Graph Convolutional Autoencoder for Unsupervised Graph Representation Learn ...
- 论文解读(SUGRL)《Simple Unsupervised Graph Representation Learning》
Paper Information Title:Simple Unsupervised Graph Representation LearningAuthors: Yujie Mo.Liang Pen ...
- 论文阅读 Dynamic Graph Representation Learning Via Self-Attention Networks
4 Dynamic Graph Representation Learning Via Self-Attention Networks link:https://arxiv.org/abs/1812. ...
- 论文解读(MVGRL)Contrastive Multi-View Representation Learning on Graphs
Paper Information 论文标题:Contrastive Multi-View Representation Learning on Graphs论文作者:Kaveh Hassani .A ...
- 论文笔记:Deeper and Wider Siamese Networks for Real-Time Visual Tracking
Deeper and Wider Siamese Networks for Real-Time Visual TrackingUpdated on 2019-04-01 16:10:37 Paper ...
随机推荐
- 半吊子菜鸟学Web开发1 --配置开发环境
先说说我自己的情况,我算是一个半吊子菜鸟,对web开发熟练度为0,但是对熟悉C++和Python 所以这里开始记录我学习Web开发的历程,看看我这里学习的程序,能够学到什么地方. 首先是配置环境,我的 ...
- 阿里云删除mysql
记录以下,学生买的轻量级服务器安装mysql之后发现没有初始密码,之后在被自己七搞八搞后彻底歇菜,就准备重新卸载安装 记录自己卸载过程首先运行rpm -qa | grep -i mysql出来的是:m ...
- Flask-SQLAlchemy 使用教程
Flask-SQLAlchemy ,是对SQLAlchemy进一步封装 SQLAlchemy使用教程地址: https://www.cnblogs.com/bigox/p/11552542.html ...
- 学习zabbix(一)
一.zabbix监控简介 server: 通过收集snmp和agent发送的数据,写入数据库(MySQL,ORACLE),再通过 php+apache 在 web 前端展示. agent:主机通过安装 ...
- Netty学习摘记 —— Netty客户端 / 服务端概览
本文参考 本篇文章是对<Netty In Action>一书第二章"你的第一款 Netty 应用程序"的学习摘记,主要内容为编写 Echo 服务器和客户端 第一款应用程 ...
- Excel之“提取指定符号(中括号)中的字符”
提取A1中[]内的字符函数:=MID(A1,SEARCH("[",A1)+1,SEARCH("]",A1)-SEARCH("[",A1)-1 ...
- Easyx库安装教程
目录: 安装 使用 帮助文档 安装 打开Easyx官网https://easyx.cn/ 点击图中下载按钮,下载Easyx库.或者直接点此下载 双击运行 图中标注的绿色框内为官方提供的帮助文档,红色框 ...
- 深入理解ES6之《ES7》
指数运算符 Math.pow是可以进行求幂运算的求幂运算符是两个星号 let result = 5 ** 2 console.log(result) //25 console.log(result = ...
- 从路由原理出发,深入阅读理解react-router 4.0的源码
react-router等前端路由的原理大致相同,可以实现无刷新的条件下切换显示不同的页面.路由的本质就是页面的URL发生改变时,页面的显示结果可以根据URL的变化而变化,但是页面不会刷新.通过前 ...
- 一个命令完成[打包+同步七牛cdn+上传服务器]
webpack+gulp+qshell+npm-scripts实现一个命令完成[打包+同步cdn+上传服务器] 说明 由于我们用的七牛云存储,所以cdn也是走的七牛,所以并不适用于其他的cdn,但是思 ...
