python不确定性计算之粗糙集属性约简
粗糙集属性约简
本实验同时采用区别矩阵和依赖度约简。
在依赖度约简中,设置依赖度计算函数和相对约简函数,对读取的数据进行处理,最后根据依赖度约简。
在读取数据后判断有无矛盾,若有则进行决策表分解,然后进行区别矩阵约简得到约简后的条件属性。
区分矩阵代码如下:
import xlrd #读取Excel的扩展工具
from copy import deepcopy
import numpy as np#numerical python
from pprint import pprint
import itertools
def read_excel(path):
#打开excel
x_matrix = []
workbook = xlrd.open_workbook(path,'r')
table = workbook.sheets()[0]
for rown in range(1,table.nrows):
x_matrix.append(table.row_values(rown))
x_matrix = np.array(x_matrix)
#print(x_matrix)
return x_matrix
#决策表分解
def divide(matrix):
len_attribute = len(matrix[0])-1
matrix_delete = []
#print(len(matrix))
#决策表分解
for j in range(len(matrix)):
for k in range(j,len(matrix)):
if ((matrix[j][0:len_attribute] == matrix[k][0:len_attribute]).all() and matrix[j][len_attribute] != matrix[k][len_attribute]):
matrix_delete.append(list(matrix[j]))
matrix_delete.append(list(matrix[k]))
matrix = np.delete(matrix,k,axis=0)
matrix = np.delete(matrix,j,axis=0)
if(len(matrix_delete)):
print('矛盾:',matrix_delete)
else:
print('不存在矛盾数据!')
print('-------------------------------------------')
if(len(matrix)):
print('完全一致表:')
pprint(matrix)
deal(matrix)
else:
print('不存在完全一致表:')
if(len(matrix_delete)):
print('完全不一致表:')
print(matrix_delete)
#约简
def deal(matrix):
matrix_T = matrix.T
number_sample = len(matrix)#样本数量
number_attribute = len(matrix_T)-1#属性数量
attribute = ['年龄','收入','学生','信誉']
# 二维列表的创建:
excel = [[ [] for col in range(number_sample)] for row in range(number_sample)]
pprint(matrix)
#比较各样本哪些属性的值不同(只对决策属性不同的个体进行比较)
for k in range(len(attribute)):#属性
for i in range(number_sample):#第几个样本
for j in range(i,number_sample):
if(matrix[i][k] != matrix[j][k] and matrix[i][number_attribute] != matrix[j][number_attribute]):
excel[i][j].append(attribute[k])
for i in range(number_sample):
for j in range(i,number_sample):
excel[j][i] = set(excel[i][j])
excel[i][j] = {}
#pprint(excel)#excel
yuejian = []
for i in range(number_sample):
for j in range(number_sample):
if(excel[i][j] and excel[i][j] not in yuejian):
yuejian.append(excel[i][j])
print(yuejian)
#约简
i=0
j=0
k=len(yuejian)#k=6
for i in range(k):
for j in range(k):
if(yuejian[i] > yuejian[j]):#i更大,应该删除i
yuejian[i] = yuejian[j]
if(yuejian[i] & yuejian[j]):
yuejian[i] = yuejian[i] & yuejian[j]
yuejian[j] = yuejian[i] & yuejian[j]
'''
#print(yuejian)
#去重
yuejian_new = []
for id in yuejian:
if id not in yuejian_new:
yuejian_new.append(id)
yuejian = yuejian_new
'''
#print('约简为:',yuejian)
#print('yuejian:',yuejian)
#类似于笛卡儿积
flag = 0
result =[]
for i in yuejian:
if (len(i) > 1):
flag = 1
if(flag == 1):#将集合分解开,逐个取其与其他集合的并集
simple = yuejian[0]
nosimple = deepcopy(yuejian)
i=0
while (i < len(nosimple)):
if(len(nosimple[i]) == 1):
simple = simple | nosimple[i]
nosimple.pop(i)
else:
i = i + 1
for i in range(len(nosimple)):
nosimple[i] = list(nosimple[i])
simple = list(simple)
for i in range(len(nosimple)):
for j in range(len(nosimple[i])):
simple_temp = deepcopy(simple)
simple_temp.append(nosimple[i][j])
result.append(simple_temp)
else:
simple = yuejian[0]
for i in yuejian:
simple = simple | i#如果只有单元素,则将取其与其他集合的并集
result.append(list(simple))
print(result)
#约简矩阵的各属性的样本值
matrix_new = []
for i in range(len(result)):
matrix_new.append([])
for i in range(len(result)):
for j in range(len(result[i])):
for k in range(len(attribute)):
if(result[i][j] == attribute[k]):
matrix_new[i].append(list(matrix_T[k]))
#输出
for i in range(len(matrix_new)):
print('------------------------------------')
print('序号 ',end='')
for j in range(len(result[i])):
print(result[i][j],'',end='')
print(' 归类:买计算机?')
for j in range(len(matrix_new[0][0])):
print(j+1,end = ' ')
for k in range(len(result[i])):
print(matrix_new[i][k][j], end = ' ')
print(' ',matrix[j][number_attribute])
if __name__ == '__main__':
path = 'data.xlsx'
# 读取数据
matrix = read_excel(path)
#deal(matrix)
divide(matrix)
依赖度约简代码如下:
from copy import deepcopy
import numpy as np
import pandas as pd
import xlrd
from pprint import pprint
from itertools import combinations, permutations
import random
#import 决策函数
def basic_set(df):
basic = {}
for i in df.drop_duplicates().values.tolist():
basic[str(i)] = []
for j, k in enumerate(df.values.tolist()):
if k == i:
basic[str(i)].append(j)
return basic
def divide():
path = 'data.xlsx'
global matrix,mistake
matrix = read_excel(path)
len_attribute = len(matrix[0])-1
matrix_delete = []
#决策表分解
mistake = []
for j in range(len(matrix)):
for k in range(j,len(matrix)):
if ((matrix[j][0:len_attribute] == matrix[k][0:len_attribute]).all() and matrix[j][len_attribute] != matrix[k][len_attribute]):
matrix_delete.append(list(matrix[j]))
matrix_delete.append(list(matrix[k]))
matrix = np.delete(matrix,k,axis=0)
matrix = np.delete(matrix,j,axis=0)
mistake.append(j)
mistake.append(k)
if(len(matrix_delete)):
print('矛盾:',matrix_delete)
else:
print('不存在矛盾数据!')
print('-------------------------------------------')
if(len(matrix)):
print('完全一致表:')
pprint(matrix)
else:
print('不存在完全一致表:')
if(len(matrix_delete)):
print('完全不一致表:')
print(matrix_delete)
def intersection_2(someone_excel):
x_list = someone_excel[0]
y_list = someone_excel[1]
#print(x_list)
#print(y_list)
x_set = [[]]*len(x_list)
for i in range(len(x_list)):
x_set[i] = set(x_list[i])
y_set = [[]]*len(y_list)
for i in range(len(y_list)):
y_set[i] = set(y_list[i])
a = []
for i in range(len(x_list)):
for j in range(len(y_list)):
if(x_set[i] & y_set[j]):
a.append(x_set[i] & y_set[j])
return a
def intersection(excel_temp):
if (len(excel_temp)>1):
a = intersection_2([excel_temp[0],excel_temp[1]])
for k in range(2,len(excel_temp)):
a = intersection([a,excel_temp[k]])
else:
a = excel_temp[0]
return a
# 收集属性依赖性
def dependence_degree(x_list):
count = 0
for i in x_list:
for j in y_basic_list:
if(set(i) <= set(j)):
count = count + len(i)
degree = round(count/len(x_data),4)
return degree
def yilaidu_fun(k):
excel_temp = list(combinations(excel,k))#排列组合数
title_temp = list(combinations(title,k))
for i in range(len(title_temp)):
excel_temp[i] = list(excel_temp[i])
title_temp[i] = list(title_temp[i])
#print('title_temp:',title_temp)
#print(excel_temp)
a = []
for i in range(len(excel_temp)):
temp = intersection(excel_temp[i])
#print(temp)
print(title_temp[i],end=' ')
print('依赖度:',dependence_degree(temp))
if (dependence_degree(temp) == 1):
a.append(set(title_temp[i]))
#print(a)
return a
def deal(data):
data = data.dropna(axis=0, how='any')
for i in sorted(mistake , reverse=True):
data.drop(data.index[i], inplace=True)
#使用pandas的loc来读取并把各属性值赋给变量(loc通过行标签索引数据)
age_data = data.loc[:, 'C1']
age_basic_list = sorted([v for k, v in basic_set(age_data).items() ])
#print('age:',age_basic_list)
income_data = data.loc[:, 'C2']
income_basic_list = sorted([v for k, v in basic_set(income_data).items()])
#print('income:',income_basic_list)
student_data = data.loc[:, 'C3']
student_basic_list = sorted([v for k, v in basic_set(student_data).items() ])
#print('student_data',student_data)
credit_data = data.loc[:, 'C4']
credit_basic_list = sorted([v for k, v in basic_set(credit_data).items()])
#print('student',credit_basic_list)
global x_data,y_data,y_basic_list,excel
x_data = data.drop(['judge'], axis=1)
y_data = data.loc[:, 'judge']
# 决策属性基本集
y_basic_list = sorted([v for k, v in basic_set(y_data).items() ])
#print(y_basic_list)
excel = []
excel.append(age_basic_list)
excel.append(income_basic_list)
excel.append(student_basic_list)
excel.append(credit_basic_list)
#print(excel)
yilaidu = []
for i in range(1,len(matrix)+1):
yilaidu.extend(yilaidu_fun(i))
print('依赖度为1的属性有:',yilaidu)
#print(yilaidu)
#约简
i=0
j=0
k=len(yilaidu)#k=6
for i in range(k):
for j in range(k):
if(yilaidu[i] > yilaidu[j]):#i更大,应该删除i
yilaidu[i] = yilaidu[j]
#去重
yilaidu_new = []
for i in yilaidu:
if i not in yilaidu_new:
yilaidu_new.append(i)
for i in range(len(yilaidu_new)):
yilaidu_new[i] = sorted(list(yilaidu_new[i]))
result = yilaidu_new
#各约简属性的属性值
matrix_new = []
for i in range(len(result)):
matrix_new.append([])
for i in range(len(result)):
for j in range(len(result[i])):
for k in range(len(title)):
if(result[i][j] == title[k]):
matrix_new[i].append(list(matrix_T[k]))
for i in range(len(matrix_new)):
print('------------------------------------')
print('序号 ',end='')
for j in range(len(result[i])):
print(result[i][j],'',end='')
print('归类:买计算机?')
for j in range(len(matrix_new[0][0])):
print(j+1,end=' ')
for k in range(len(result[i])):
print(matrix_new[i][k][j], end = ' ')
print(' ',matrix[j][len(matrix[0])-1])
if(result == []):
print(' 年龄 收入 学生 信誉 归类:买计算机?')
print(matrix)
def read_excel(path):
#打开excel
x_matrix = []
workbook = xlrd.open_workbook(path,'r')
table = workbook.sheets()[0]
for rown in range(1,table.nrows):
x_matrix.append(table.row_values(rown))
x_matrix = np.array(x_matrix)
#print(x_matrix)
return x_matrix
def main():
#读取文件数据
data = pd.read_csv(filepath_or_buffer='data.CSV',encoding='unicode_escape')
divide()
global matrix_T
matrix_T = matrix.T
len = data.iloc[:,0].size
#数据集
arr = data.iloc[0:len]
global title
title= ['年龄','收入','学生','信誉']
deal(arr)
if __name__ == '__main__':
main()
测试表格如下:
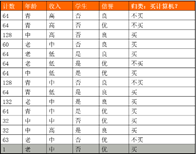
python不确定性计算之粗糙集属性约简的更多相关文章
- 【机器学习】粗糙集属性约简算法与mRMR算法的本质区别
1. 粗糙集属性约简算法仅仅选出属性重要度大的条件加入约减中,没有考虑约简中条件属性相互之间的冗余性,得到的约简往往不是都必要的,即含有冗余属性. 2. mRMR算法则除了考虑特征与类别之间的相关性, ...
- 【机器学习】粗糙集属性约简—Attribute Reduction
介绍 RoughSets算法是一种比较新颖的算法,粗糙集理论对于数据的挖掘方面提供了一个新的概念和研究方法.本篇文章我不会去介绍令人厌烦的学术概念,就是简单的聊聊RoughSets算法的作用,直观上做 ...
- python不确定性计算之模糊动态聚类实验
模糊动态聚类实验 本实验所采用的模糊聚类分析方法是基于模糊关系上的模糊聚类法,也称为系统聚类分析法,可分为三步: 第一步:数据标准化,建立模糊矩阵 第二步:建立模糊相似矩阵 第三步:聚类 本程序读取E ...
- Python TF-IDF计算100份文档关键词权重
上一篇博文中,我们使用结巴分词对文档进行分词处理,但分词所得结果并不是每个词语都是有意义的(即该词对文档的内容贡献少),那么如何来判断词语对文档的重要度呢,这里介绍一种方法:TF-IDF. 一,TF- ...
- Python科学计算之Pandas
Reference: http://mp.weixin.qq.com/s?src=3×tamp=1474979163&ver=1&signature=wnZn1UtW ...
- Python在计算内存时应该注意的问题?
我之前的一篇文章,带大家揭晓了 Python 在给内置对象分配内存时的 5 个奇怪而有趣的小秘密.文中使用了sys.getsizeof()来计算内存,但是用这个方法计算时,可能会出现意料不到的问题. ...
- Python科学计算库Numpy
Python科学计算库Numpy NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库. 1.简 ...
- python中类的三种属性
python中的类有三种属性:字段.方法.特性 字段又分为动态字段和静态字段 类 class Province: #静态字段 memo = 'listen' #动态字段 def __init__(se ...
- windows下安装python科学计算环境,numpy scipy scikit ,matplotlib等
安装matplotlib: pip install matplotlib 背景: 目的:要用Python下的DBSCAN聚类算法. scikit-learn 是一个基于SciPy和Numpy的开源机器 ...
随机推荐
- [原创] RestartPC64-中文版v1.0.0.9
原来发布的RestartPC-中文版和英文版v1.0.0.5,在PE64下无效.所以重新编译了64位版的RestartPC64-中文版v1.0.0.9,可以在PE64下面.正常Win64系统下面重启关 ...
- 我与Apache DolphinScheduler社区的故事
我与DolphinScheduler社区的故事 Apache DolphinScheduler 是一个开源的分布式去中心化.易扩展的可视化DAG大数据调度系统. 于2017年在易观数科立项,2019年 ...
- Luogu5104 红包发红包 (期望)
曾几何时有人说概率期望easy... 显然,期望是\(\frac{w}{2^n}\) #include <iostream> #include <cstdio> #includ ...
- Mybatis介绍、使用IDEA快速入门
1. Mybatis概念 MyBatis 是一款优秀的持久层框架,用于简化 JDBC 开发 JavaEE三层架构:表现层.业务层.持久层 JDBC 与 MyBatis 对比: MyBatis 本是 A ...
- HCIA-Datacom 3.4 实验四:实现VLAN间通信实验
实验介绍: 划分VLAN后,不同VLAN的用户间不能二层互访,这样能起到隔离广播的作用.但实际应用中,不同VLAN的用户又常有互访的需求,此时就需要实现不同VLAN的用户互访,简称VLAN间互访.华为 ...
- 聊天机器人框架Rasa资源整理
Rasa是一个主流的构建对话机器人的开源框架,它的优点是几乎覆盖了对话系统的所有功能,并且每个模块都有很好的可扩展性.参考文献收集了一些Rasa相关的开源项目和优质文章. 一.Rasa介绍 1.R ...
- JZM 的套题(暴力,DP)
J Z M \rm JZM JZM 即将奔赴 N O I \rm NOI NOI 考场,为了让同学们赶上自己的千分之一水平,刻意出了两道水题给同学们练练. 1.曾经的代码 J Z M \rm JZM ...
- 2019 CSP-S Ⅱ 游记
day0(试机) 第零天,重新打了一遍头文件和读优,熟悉了一下就匆匆走了. day1 T1一看到先把二分打了,然后发现long long要爆,好慌 主要是基础知识不够扎实,不知道unsigned lo ...
- 一种比css_scoped和css_module更优雅的避免css命名冲突小妙招
css_scoped 与 css_module 我们知道,简单的class名称容易造成css命名重复,比如你定义一个class: <style> .main { float: left; ...
- python自动化测试系列教程
随着互联网产品更新迭代加快,Web 开发和测试的需求也越来越大.很难想象,如果阿里的双 11.京东的 618,这些庞大繁杂的系统,由工程师们一个个手动测试,将会是一个怎样费时费力.成本巨大的工程. 也 ...
