算法设计（动态规划应用实验报告）实现基于贪婪技术思想的Prim算法、Dijkstra算法

一、名称

动态规划法应用

二、目的

1.贪婪技术的基本思想；
2.学会运用贪婪技术解决实际设计应用中碰到的问题。

三、要求

1．实现基于贪婪技术思想的Prim算法；
2．实现基于贪婪技术思想的Dijkstra算法。

四、内容

1．实现基于贪婪技术思想的Prim算法

1.1、Prim算法的伪代码描述

算法 Prim(G)
//构造最小生成树的Prim算法
//输入：加权连通图G<V,E>
//输出：E（T），组成G的最小生成树的边的集合
V(t)←{V0}  //可以用任意顶点来初始化树的顶点集合
Er←◎（集合空）
  For i←1 to |V|-1 do
在所有的边（v,u）中，求权重最小的边e*=(v*,u*),
使得v在Vt中而V-Vt中
V←VtU{u*}
Et←ErU{e*}
Return Er

2.2、Prim算法的源代码实现

package com.zyz.four;
import java.util.*;
public class Primel {
    static int MAX = Integer.MAX_VALUE;
    public static void main(String[] args) {
        int[][] map = new int[][]{
                {0, 10, MAX, MAX, MAX, 11, MAX, MAX, MAX},
                {10, 0, 18, MAX, MAX, MAX, 16, MAX, 12},
                {MAX, MAX, 0, 22, MAX, MAX, MAX, MAX, 8},
                {MAX, MAX, 22, 0, 20, MAX, MAX, 16, 21},
                {MAX, MAX, MAX, 20, 0, 26, MAX, 7, MAX},
                {11, MAX, MAX, MAX, 26, 0, 17, MAX, MAX},
                {MAX, 16, MAX, MAX, MAX, 17, 0, 19, MAX},
                {MAX, MAX, MAX, 16, 7, MAX, 19, 0, MAX},
                {MAX, 12, 8, 21, MAX, MAX, MAX, MAX, 0}};
        prim(map, map.length);
    }
    public static void prim(int[][] graph, int n) {
        char[] c = new char[]{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'E', 'F'};
        int[] lowcost = new int[n];  //到新集合的最小权
        int[] mid = new int[n];//存取前驱结点
        List<Character> list = new ArrayList<Character>();//用来存储加入结点的顺序
        int i, j, min, minid, sum = 0;
        //初始化辅助数组
        for (i = 1; i < n; i++) {
            lowcost[i] = graph[0][i];
            mid[i] = 0;
        }
        list.add(c[0]);
        //一共需要加入n-1个点
        for (i = 1; i < n; i++) {
            min = MAX;
            minid = 0;
            //每次找到距离集合最近的点
            for (j = 1; j < n; j++) {
                if (lowcost[j] != 0 && lowcost[j] < min) {
                    min = lowcost[j];
                    minid = j;
                }
            }
            if (minid == 0) return;
            list.add(c[minid]);
            lowcost[minid] = 0;
            sum += min;
            System.out.println(c[mid[minid]] + "到" + c[minid] + " 权值：" + min);
            //加入该点后，更新其它点到集合的距离
            for (j = 1; j < n; j++) {
                if (lowcost[j] != 0 && lowcost[j] > graph[minid][j]) {
                    lowcost[j] = graph[minid][j];
                    mid[j] = minid;
                }
            }
        }
        System.out.println("sum:" + sum);
    }
}

2.3、Prim算法的时间效率分析

时间效率：Tn=O（n*n）,在每一遍|V|-1次迭代中，就要遍历实现优先队列的数组，来查找并删除距离最小的顶点，如果有必要，在更新余下顶点的优先级。

2．实现基于贪婪技术思想的Dijkstra算法

2.1、Dijkstra算法的伪代码描述

算法 Dijkstra（G，s）
//单起点最短路径的Dijkstra算法
//输入：具非权重加权连通图G=<V,E>以及它的顶点s
//输出：对于V中的每个顶点v来说，从s到v的最短路径的长度d
//以及路径上的倒数第二个顶点Pv
Initialize(Q)//将顶点优先从队列初始化为空
For V中每一个顶点v
  dr←无穷大；Pv←null
insert(Q,v,dv)//初始化优先队列中顶点的优先级
ds←0;Decrease(Q,s,ds)//将s的优先级更新为ds
V(r) ←空集
For i←0 to |V|-1 do
  u* ←DeleteMin(Q) //删除优先级最小的元素
Vr←VrU{u*}
   For V-Vr中每一个和u*相邻的顶点u do
if du*+w(u*,u)<du
  du←du*+w(u*,u);pu du*+w(u*,u)u*
Decrease(Q,u,du)

2.2、Dijkstra算法的源代码实现

package com.zyz.four;
public class Dijkstra {
    /*
     * 参数adjMatrix:为图的权重矩阵，权值为-1的两个顶点表示不能直接相连
     * 函数功能：返回顶点0到其它所有顶点的最短距离，其中顶点0到顶点0的最短距离为0
     */
    public int[] getShortestPaths(int[][] adjMatrix) {
        int[] result = new int[adjMatrix.length];   //用于存放顶点0到其它顶点的最短距离
        boolean[] used = new boolean[adjMatrix.length];  //用于判断顶点是否被遍历
        used[0] = true;  //表示顶点0已被遍历
        for(int i = 1;i < adjMatrix.length;i++) {
            result[i] = adjMatrix[0][i];
            used[i] = false;
        }
        for(int i = 1;i < adjMatrix.length;i++) {
            int min = Integer.MAX_VALUE;    //用于暂时存放顶点0到i的最短距离，初始化为Integer型最大值
            int k = 0;
            for(int j = 1;j < adjMatrix.length;j++) {  //找到顶点0到其它顶点中距离最小的一个顶点
                if(!used[j] && result[j] != -1 && min > result[j]) {
                    min = result[j];
                    k = j;
                }
            }
            used[k] = true;    //将距离最小的顶点，记为已遍历
            for(int j = 1;j < adjMatrix.length;j++) {  //然后，将顶点0到其它顶点的距离与加入中间顶点k之后的距离进行比较，更新最短距离
                if(!used[j]) {  //当顶点j未被遍历时
                    //首先，顶点k到顶点j要能通行；这时，当顶点0到顶点j的距离大于顶点0到k再到j的距离或者顶点0无法直接到达顶点j时，更新顶点0到顶点j的最短距离
                    if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1))
                        result[j] = min + adjMatrix[k][j];
                }
            }
        }
        return result;
    }
    public static void main(String[] args) {
        Dijkstra test = new Dijkstra();
        int[][] adjMatrix = {{0,6,3,-1,-1,-1},
                {6,0,2,5,-1,-1},
                {3,2,0,3,4,-1},
                {-1,5,3,0,2,3},
                {-1,-1,4,2,0,5},
                {-1,-1,-1,3,5,0}};
        int[] result = test.getShortestPaths(adjMatrix);
        System.out.println("顶点0到图中所有顶点之间的最短距离为：");
        for(int i = 0;i < result.length;i++)
            System.out.print(result[i]+" ");
    }
}

2.3、Dijkstra算法的时间效率分析

Dijkstra复杂度是O(N^2)，用权重矩阵表示，优先队列用无序数组来实现。

3、运行结果

3.1、Dijkstra算法的测试用例结果截图

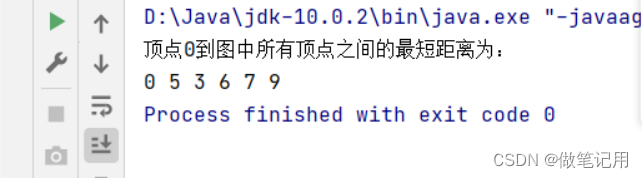
3.2、Prim算法的测试用例结果截图

4、小结

在实验的过程中，我对贪婪技术的基本思想有了更加深入的了解。学会使用动态规划的目的，将问题从小的方面开始解决，逐步向解决整个问题靠近。通过本次实验、我了解到基于贪婪技术思想的Prim算法、Dijkstra算法基本原理。掌握了基本的使用方法、能够运用这种思路解决生活中的实际问题。