【编程学习】MATLAB

目录

• 一、MATLAB基础
  • 1. 学会完成MATLAB的安装与启动
    • 1.1 软件包下载
    • 1.2 安装步骤
  • 2. 矩阵的基本操作与运算
    • 2.1 矩阵的简单输入与操作
    • 2.2 矩阵的基本运算
      • 2.2.1 算术运算
      • 2.2.2 关系运算
      • 2.2.3 逻辑运算：
    • 2.3 矩阵分析
      • 2.3.1 矩阵的转置与旋转
      • 2.3.2 矩阵的翻转
      • 2.3.3 三角阵提取
      • 2.3.4 矩阵的逆与伪逆
      • 2.3.5 方阵的行列式
      • 2.3.6 矩阵的秩与迹
      • 2.3.7 矩阵的特征值与特征向量
      • 2.3.8 实例求解
• 二、MATLAB开头命令
• 三、linspace函数的用法
• 四、continue、break和return语句
• 五、随机数产生函数用法
• 六、min()和max()
• 七、sum()用法
• 八、fmincon()

一、MATLAB基础

1. 学会完成MATLAB的安装与启动

MATLAB（矩阵实验室）是由美国MathWorks公司出品的商业数学软件，这是一款可专业分析数据的软件，软件的功能性十分强大，新版matlab 2018a增强各项功能的特性，如对图形、数据导入和导出及语言和编程进行了增强，更新了实时编辑器的交互式图形，增强了硬件支持等，让各类数学或者科研人员可以轻松地进行计算和分析等操作。MATLAB安装步骤如下：

1.1 软件包下载

Matlab R2018a（64位）下载链接：

https://pan.baidu.com/s/1nBeHrPZFwyDrtiQGXPR0dA

提取密码：ywge

安装前须知：

• 安装全程须断开电脑网络，否则安装不成功；

• Matlab 2018a的安装包必须使用虚拟光驱加载，推荐使用ULtraISO，千万不要解压进行安装；

• Matlab2018a适用于WIN7/8/10（64位）系统；

• Matlab 2018a推荐电脑配置：内存4G+，处理器酷睿I5+。

1.2 安装步骤

1. 使用“百度网盘客户端”下载Matlab 2018a软件安装包和Crack破解文件到电脑磁盘里，注意：Matlab 2018a安装包为两个iso格式文件‘

2. 安装前先断开电脑网络，然后找到R2018a_win64_dvd1.iso，鼠标右击选择【装载】（WIN10系统自带虚拟光驱，所以可以直接打开.iso文件；WIN7/8系统加载.iso文件需要另外安装虚拟光驱，可安装ULtraISO）；

3. 在弹出的窗口内找到setup.exe，鼠标右击选择【以管理员身份运行】；

4. 勾选“使用文件安装密钥”，然后点击【下一步】；

5. 许可协议界面，勾选“是”，然后点击【下一步】；

6. 输入安装密钥：09806-07443-53955-64350-21751-41297，然后点击【下一步】；

7. 选择安装文件夹，默认安装在C盘，因软件占用磁盘空间12G+，建议点击【浏览】更改软件安装位置，注意：安装路径文件夹名称均不能出现中文字符！可软件安装在D盘Matlab2018a文件夹下，设置好后点击【下一步】；

8. 去除第一条产品的勾选，放心，你一般不会用到的！然后点击【下一步】；

9. 勾选“桌面”和“开始菜单”创建快捷方式，然后点击【下一步】；

10. 默认，点击【安装】；

11. 安装进度条达59%时，弹出窗口提示：弹出DVD1并插入DVD2以继续，先不要点击“确定”，也不要关闭，先把它放在一边；

12. 下面开始装载第二个.iso文件，在装载新的.iso文件一定要先弹出之前加载的.iso文件，否则无法继续安装，双击桌面“此电脑”图标进入文件资源管理界面，找到之前加载的虚拟光驱，鼠标右击选择【弹出】；

13. 返回初始软件安装包，然后找到R2018a_win64_dvd2.iso，鼠标右击选择【装载】；

14. 点击安装界面中【确定】继续安装；

15. 安装完成后弹出产品配置说明界面，默认，点击【下一步】；

16. 安装完成，点击【完成】，安装结束后请勿直接打开软件，后续还须进行破解；

17. 下面开始破解，返回初始安装文件夹，将安装包里的R2018a_Win64_Crack.zip解压，打开解压后的文件如图所示：

18. 在解压后的文件里将License_standalone.lic复制到安装目录中Licenses文件夹里，例如安装路径位是D:\Matlab2018a，所以复制到D:\Matlab2018a\ Licenses\文件夹下；

19. 打开Crack文件内的R2018a\bin\win64文件夹，将文件夹里面的netapi32.dll文件复制并粘贴到安装目录中win64文件夹下，例如安装路径位是D:\Matlab2018a，所以复制到D:\Matlab2018a\bin\win64文件夹下;

20. 破解完成，双击桌面Matlab 2018a图标打开软件即可正常使用；

    界面如下图1所示：

    

2. 矩阵的基本操作与运算

2.1 矩阵的简单输入与操作

• MATLAB以m×n的形式保存矩阵，其中m是行数，n是列数，特别地，一个1×1矩阵是一个标量；1×n矩阵是一个行向量，m×1矩阵是一个列向量；矩阵的全部元素可以是实数，也可以是复数；方括号“[]”表示一个矩阵，空格或逗号把相邻列元素分开，分号把相邻行分开；大矩阵可用多行语句输入，用回车符代替分号来区分矩阵的行。

例如输入：

---

%行向量的输入一种方式，空格隔开

a = [1 2 3 4]

%行向量的输入另一种方式，逗号隔开（行向量=数组）

a1 = [1,2,3,4]

%列向量的输入

b = [1;2;3;4]

%矩阵的输入

c = [1 2 3;2 3 4;3 4 5]

---

结果如下：

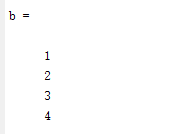
• 数组一般包括向量和矩阵，一维数组即向量（vector），二维数组即矩阵（matrix）。冒号是MATLAB中的一个重要字符，其基本使用格式为：s1:s2:s3，其中，s1为起始值，s2为步长，s3为终止值。若s2的指为负数，则要求s1大于s3，否则结果为空向量；若s2不写，则取默认值1。

例如：

---

• 二维数组子数组进行标识和寻访的最常见格式如下：

​ 全下标法：

​ A(r,c)：它由A的“r指定行和c指定列”的元素组成；

​ A(r,:)：它由A的“r指定行”和“全部列”上的元素组成；

​ A(:,c) 它由A的“全部行”和“c指定列”上的元素组成；

​ 单下标法：

​ A( ：“单下标全元素”寻访由A各列按自左到右的次序，首位相接的一维列数组；

​ A(s)：单下标寻访，生成s指定的一维数组；

例如输入：

---

---

结果如下：

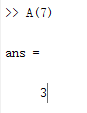
• 常用产生特殊矩阵的如下函数：

输入	生成形式
rand(m n)	随机矩阵，元素都是0到1之间
randn(m n)	正态分布的随机矩阵
zeros(m n)	零矩阵
ones(m,n)	全部元素都为1的矩阵
compan(A)	矩阵A的伴随矩阵
bankel(m,n)	Hankel矩阵
invhilb(n)	n维逆Hilbert矩阵
magic(n)	n维Magic矩阵
toeplitz(m,n)	Toeplitz矩阵
wilkinson(n)	n维wilkinscn特征值测试矩阵
handamard(n)	n维Handamard矩阵
hilb(n)	n维Hilbert矩阵
kron(A,B)	Kronecker 张量积
pascal(n)	n维Pascal矩阵
vander(A)	由矩阵A产生vandermonde矩阵

例如输入：

---

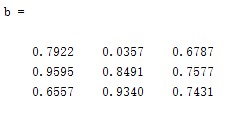
a = eye(3,3)

b = rand(3,3)

c = ones(3,3)

d = zeros(3,3)

---

结果如下：

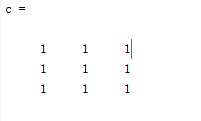
操作矩阵的常用函数如下:

输入	作用
size(x)	用于求矩阵x的大小
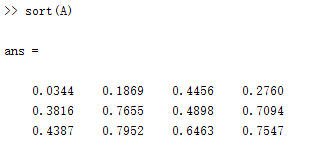
sort(x)	可对x进行升序排序，x为向量、数组、矩阵等等
find(x)	用来返回向量或者矩阵中不为0的元素的索引
numl(A)	返回数组A中元素的个数
ismember(A,B)	集合成员判断B中成员和A成员是否相等，相等的位置用1，否则用0
findstr(A,B)，strfind(A,B)	在A，B中较长的字符串中查找较短的字符串出现的次数
setdiff(A,B)	返回在数组A中有B中没有的值，并将其结果向量以升序排序返回
intersect(A,B)	返回A和B共有的数据，不包含重复项，将其结果按升序排序
unique(x)	去掉矩阵x中重复的值并按升序排序

例如输入：

---

>> A = rand(3,4)

A =

0.0344 0.7655 0.4898 0.7094

0.4387 0.7952 0.4456 0.7547

0.3816 0.1869 0.6463 0.2760

---

结果如下：

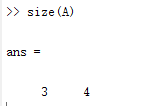
2.2 矩阵的基本运算

2.2.1 算术运算

MATLAB的基本算术运算有：＋(加)、－(减)、*(乘)、/(右除)、\(左除)、^(乘方)、’(转置)。运算是在矩阵意义下进行的，单个数据的算术运算只是一种特例。

矩阵加减运算：假定有两个矩阵A和B，则可以由A+B和A-B实现矩阵的加减运算。运算规则是：若A和B矩阵的维数相同，则可以执行矩阵的加减运算，A和B矩阵的相应元素相加减。如果A与B的维数不相同，则MATLAB将给出错误信息，提示用户两个矩阵的维数不匹配。

例如输入：

---

---

结果如下：

矩阵乘法运算：假定有两个矩阵A和B，若A为m*n矩阵，B为n*p矩阵，则C=A*B为m*p矩阵。

例如输入：

---

---

结果如下：

矩阵除法运算：在MATLAB中，有两种矩阵除法运算：\和/，分别表示左除和右除。如果A矩阵是非奇异方阵，则A\B和B/A运算可以实现。A\B等效于A的逆左乘B矩阵，也就是inv(A)*B，而B/A等效于A矩阵的逆右乘B矩阵，也就是B*inv(A)。对于含有标量的运算，两种除法运算的结果相同。对于矩阵来说，左除和右除表示两种不同的除数矩阵和被除数矩阵的关系，一般A\B≠B/A。

例如输入：

---

A = [1:3;4:6;7:9]

B = [2:4;6:8;10:12]

C = A\B

D = B/A

---

结果如下：

矩阵的乘方运算：一个矩阵的乘方运算可以表示成A^x，要求A为方阵，x为标量。

例如输入：

---

---

结果如下：

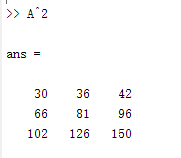
矩阵的点运算：在MATLAB中 有一种特殊的运算，因为其运算符是在有关算术运算符前面加点，所以叫点运算。点运算符有.*、./、.\和.^。两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵的维参数相同。

例如输入：

---

---

结果如下：

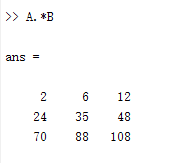
2.2.2 关系运算

MATLAB提供了6种关系运算符：<(小于)、<=(小于或等于)、>(大于)、>=(大于或等于)、==(等于)、~=(不等于)。关系运算符的运算法则为：

(1) 当两个比较量是标量时，直接比较两数的大小。若关系成立，关系表达式结果为1，否则为0；

(2) 当参与比较的量是两个维数相同的矩阵时，比较是对两矩阵相同位置的元素按标量关系运算规则逐个进行，并给出元素比较结果。最终的关系运算的结果是一个维数与原矩阵相同的矩阵，它的元素由0或1组成；

(3) 当参与比较的一个是标量，而另一个是矩阵时，则把标量与矩阵的每一个元素按标量关系运算规则逐个比较，并给出元素比较结果。最终的关系运算的结果是一个维数与原矩阵相同的矩阵，它的元素由0或1组成。

例如输入：

---

>> A = [1:3;4:6;7:9]

B = [2:4;6:8;10:12]

---

结果如下：

2.2.3 逻辑运算：

MATLAB提供了3种逻辑运算符：&(与)、|(或)和~(非)。

逻辑运算的运算法则为：

(1) 在逻辑运算中，确认非零元素为真，用1表示，零元素为假，用0表示；

(2) 设参与逻辑运算的是两个标量a和b，那么，a&b，a,b全为非零时，运算结果为1，否则为0；a|b，a,b中只要有一个非零，运算结果为1；~a，当a是零时，运算结果为，；当a非零时，运算结果为0。

(3) 若参与逻辑运算的是两个同维矩阵，那么运算将对矩阵相同位置上的元素按标量规则逐个进行。最终运算结果是一个与原矩阵同维的矩阵，其元素由1或0组成；

(4) 若参与逻辑运算的一个是标量，一个是矩阵，那么运算将在标量与矩阵中的每个元素之间按标量规则逐个进行。最终运算结果是一个与矩阵同维的矩阵，其元素由1或0组成；

(5) 逻辑非是单目运算符，也服从矩阵运算规则；

(6) 在算术、关系、逻辑运算中，算术运算优先级最高，逻辑运算优先级最低。

例如输入：

---

---

结果如下：

2.3 矩阵分析

2.3.1 矩阵的转置与旋转

矩阵的转置：转置运算符是单撇号(’)。例如：

---

---

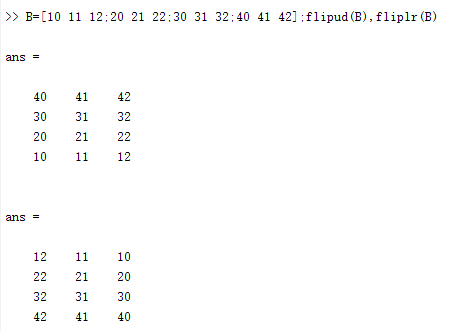
2.3.2 矩阵的翻转

MATLAB提供了一些矩阵翻转的特殊命令，如rot90(A)表示将矩阵A逆时针旋转90度，flipud(A)表示将A矩阵上下翻转，fliplr(A)表示将A矩阵左右翻转等。例如：

---

2.3.3 三角阵提取

三角阵分为上三角阵和下三角阵，所谓上三角阵，即矩阵的对角线以下的元素全为0的一种矩阵，而下三角阵则是对角线以上的元素全为0的一种矩阵。

上三角矩阵 求矩阵A的上三角阵的MATLAB函数是triu(A)。triu(A)函数也有另一种形式triu(A,k)，其功能是求矩阵A的第k条对角线以上的元素。

下三角矩阵在MATLAB中，提取矩阵A的下三角矩阵的函数是tril(A)和tril(A,k)，其用法与提取上三角矩阵的函数triu(A)和triu(A,k)完全相同。例如：

---

2.3.4 矩阵的逆与伪逆

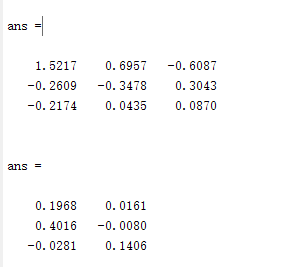
矩阵的逆：对于一个方阵A，如果存在一个与其同阶的方阵B，使得：AB=BA=I(I为单位矩阵)，则称B为A的逆矩阵，当然，A也是B的逆矩阵。求方阵A的逆矩阵可调用函数inv(A)。

矩阵的伪逆：如果矩阵A不是一个方阵，或者A是一个非满秩的方阵时，矩阵A没有逆矩阵，但可以找到一个与A的转置矩阵A’同型的矩阵B，使得：ABA=A，BAB=B 此时称矩阵B为矩阵A的伪逆，也称为广义逆矩阵。在MATLAB中，求一个矩阵伪逆的函数是pinv(A)。

例如：

---

2.3.5 方阵的行列式

把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为矩阵所对应的行列式的值。在MATLAB中，求方阵A所对应的行列式的值的函数是det(A)。

例如：

---

2.3.6 矩阵的秩与迹

矩阵的秩 矩阵线性无关的行数与列数称为矩阵的秩。在MATLAB中，求矩阵秩的函数是rank(A)。

矩阵的迹矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。在MATLAB中，求矩阵的迹的函数是trace(A)。

例如：

---

2.3.7 矩阵的特征值与特征向量

在MATLAB中，计算矩阵A的特征值和特征向量的函数是eig(A)，常用的调用格式有3种：

• E=eig(A)：求矩阵A的全部特征值，构成向量E。

• [V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。

• [V,D]=eig(A,’nobalance’)：与第2种格式类似，但第2种格式中先对A作相似变换后求矩阵A的特征值和特征向量，而格式3直接求矩阵A的特征值和特征向量。

例如：

---

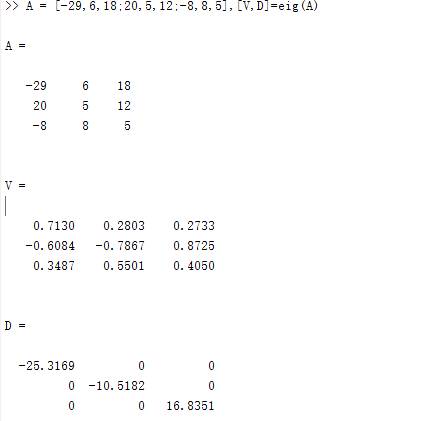
2.3.8 实例求解

（1）求矩阵A的特征值与特征向量

以《矩阵分析》教材P54，题1-23（1）为例，结果如下：

---

二、MATLAB开头命令

命令	作用
clc	清除命令窗口的内容，对工作环境中的全部变量无任何影响
clear	清除工作空间的所有变量
clear all	清除工作空间的所有变量，函数，和MEX文件
close	闭当前的Figure窗口
close all	关闭所有的Figure窗口
tic	用来保存当前时间，而后使用toc来记录程序完成时间

常规开头：

clc

clear all

close all

三、linspace函数的用法

语法

y = linspace(x1,x2)

y = linspace(x1,x2,n)

---

说明

• y = linspace(x1,x2) 返回包含 x1 和 x2 之间的 100 个等间距点的行向量。

• y = linspace(x1,x2,n) 生成 n 个点。这些点的间距为 (x2-x1)/(n-1)。

= linspace 类似于冒号运算符“:”，但可以直接控制点数并始终包括端点。

• “linspace”名称中的“lin”指示生成线性间距值而不是同级函数 logspace，后者会生成对数间距值。

---

创建一个由区间 [-5,5] 中的 100 个等距点组成的向量。

y = linspace(-5,5);

---

包含指定数量的值的向量

创建一个由区间 [-5,5] 中的 7 个等距点组成的向量。

---

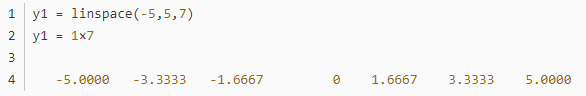
由均匀分布的复数组成的向量

创建一个复数向量，包含介于1+2i和10+10i之间的8个等距点。

---

输入参数

点区间，指定为数值标量对组。

x1和x2定义linspace生成点的区间。x1和x2可以是实数或复数x2可以大于或小于x1。如果x2比x1小，则向量包含递减的值。

n——点的数目，指定为实数标量。

如果n为1，则linspace返回x2。

如果n为零或负数，则linspace返回1×0空矩阵。

如果 n 不是整数，则 linspace 向下舍入并返回 floor(n) 个点。

四、continue、break和return语句

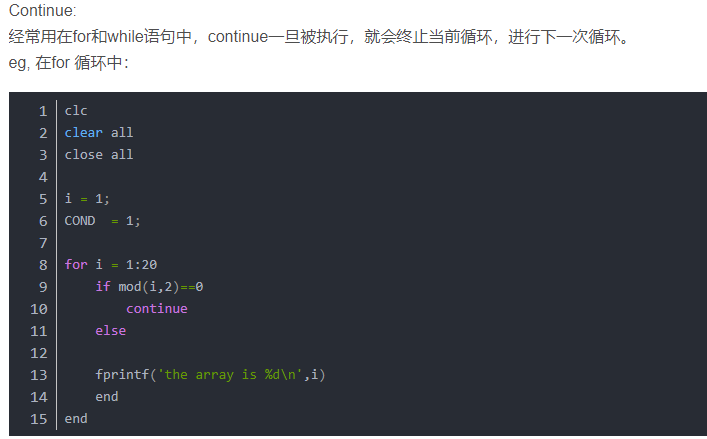
continue 将控制权传递到 for 或 while 循环的下一迭代。它跳过当前迭代的循环体中剩余的任何语句。程序继续从下一迭代执行。

continue 仅在调用它的循环的主体中起作用。在嵌套循环中，continue 仅跳过循环所发生的循环体内的剩余语句。

**

---

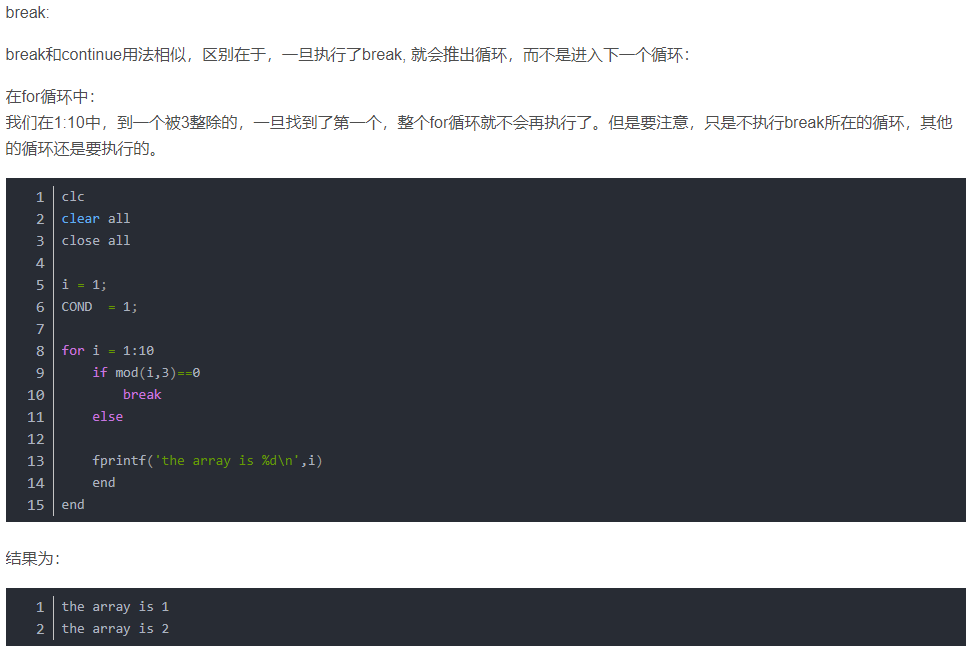
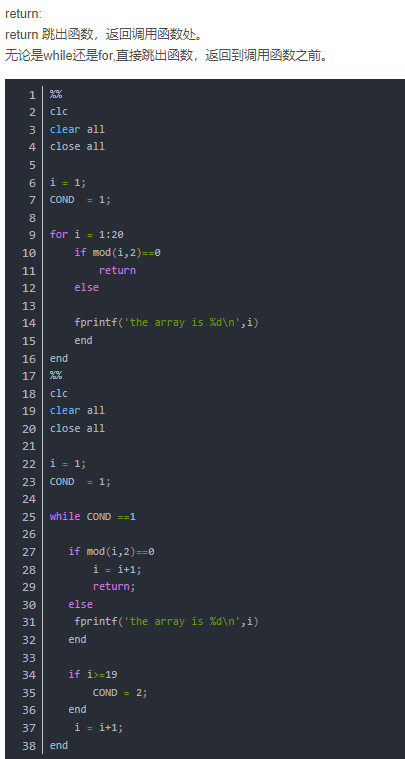
五、随机数产生函数用法

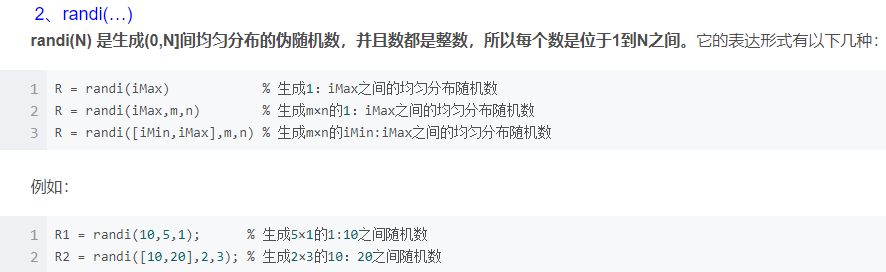
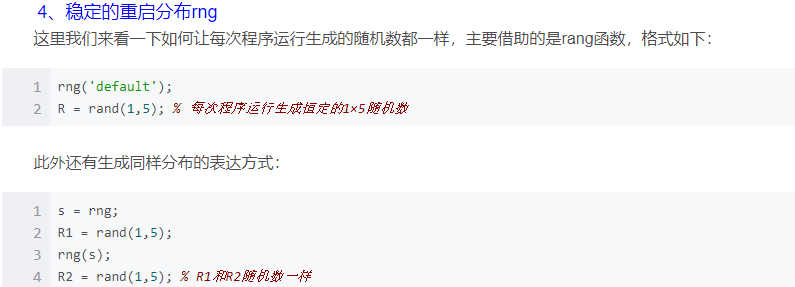
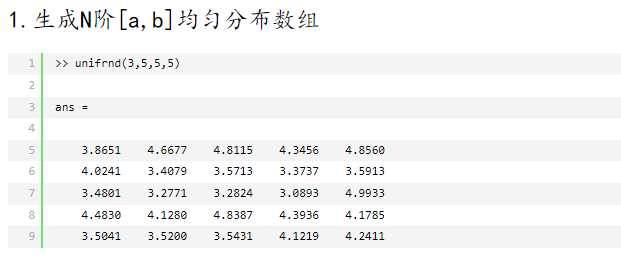
Matlab随机数生成函数：

函数	生成类型
betarnd	贝塔分布的随机数生成器
binornd	二项分布的随机数生成器
chi2rnd	卡方分布的随机数生成器
exprnd	指数分布的随机数生成器
frnd	f分布的随机数生成器
gamrnd	伽玛分布的随机数生成器
geornd	几何分布的随机数生成器
hygernd	超几何分布的随机数生成器
lognrnd	对数正态分布的随机数生成器
nbinrnd	负二项分布的随机数生成器
ncfrnd	非中心f分布的随机数生成器
nctrnd	非中心t分布的随机数生成器
ncx2rnd	非中心卡方分布的随机数生成器
normrnd	正态(高斯)分布的随机数生成器
poissrnd	泊松分布的随机数生成器
raylrnd	瑞利分布的随机数生成器
trnd	学生氏t分布的随机数生成器
unidrnd	离散均匀分布的随机数生成器
unifrnd	连续均匀分布的随机数生成器
weibrnd	威布尔分布的随机数生成器

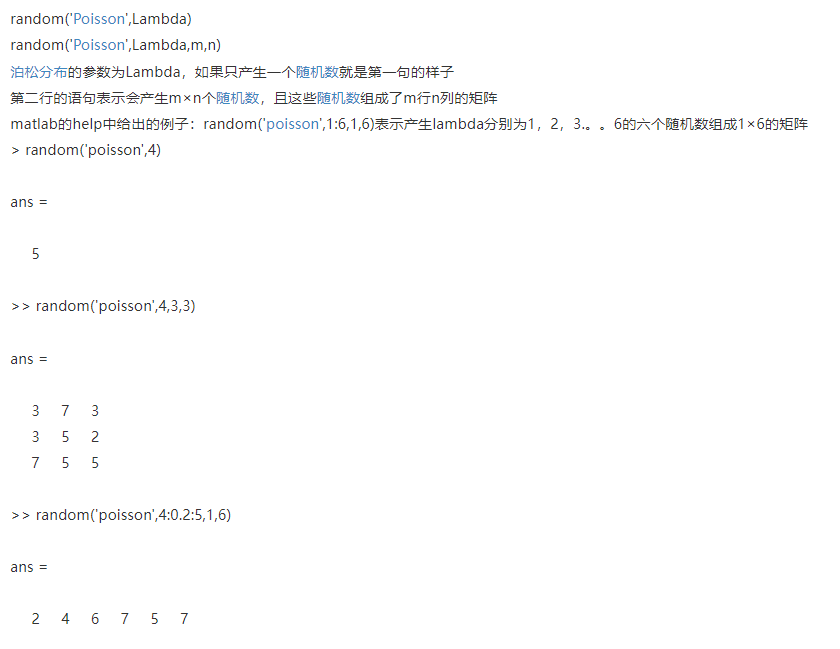
六、min()和max()

七、sum()用法

八、fmincon()

x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)

求解标准型：

function f = myfun(x);

f = 优化目标函数;

function [c,ceq] = nonlcon(x)

c = 非线性不等式约束

ceq = 非线性等式约束

x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@nonlcon)

x0为优化初值

例：

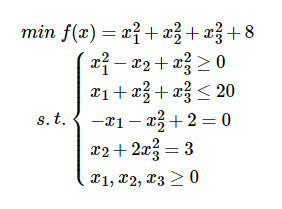
function f = myfun(x);

f=x(1).^2+x(2).^2+x(3).^2+8;

function [c,ceq]= mycon(x);

c=[-x(1).^2+x(2)-x(3).^2 %标准型是≤，本例是≥，所以对变量取反

x(1)+x(2).^2+x(3).^3-20];

ceq=[-x(1)-x(2).^2+2

x(2)+2*x(3).^2-3];

[x,result]=fmincon(@myfun,rand(3,1),[ ],[ ],[ ],[ ],zeros(3,1),[ ],' mycon ')

输出结果：x1=0.5522，x2=1.2033，x3=0.9478

result = 10.651