C组合方案

递归实现组合型枚举

从 1∼n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

输入格式

两个整数 n,m ,在同一行用空格隔开。

输出格式

按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

数据范围

n>0 ,

0≤m≤n ,

n+(n−m)≤25

输入样例：

5 3

输出样例：

1 2 3

1 2 4

1 2 5

1 3 4

1 3 5

1 4 5

2 3 4

2 3 5

2 4 5

3 4 5

图解

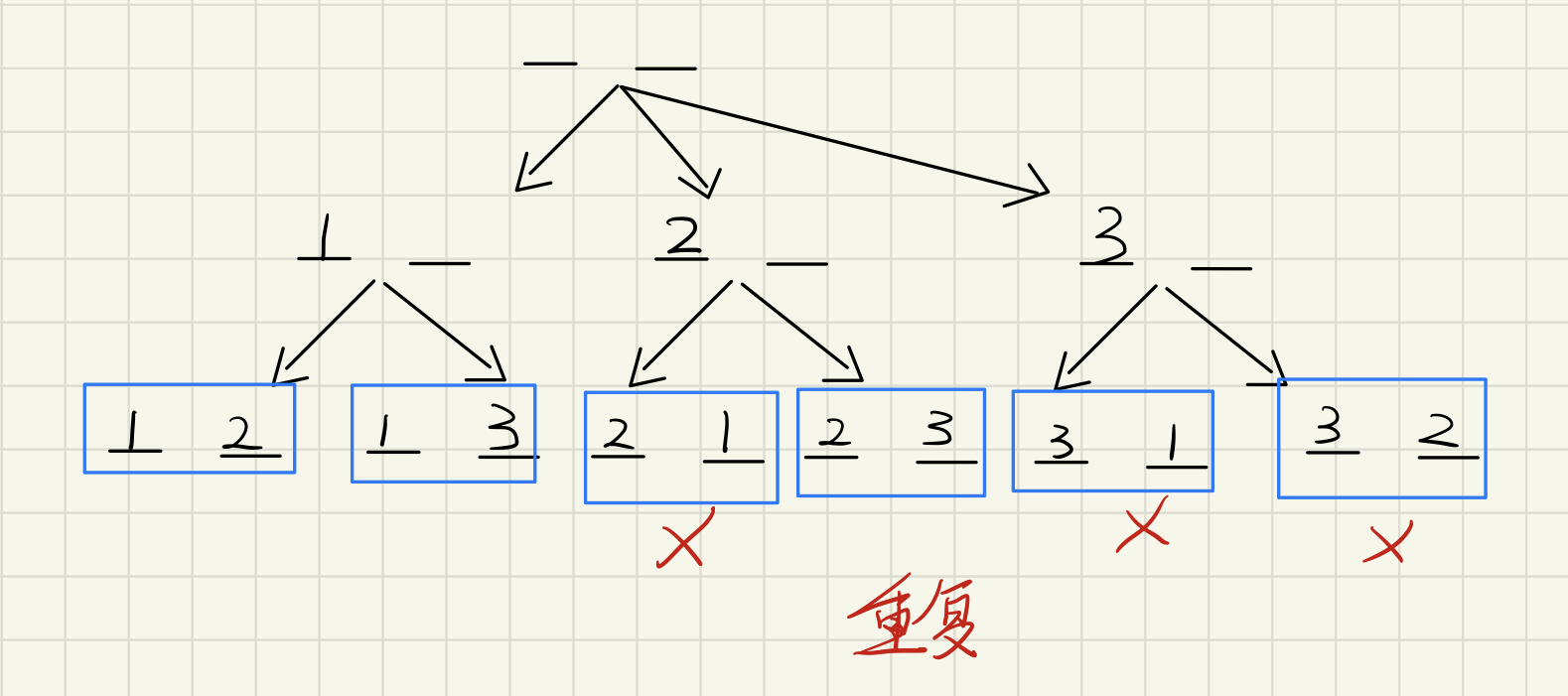
在排列基础上维护正序即可确保方案不重复

Code

点击查看代码

#include<iostream>
using namespace std;
int n,m;
bool st[20];		//是否选过
int ways[20];		//保存方案

void dfs(int x){	//选到第x位//前一位是start
    if(x > m){		//选到第m+1位，即得到一种方案
        for(int i = 1; i <= m; i ++ ){		//输出方案
            cout << ways[i] << " ";
        }
        puts("");
        return ;		//注意要退出
    }

    for(int i = ways[x - 1] + 1; i <= n; i ++ ){			//从前一位的下一位开始枚举枚举每一位
        if(!st[i]){				//如果没选过
            st[i] = 1;
            ways[x] = i;		//选i
            dfs(x + 1);			//选下一位
			ways[x] = 0;		//恢复现场
            st[i] = 0;
        }
    }
}

int main(){
    cin >> n >> m;
    dfs(1);			//从第一位开始选//前一位是0
}

优化

1. 方法：剪枝
2. 优化前：160ms左右，优化后：40ms左右

点击查看代码

#include<iostream>
using namespace std;
int n,m;
bool st[20];
int ways[20];

void dfs(int x){
	if(ways[x - 1] + (m - x + 1) > n)return;  //优化
	//ways[x - 1]表示上一位枚举的是什么
	//m - x + 1标志还有多少位要枚举
	//ways[x - 1] + (m - x + 1) > n表示如果全部正序枚举完后所需要的最大数大于n提前退出递归
    if(x > m){
        for(int i = 1; i <= m; i ++ ){
            cout << ways[i] << " ";
        }
        puts("");
        return ;
    }

    for(int i = ways[x - 1] + 1; i <= n; i ++ ){
        if(!st[i]){
            st[i] = 1;
            ways[x] = i;
            dfs(x + 1);
			ways[x] = 0;
            st[i] = 0;
        }
    }
}

int main(){
    cin >> n >> m;
    dfs(1);
}