Linux操作系统（2）：组管理和权限管理

组管理和权限管理

Outline
1、查看文件所有者：ls -ahl
2、更改文件或目录权限命令：chmod
3、更改文件或目录所有者命令：chown
4、更改文件或目录所属组命令：chgrp

---

1）组管理

在 linux 中的每个用户必须属于一个组，不能独立于组外。在 linux 中每个文件有所有者、所在组、其它组的概念。
1) 所有者
2) 所在组
3) 其它组
4) 改变用户所在的组

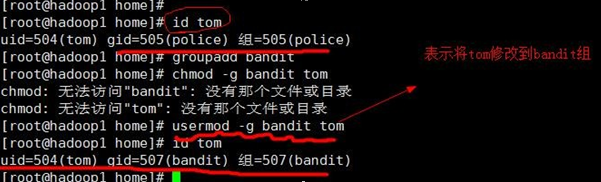
①    ls -ahl   ：查看文件的所有者

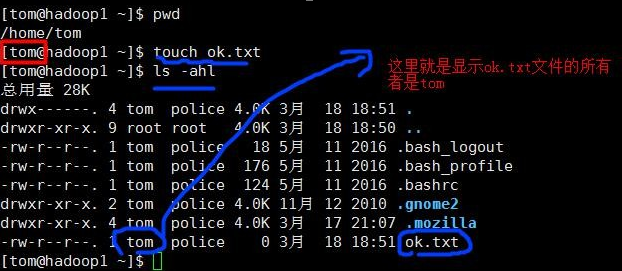
② chown  用户名  文件名   ：修改文件的所有者

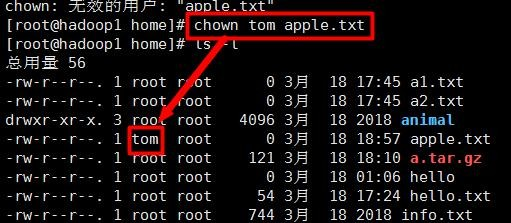
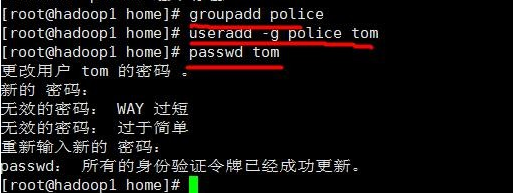
③ groupadd 组 名   ：组的创建

④  chgrp 组名 文件名    ：修改文件所在的组

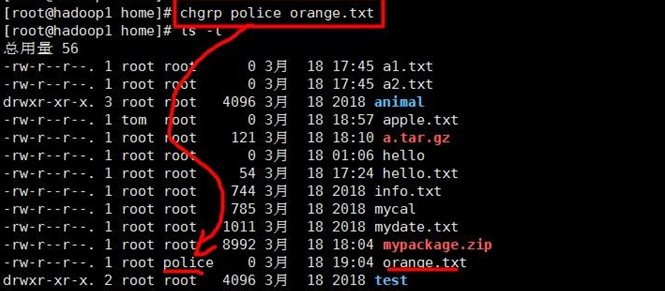
⑤   usermod   –g    组名  用户名   ：改变用户所在组

---

2）权限管理

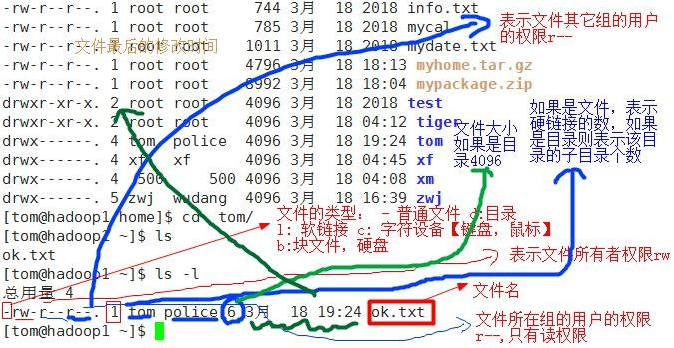
ls    -l 中显示的内容如下：
- rwx rw- r-- 1 root root 1213 Feb 2 09:39 abc
0-9 位说明
1)第 0 位确定文件类型(d, - , l , c , b)
2)第 1-3 位确定所有者（该文件的所有者）拥有该文件的权限。---User
3)第 4-6 位确定所属组（同用户组的）拥有该文件的权限，---Group
4)第 7-9 位确定其他用户拥有该文件的权限 ---Other

rwx 作用到文件
　　1) [ r  ]代表可读(read):  可以读取,查看
　　2) [ w ]代表可写(write): 可以修改,但是不代表可以删除该文件,删除一个文件的前提条件是对该文件所在的目录有写权限，才能删除该文件.
　　3) [ x  ]代表可执行(execute):可以被执行
rwx 作用到目录
　　1) [ r ]代表可读(read):  可以读取，ls 查看目录内容
　　2) [ w ]代表可写(write):  可以修改,目录内创建+删除+重命名目录
　　3) [ x ]代表可执行(execute):可以进入该目录

　　可用数字表示为: r=4,w=2,x=1  因此 rwx=4+2+1=7

⑥ 通过 chmod 指令，可以修改文件或者目录的权限

方式1：+ 、-、=  变更权限

　　u:所有者  g:所有组  o:其他人  a:所有人 (u、g、o 的总和)
　　1) chmod u=rwx,g=rx,o=x 文件目录名
　　2) chmod o+w 文件目录名
　　3) chmod a-x 文件目录名

　　例子1：给 abc 文件 的所有者读写执行的权限，给所在组读执行权限，给其它组读执行权限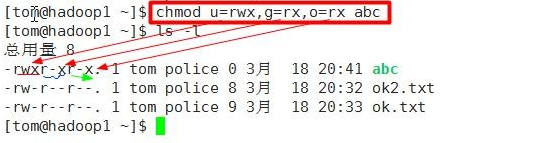

　　例子2：给 abc 文件的所有者除去执行的权限，增加组写的权限

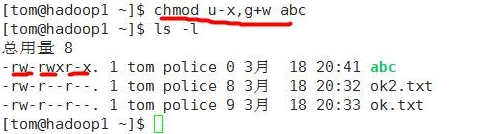
方式2：通过数字变更权限

　　规则：r=4 w=2 x=1  ,rwx=4+2+1=7

chmod u=rwx,g=rx,o=x   文件目录名

相当于       chmod 751  文件目录名

　　例子1：将  /home/abc.txt 文件的权限修改成       rwx r-x r-x, 使用给数字的方式实现

rwx = 4+2+1 = 7
r-x = 4+1=5
r-x = 4+1 =5
指令：chmod 755 /home/abc.txt

⑦ chown  修改文件所有者

chown    newowner    file             改变文件的所有者
chown    newowner:newgroup    file    改变用户的所有者和所有组
-R    如果是目录 则使其下所有子文件或目录递归生效

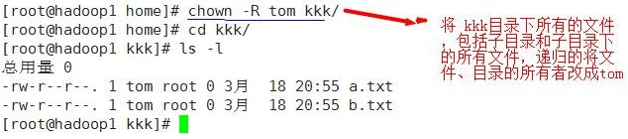
⑧ chgrp  修改文件所在组

chgrp newgroup file    改变文件的所有组